Геометрическая алгебра

Геометрическая алгебра — историческое построение алгебры, изложенное во второй книге «Начал» Евклида (III век до н. э.), где операции определялись непосредственно для геометрических величин, а теоремы доказывались геометрическими построениями. Другими словами, алгебра античных математиков не только выросла из проблем геометрии, но и полностью строилась на геометрической основе[1].

Не следует путать с Алгебраическая геометрия.

Например, произведение числовых величин определялось[2] как прямоугольник со сторонами и .

Примеры

Утверждение теоремы Пифагора можно интерпретировать как алгебраическое равенство, а можно как равенство площадей квадратов, построенных на катетах и квадрата, построенного на гипотенузе. Второй способ является примером подхода геометрической алгебры.

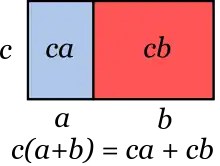
Геометрическое представление распределительного закона

Распределительный закон античные математики представляли как равенство площади прямоугольника сумме площадей двух прямоугольников, получаемых разрезанием исходного параллельно одной из сторон (см. рисунок).

История

В IV веке до н. э. пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, то есть их отношение () нельзя выразить ни натуральным числом, ни дробью. Однако других числовых объектов, кроме натуральных чисел, античные математики не признавали, даже дробь рассматривалась ими не как число, а как соотношение (пропорция)[3].

Найти выход сумел в IV веке до н. э. Евдокс Книдский — он ввёл, наряду с числами, понятие геометрических величин (длин, площадей, объёмов). Для однородных величин были определены арифметические операции, аналогичные числовым. Теория Евдокса была изложена Евклидом в пятой книге его «Начал», и она использовалась в Европе до XVII века. Теоремы о числах Евклиду приходилось отдельно передоказывать для величин, да и арифметика величин была существенно беднее, чем числовая — хотя бы потому, что касалась только однородных величин[4][5].

Критика

В Новое время выяснилось, что построение числовой алгебры на основе геометрии было ошибкой. Например, с точки зрения геометрии выражения и даже не имели геометрического истолкования (не определена физическая размерность величины-результата) и поэтому не имели смысла; то же относится к отрицательным числам[6].

Начиная с «Геометрии» Декарта (1637), европейские математики пошли иным путём — они создали аналитическую геометрию, которая вместо сведе́ния алгебры к геометрии выполняет сведе́ние геометрии к алгебре, и этот путь оказался намного более плодотворным. Чтобы сделать это возможным, Декарт расширил понятие числа — оно вобрало все вещественные числа, включая иррациональные, и является отвлечённым, то есть отделено от геометрии[7]. Отдельное понятие геометрической величины тогда становится излишним. Алгебраизация геометрии позволила, кроме того, обнаружить общие черты в геометрических задачах, которые казались совершенно независимыми[8].

Некоторые историки существование геометрической алгебры подвергли сомнению. Например, Шабтай Унгуру считал, что поскольку история математики писалась не историками, а математиками, они в своих реконструкциях исходили из того, что математика в своей сущности неизменна, и поэтому при изложении истории они свободно употребляли идеи и термины современной математики.

Примечания
  1. Никифоровский, Фрейман, 1976, с. 5.
  2. Цейтен, 1932, с. 42—43.
  3. История математики, том I, 1970, с. 72—74.
  4. Колмогоров А. Н. Величина // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 1.
  5. История математики, том I, 1970, с. 78.
  6. Башмакова И. Г. Лекции по истории математики в Древней Греции // Историко-математические исследования. — М.: Физматгиз, 1958. — № 11. — С. 309—323.
  7. Юшкевич А. П. Декарт и математика, 1938, с. 279—282.
  8. Scott, J. F. The scientific work of René Descartes. — New York: Garland, 1987. — ISBN 0824046722.

Литература
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — 352 с.
  • Никифоровский В. А., Фрейман Л. С. Рождение новой математики. — М.: Наука, 1976. — 199 с. — (Из истории мировой культуры).
  • Цейтен Г. Г. История математики в древности и в средние века. — М.—Л.: ГТТИ, 1932. — 230 с.
  • Юшкевич А. П. Декарт и математика // Декарт Р. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М—Л.: Гостехиздат, 1938. — С. 257—294. — 297 с. — (Классики естествознания).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.