Вложение Татта

Вложение Татта (барицентричное вложение) простого вершинно 3-связного планарного графа — вложение без пересечений с рёбрами в виде отрезков с дополнительными свойствами, что внешняя грань имеет выпуклый многоугольник в качестве границы и что каждая внутренняя вершина является геометрическим центром соседей. Если внешний многоугольник фиксирован, это условие на внутренние вершины определяет их положения однозначно как решение системы линейных уравнений. Решение уравнений даёт планарное вложение. Теорема Татта «о резиновой укладке» утверждает, что в единственном решении никогда нет пересечений рёбер и, что более строго, что любая грань получающегося планарного вложения выпукла[1]. Вложение называется «резиновым», поскольку такое вложение может быть найдено как равновесное положение системы пружин или резиновых ремней, представляющих рёбра графа.

Пример
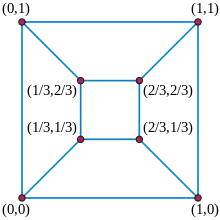
Вложение Татта графа куба. Внешние четыре вершины фиксированы в углах единичного квадрата, а оставшиеся вершины являются геометрическим центром соседних вершин.

Пусть G — граф куба. Зафиксируем (выбрав одну из четырёхугольных граней в качестве внешней грани) четыре вершины внешней грани в углах единичного квадрата, координаты x и y которого являются комбинациями нулей и единиц. Оставшиеся четыре вершины тогда располагаются в четырёх точках, координаты x и y которых являются комбинациями 1/3 и 2/3, как показано на рисунке. Результат — вложение Татта. Для каждой внутренней вершины v этого вложения соседние три вершины имеют три значения координат (как x, так и y), одно равно координате v, одно меньше, а другое больше на 1/3. В среднем получаем значение координаты самой точки v.

Система линейных уравнений

Условие, что вершина v имеет среднее значение координат соседей, можно выразить в виде двух линейных уравнений, одно для координаты x точки v, другое для координаты y. Для графа с n вершинами, h которых фиксированы в вершинах внешней грани, имеется два уравнения и две неизвестные (координаты) для каждой внутренней вершины. Таким образом, получаем систему линейных уравнений с 2(n − h) уравнениями с 2(n − h) неизвестными, решением которого будет вложение Татта. Как показал Татт[2], для вершинно 3-связных планарных графов эта система не вырождена. Поэтому система будет иметь единственное решение и (с фиксированной внешней гранью) граф будет единственным вложением Татта. Это вложение можно найти за полиномиальное время путём решения системы уравнений, например, используя последовательное исключение переменных[3].

Представление многогранников

По теореме Штайница 3-связные планарные графы, для которых применяется теорема Татта «о резиновой укладке», совпадают с полиэдральными графами, графами, образованными вершинами и рёбрами выпуклого многогранника. Согласно методу Максвелла-Кремона двумерное вложение планарного графа образует проекцию трёхмерного выпуклого многогранника тогда и только тогда, когда вложение имеет равновесное напряжение, распределение сил для каждого ребра (в обоих концах рёбер в противоположных направлениях, параллельных рёбрам), так что силы в каждой вершине уравновешиваются. Для вложения Татта распределение сил для каждого ребра пропорционально длине ребра (подобно резинке) уравновешивает силы во всех внутренних точках, но не в вершинах внешнего многоугольника. Если внешний многоугольник является треугольником, можно назначить отталкивающие силы на трёх внешних рёбрах, которые уравновесят силы в вершинах внешнего треугольника. Таким образом, вложение Татта может быть использовано для поиска диаграмм Шлегеля любого выпуклого многогранника. Для любого 3-связного планарного графа G либо сам граф G, либо его двойственный имеет треугольник, так что получаем многогранное представление графа G или его двойственного. В случае, когда двойственный граф имеет треугольную грань, полярное сопряжение даёт многогранное представление самого графа G[3].

Обобщения

Гортлер, Готсман и Тёрстон[4] доказали результаты, аналогичные теореме Татта «о резиновой укладке», для вложений графов в тор[5].

Чилакамарри, Дин и Литман[6] исследовали трёхмерное вложение графов четырёхмерных многогранников, образованное тем же методом, что и в методе вложения Татта — выбираем одну внешнюю фасету многогранника в качестве внешней грани трёхмерного вложения и фиксируем положение вершин в трёхмерном пространстве. Остальные вершины многогранника можно двигать, а рёбра заменим пружинами (или резиновыми шнурами). Теперь найдём конфигурацию системы пружин с минимальной энергией. Как они показали, система уравнений, полученная таким образом, снова будет невырожденной, но остаётся неясным, при каких условиях этот метод найдёт вложение, в котором все грани многогранника будут выпуклыми[7].

Связанные результаты

Факт, что любой простой планарный граф может быть нарисован с прямолинейными рёбрами, называется теоремой Фари[8]. Теорема Татта «о резиновой укладке» доказывает это для 3-связных планарных графов, но теорема Фари верна для любых планарных графов независимо от связности. Применение теоремы Татта для графов, не являющихся 3-связными, может привести к вырождению, при котором подграфы данного графа сливаются в точку или отрезок. Тем не менее, любой планарный граф можно нарисовать с помощью вложения Татта путём добавления дополнительных рёбер, чтобы сделать его 3-связным, затем рисуется 3-связный граф и из него удаляются лишние рёбра.

Граф вершинно k-связен (но не обязательно планарен) тогда и только тогда, когда он имеет вложение в (k −1)-мерное пространство, в котором любой набор из k вершин располагается в вершинах симплекса, а для любой оставшейся вершины v выпуклая оболочка соседей вершины v имеет полную размерность и v располагается внутри этой оболочки. Если такое вложение существует, его можно найти, зафиксировав положение k вершин и решив систему уравнений. Решение располагает каждую вершину в место, являющееся средним положением соседей, точно так же, как при планарном вложении Татта[9].

В методе конечных элементов при построении сетки сглаживание Лапласа является общим методом постобработки полученной сетки для улучшения качества[10] и особенно это популярно для четырёхугольных сеток, для которых другие методы, такие как алгоритм Ллойда для сглаживания треугольных сеток, менее применимы. В этом методе каждая вершина в направлении среднего положения позиций соседей, но это движение осуществляется за малое число итераций, чтобы избежать большого искажения размеров элементов, или (в случае невыпуклой области сетки) получения спутанных непланарных сеток.

Силовые методы укладки графов продолжают быть популярным методом визуализации графов, но эти системы обычно используют более сложные системы сил, которые комбинируют силы притяжения рёбер графа (как во вложении Татта) с отталкивающими силами между двумя произвольными парами вершин. Эти дополнительные силы могут дать системе много локальных устойчивых конфигураций, а не одну глобальную, как во вложении Татта[11].

Примечания
  1. Tutte, 1963, с. 743–767.
  2. Tutte, 1963.
  3. Rote, 2012, с. 238–241.
  4. Gortler, Gotsman, Thurston, 2006.
  5. Gortler, Gotsman, Thurston, 2006, с. 83–112.
  6. Chilakamarri, Dean, Littman, 1995.
  7. Chilakamarri, Dean, Littman, 1995, с. 129–140.
  8. О связи между теоремами Татта и Фари и истории переоткрытия теоремы Фари см. книгу Фелснера (Felsner 2012).
  9. Linial, Lovász, Wigderson, 1988, с. 91–102.
  10. Herrmann, 1976, с. 749–907.
  11. Kobourov, 2012.

Литература
  • Steven J. Gortler, Craig Gotsman, Dylan Thurston. Discrete one-forms on meshes and applications to 3D mesh parameterization // Computer Aided Geometric Design. — 2006. — Т. 23, вып. 2. — С. 83–112. — doi:10.1016/j.cagd.2005.05.002.
  • Günter Rote. Graph Drawing: 19th International Symposium, GD 2011, Eindhoven, The Netherlands, September 21–23, 2011, Revised Selected Papers. — Springer, 2012. — Т. 7034. — С. 238–241. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-25878-7_23.
  • Kiran Chilakamarri, Nathaniel Dean, Michael Littman. Three-dimensional Tutte embedding // Congressus Numerantium, Proceedings of the Twenty-sixth Southeastern International Conference on Combinatorics, Graph Theory and Computing (Boca Raton, FL, 1995). — 1995. — Т. 107. — С. 129–140.
  • Stefan Felsner. Geometric Graphs and Arrangements: Some Chapters from Combinatorial Geometry. — Springer, 2012. — С. 37. — (Advanced Lectures in Mathematics). — ISBN 9783322803030.
  • N. Linial, L. Lovász, A. Wigderson. Rubber bands, convex embeddings and graph connectivity // Combinatorica. — 1988. — Т. 8, вып. 1. — С. 91–102. — doi:10.1007/BF02122557.
  • Leonard R. Herrmann. Laplacian-isoparametric grid generation scheme // Journal of the Engineering Mechanics Division. — 1976. — Т. 102, вып. 5. — С. 749–907.
  • W. T. Tutte. How to draw a graph // Proceedings of the London Mathematical Society. — 1963. — Т. 13. — С. 743–767. — doi:10.1112/plms/s3-13.1.743.
  • Stephen G. Kobourov. Spring Embedders and Force-Directed Graph Drawing Algorithms. — 2012. — arXiv:1201.3011.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.