Бета-остов
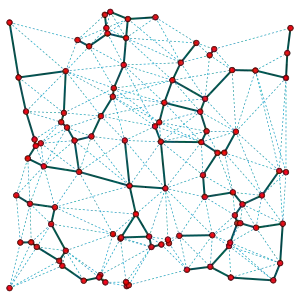
-остов, бета-остов или бета-скелет — это ориентированный граф, определённый на множестве точек на евклидовой плоскости. Две точки p and q связаны ребром, когда все углы prq меньше некоторого порога, определённого параметром .
Определение на основе окружностей
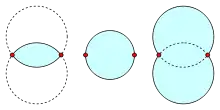
Пусть будет положительным вещественным числом, вычислим угол по формулам
Для любых двух точек p и q на плоскости пусть Rpq будет множеством точек, для которых угол prq больше . Тогда Rpq принимает вид объединения двух открытых дисков с диаметром для и и принимает форму пересечения двух открытых дисков диаметра для и . Когда две формулы дают то же самое значение, и Rpq принимает форму одного открытого диска с pq в качестве диаметра.
-остов дискретного множества S точек плоскости — это неориентированный граф, который соединяет две точки p и q ребром pq, когда Rpq не содержит точек S. То есть -остов является графом пустых пространств, определённых областями Rpq[1]. Если S содержит точку r, для которой угол prq больше , то pq не является ребром -остова. -остов состоит из тех пар pq, для которых такая точка r существует.
Определение на основе линз
Некоторые авторы используют альтернативное определение, в котором пустые области Rpq для являются не объединением двух дисков, а линзой, пересечением двух дисков с диаметрами , таких, что отрезок pq лежит на радиусах обоих дисков, так что обе точки p и q лежат на границе пересечения. Как и в случае основанного на окружностях -остова, основанный на линзах -остов имеет ребро pq, когда область Rpq пуста от других точек. Для этого альтернативного определения, граф относительных окрестностей является специальным случаем -остова с . Два определения совпадает для , а для бо́льших значений основанный на окружностях остов является подграфом основанного на линзах остова.
Одна важная разница между основанных на окружностях и основанных на линзах -остовов заключается в том, что для любого множества точек, которые не лежат на одной прямой, всегда существует достаточно большое значение , такое, что основанный на окружностях -остов является пустым графом. Для контраста, если пара точек p и q имеет свойство, что для любой точки r один из двух углов pqr и qpr тупой, то основанный на линзах -остов будет содержать ребро pq независимо от того, насколько велико значение .
История
-остова первым определили Киркпатрик и Радке[2] как масштабно инвариантый вариант альфа-формы Эдельсбруннера, Киркпатрика и Зайделя[3]. Название -остов отражает факт, что в некотором смысле -остов описывает форму множества точек таким же образом, как топологический скелет описывает форму двумерной области. Рассматривались также обобщения -остова графов, определёнными другими пустыми областями [1][4].
Свойства
Если меняется непрерывно от 0 до , основанные на окружности -остова образуют последовательность графов от полного графа до пустого графа. Специальный случай ведёт к графу Габриэля, который, как известно, содержат евклидово минимальное остовное дерево. Поэтому -остов также содержит граф Габриэля и минимальное остовное дерево, если .
Для любой постоянной построение фрактала, который напоминает сглаженную версию снежинки Коха, может быть использовано для определения последовательности точечных множеств, -остова которых являются путями произвольно большой длины в единичном квадрате. Поэтому, в отличие от тесно связанной триангуляции Делоне, -остова имеют неограниченный коэффициент растяжения и не являются геометрическими остовами[5][6][7].
Алгоритмы
Простой естественный алгоритм, который проверяет каждую тройку p, q и r на принадлежность точки r области Rpq, может построить -остов любого множества с n точками за время O(n3).
Когда , -остов (в любом определении) является подграфом графа Габриэля, который является подграфом триангуляции Делоне. Если pq является ребром триангуляции Делоне, но не является ребром -остова, то точка r, которая образует больший угол prq, может быть найдена как одна из двух точек, образующих треугольник с точками p и q в триангуляции Делоне. Поэтому для этих значений основанный на окружностях -остов для множества n точек может быть построен за время O(n log n) путём вычисления триангуляции Делоне и используя этот тест как фильтр для рёбер[4].
Для другой алгоритм Уртадо, Лиотты и Meijer[8] позволяет построить -остов за время O(n2). Никакой лучшей границы для времени в худшем случае не существует, поскольку для любого фиксированного значения , меньшего единицы, существуют множества точек в общем положении (небольшие возмущения правильного многоугольника), для которых -остов является плотным графом с квадратным числом рёбер. В тех же квадратичных временных границах можно вычислить весь -спектр (последовательность основанных на окружностях -остовов, получающихся изменением ).
Приложения
Основанный на окружностях -остов может быть использован в анализе изображений при восстановлении формы двухмерного объекта, если дано множество точек на границе объекта (вычислительный аналог головоломки «Соединить точки», где последовательность, в которой точки нужно связать, не заданы заранее как часть головоломки, а их алгоритм должен вычислить). Хотя, в общем случае, это требует выбора значения параметра , можно доказать, что выбор будет правильно восстанавливать всю границу любой гладкой поверхности и не будет создавать любое ребро, которое не принадлежит границе, так как точки генерируются достаточно плотно относительно локальной кривизны поверхности[9][10]. Однако в экспериментальных тестах меньшее значение было более эффективно для восстановления карты улиц по множеству точек, отображающих центральные линии улиц в геоинформационной системе[11]. Как обобщение техники -остова для восстановления поверхностей в трёхмерном пространстве, см. Hiyoshi (2007).
Основанные на окружностях -остова использовались для поиска графов минимальной взвешенной триангуляции множества точек — для достаточно больших значений любое ребро -остова гарантированно принадлежит минимальной взвешенной триангуляции. Если рёбра, найденные таким образом, образуют связный граф на всех точках, то оставшиеся рёбра минимальной взвешенной триангуляции могут быть найдены за полиномиальное время с помощью динамического программирования. Однако, в общем случае, задача минимальной взвешенной триангуляции является NP-трудной задачей и подмножество рёбер, найденных таким образом, может не быть связным[12][13].
-остова были также применены в обучении машин для задач геометрической классификации[14][15] и в беспроводных ad-hoc-сетях в качестве механизма контроля сложности сети путём выбора подмножества пар беспроводных станций, которые могут общаться друг с другом[16].
Примечания
- Cardinal, Collette, Langerman, 2009.
- Kirkpatrick, Radke, 1985.
- Edelsbrunner, Kirkpatrick, Seidel, 1983.
- Veltkamp, 1992.
- Eppstein, 2002.
- Bose, Devroye, Evans, Kirkpatrick, 2002.
- Wang, Li, Moaveninejad, Wang, Song, 2003.
- Hurtado, Liotta, Meijer, 2003.
- Amenta, Bern, Eppstein, 1998.
- O'Rourke, 2000.
- Radke, Flodmark, 1999.
- Keil, 1994.
- Cheng, Xu, 2001.
- Zhang, King, 2002.
- Toussaint, 2005.
- Bhardwaj, Misra, Xue, 2005.
Литература
- Nina Amenta, Marshall Bern, David Eppstein. The crust and the beta-skeleton: combinatorial curve reconstruction // Graphical Models & Image Processing. — 1998. — Т. 60/2, вып. 2. — С. 125–135. Архивировано 22 марта 2006 года..
- Manvendu Bhardwaj, Satyajayant Misra, Guoliang Xue. Workshop on High Performance Switching and Routing (HPSR 2005), Hong Kong, China. — 2005. Архивировано 7 июня 2011 года..
- Prosenjit Bose, Luc Devroye, William Evans, David G. Kirkpatrick. On the spanning ratio of Gabriel graphs and -skeletons // LATIN 2002: Theoretical Informatics. — Springer-Verlag, 2002. — Т. 2286. — С. 77–97. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-45995-2_42.
- Jean Cardinal, Sébastian Collette, Stefan Langerman. Empty region graphs // Computational Geometry Theory & Applications. — 2009. — Т. 42, вып. 3. — С. 183–195. — doi:10.1016/j.comgeo.2008.09.003.
- Siu-Wing Cheng, Yin-Feng Xu. On -skeleton as a subgraph of the minimum weight triangulation // Theoretical Computer Science. — 2001. — Т. 262, вып. 1–2. — С. 459–471. — doi:10.1016/S0304-3975(00)00318-2..
- Herbert Edelsbrunner, David G. Kirkpatrick, Raimund Seidel. On the shape of a set of points in the plane // IEEE Transactions on Information Theory. — 1983. — Т. 29, вып. 4. — С. 551–559. — doi:10.1109/TIT.1983.1056714.
- David Eppstein. Beta-skeletons have unbounded dilation // Computational Geometry Theory & Applications. — 2002. — Т. 23, вып. 1. — С. 43–52. — doi:10.1016/S0925-7721(01)00055-4. — arXiv:cs.CG/9907031..
- Hiyoshi H. Greedy beta-skeleton in three dimensions // Proc. 4th International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2007). — 2007. — С. 101–109. — doi:10.1109/ISVD.2007.27..
- Ferran Hurtado, Giuseppe Liotta, Henk Meijer. Optimal and suboptimal robust algorithms for proximity graphs // Computational Geometry Theory & Applications. — 2003. — Т. 25, вып. 1–2. — С. 35–49. — doi:10.1016/S0925-7721(02)00129-3.
- J. Mark Keil. Computing a subgraph of the minimum weight triangulation // Computational Geometry Theory & Applications. — 1994. — Т. 4, вып. 1. — С. 18–26. — doi:10.1016/0925-7721(94)90014-0..
- David G. Kirkpatrick, John D. Radke. A framework for computational morphology // Computational Geometry. — Amsterdam: North-Holland, 1985. — Т. 2. — С. 217–248. — (Machine Intelligence and Pattern Recognition)..
- Joseph O'Rourke. Computational Geometry Column 38 // SIGACT News. — 2000. — Т. 31, вып. 1. — С. 28–30. — doi:10.1145/346048.346050. — arXiv:cs.CG/0001025.
- John D. Radke, Anders Flodmark. The use of spatial decompositions for constructing street centerlines // Geographic Information Sciences. — 1999. — Т. 5, вып. 1. — С. 15–23.
- Godfried Toussaint. Geometric proximity graphs for improving nearest neighbor methods in instance-based learning and data mining // International Journal of Computational Geometry and Applications. — 2005. — Т. 15, вып. 2. — С. 101–150. — doi:10.1142/S0218195905001622.
- Remko C. Veltkamp. The γ-neighborhood graph // Computational Geometry Theory & Applications. — 1992. — Т. 1, вып. 4. — С. 227–246. — doi:10.1016/0925-7721(92)90003-B.
- Weizhao Wang, Xiang-Yang Li, Kousha Moaveninejad, Yu Wang, Wen-Zhan Song. The spanning ratio of -skeletons // Proc. 15th Canadian Conference on Computational Geometry (CCCG 2003). — 2003. — С. 35–38.
- Wan Zhang, Irwin King. Locating support vectors via -skeleton technique // Proc. Proceedings of the 9th International Conference on Neural Information Processing (ICONIP'02), Orchid Country Club, Singapore, November 18-22, 2002. — 2002. — С. 1423–1427.
