Атом гелия

Схемы термов для пара — и ортогелия с одним электроном в основном состоянии 1S и одним возбужденным электроном.

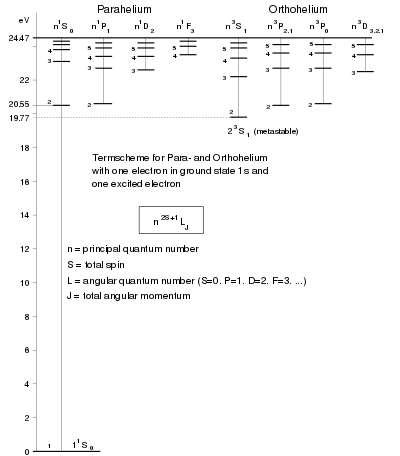
Квантово механическое описание атома гелия представляет особый интерес, потому что это самая простая многоэлектронная система, которую можно использовать для понимания концепции квантовой запутанности. Гамильтониан для атома гелия рассматривается как система трёх тел: двух электронов и ядра. После разделения движения на движение электронов с приведённой массой и движение центра масс его можно записать в виде

${\displaystyle H({\vec {r}}_{1},\,{\vec {r}}_{2})=\sum _{i=1,2}{\Bigg (}-{\frac {\hbar ^{2}}{2\mu }}\nabla _{r_{i}}^{2}-{\frac {Ze^{2}}{4\pi \epsilon _{0}r_{i}}}{\Bigg )}-{\frac {\hbar ^{2}}{M}}\nabla _{r_{1}}\cdot \nabla _{r_{2}}+{\frac {e^{2}}{4\pi \epsilon _{0}r_{12}}}}$

где ${\displaystyle \mu ={\frac {mM}{m+M}}}$ — привёдённая масса электрона относительно более массивного ядра, ${\displaystyle {\vec {r}}_{1}}$ и ${\displaystyle {\vec {r}}_{2}}$ — радиус-векторы от ядра к электронам и расстояние между электронами ${\displaystyle r_{12}=|{\vec {r_{1}}}-{\vec {r_{2}}}|}$. Заряд ядра, ${\displaystyle Z}$ равен двум для гелия. В приближении бесконечно тяжёлого ядра, ${\displaystyle M=\infty }$ получим ${\displaystyle \mu =m}$ а член ${\displaystyle {\frac {\hbar ^{2}}{M}}\nabla _{r_{1}}\cdot \nabla _{r_{2}}}$ исчезает. В атомных единицах запись гамильтониана упрощается

${\displaystyle H({\vec {r}}_{1},\,{\vec {r}}_{2})=-{\frac {1}{2}}\nabla _{r_{1}}^{2}-{\frac {1}{2}}\nabla _{r_{2}}^{2}-{\frac {Z}{r_{1}}}-{\frac {Z}{r_{2}}}+{\frac {1}{r_{12}}}.}$

Этот гамильтониан действует не в нормальном пространстве, а в шестимерном конфигурационном пространстве ${\displaystyle ({\vec {r}}_{1},\,{\vec {r}}_{2})}$. В этом приближении (приближение Паули) волновая функция это спинор второго ранга с четырьмя компонентами ${\displaystyle \psi _{ij}({\vec {r}}_{1},\,{\vec {r}}_{2})}$, где индексы ${\displaystyle i,j=\,\uparrow ,\downarrow }$ описывают проекции спинов для электронов (z-направление вверх или вниз) в некоторой координатной системе. [1] Она должна подчиняться обычному условию на норму

${\displaystyle \sum _{ij}\int d{\vec {r}}_{1}d{\vec {r}}_{2}|\psi _{ij}|^{2}=1}$.

Этот обобщённый спинор записывают в виде матрицы 2×2

${\displaystyle {\boldsymbol {\psi }}={\begin{pmatrix}\psi _{\uparrow \uparrow }&\psi _{\uparrow \downarrow }\\\psi _{\downarrow \uparrow }&\psi _{\downarrow \downarrow }\end{pmatrix}}}$

и соответственно в виде линейной комбинации в каком либо заданном базисе из черырёх ортогональных (в векторном пространстве матриц 2x2) постоянных матриц ${\displaystyle {\boldsymbol {\sigma }}_{k}^{i}}$ с коэффициентами заданными скалярными функциями ${\displaystyle \phi _{i}^{k}({\vec {r}}_{1},\,{\vec {r}}_{2})}$ в виде ${\displaystyle {\boldsymbol {\psi }}=\sum _{ik}\phi _{i}^{k}({\vec {r}}_{1},\,{\vec {r}}_{2}){\boldsymbol {\sigma }}_{k}^{i}}$. Удобный базис состоит из одной антисимметричной матрицы (с полным моментом ${\displaystyle S=0}$, для синглетного состояния)

${\displaystyle {\boldsymbol {\sigma }}_{0}^{0}={\frac {1}{\sqrt {2}}}{\begin{pmatrix}0&1\\-1&0\end{pmatrix}}={\frac {1}{\sqrt {2}}}(\uparrow \downarrow -\downarrow \uparrow )}$

и трёх симметричных матриц (с полным моментом ${\displaystyle S=1}$, для триплетного состояния)

${\displaystyle {\boldsymbol {\sigma }}_{0}^{1}={\frac {1}{\sqrt {2}}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}={\frac {1}{\sqrt {2}}}(\uparrow \downarrow +\downarrow \uparrow )}$, ${\displaystyle {\boldsymbol {\sigma }}_{1}^{1}={\begin{pmatrix}1&0\\0&0\end{pmatrix}}=\;\uparrow \uparrow }$, ${\displaystyle {\boldsymbol {\sigma }}_{-1}^{1}={\begin{pmatrix}0&0\\0&1\end{pmatrix}}=\;\downarrow \downarrow .}$

Нетрудно показать, что синглетное состояние инвариантно относительно всех вращений (скаляр), в то время как триплету сопоставлен обычный пространственный вектор ${\displaystyle (\sigma _{x},\sigma _{y},\sigma _{z})}$, с тремя компонентами

${\displaystyle \sigma _{x}={\frac {1}{\sqrt {2}}}{\begin{pmatrix}1&0\\0&-1\end{pmatrix}}}$, ${\displaystyle \sigma _{y}={\frac {i}{\sqrt {2}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}$, ${\displaystyle \sigma _{z}={\frac {1}{\sqrt {2}}}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}}$.

Поскольку всеми спин-взаимодействиями четырёх компонентов в приведённом выше (скалярном) Гамильтониане можно пренебречь (например, внешним магнитным полем, релятивистскими эффектами, как и спин-орбитальным взаимодействием), то четыре уравнения Шредингера можно решить самостоятельно. [2]

Спин появляется в задаче через принцип Паули, который для фермионов (например, электронов) требует антисимметрию волновой функции при одновременном обмене спинов и координат

${\displaystyle {\boldsymbol {\psi }}_{ij}({\vec {r}}_{1},\,{\vec {r}}_{2})=-{\boldsymbol {\psi }}_{ji}({\vec {r}}_{2},\,{\vec {r}}_{1})}$.

Парагелий соответствует синглетному состоянию ${\displaystyle {\boldsymbol {\psi }}=\phi _{0}({\vec {r}}_{1},\,{\vec {r}}_{2}){\boldsymbol {\sigma }}_{0}^{0}}$ с симметричной функцией ${\displaystyle \phi _{0}({\vec {r}}_{1},\,{\vec {r}}_{2})=\phi _{0}({\vec {r}}_{2},\,{\vec {r}}_{1})}$ и ортогелий iэто триплетное состояние ${\displaystyle {\boldsymbol {\psi }}_{m}=\phi _{1}({\vec {r}}_{1},\,{\vec {r}}_{2}){\boldsymbol {\sigma }}_{m}^{1},\;m=-1,0,1}$ с антисимметричной функцией ${\displaystyle \phi _{1}({\vec {r}}_{1},\,{\vec {r}}_{2})=-\phi _{1}({\vec {r}}_{2},\,{\vec {r}}_{1})}$. Если пренебречь электрон-электронным взаимодействием, обе пространственные функции ${\displaystyle \phi _{x},\;x=0,1}$ можно записать в виде линейной комбинации двух произвольных (ортогональных и нормированных) одноэлектронных собственных функций ${\displaystyle \varphi _{a},\varphi _{b}}$: ${\displaystyle \phi _{x}={\frac {1}{\sqrt {2}}}(\varphi _{a}({\vec {r}}_{1})\varphi _{b}({\vec {r}}_{2})\pm \varphi _{a}({\vec {r}}_{2})\varphi _{b}({\vec {r}}_{1}))}$ или для специального случая ${\displaystyle \varphi _{a}=\varphi _{b}}$ (оба электрона имеют одинаковые квантовые числа, для парагелия): ${\displaystyle \phi _{0}=\varphi _{a}({\vec {r}}_{1})\varphi _{a}({\vec {r}}_{2})}$. Полнаяэнергия (собвственное значение ${\displaystyle H}$) для всех случаев ${\displaystyle E=E_{a}+E_{b}}$ (независимо от симметрии).

Это объясняет отсутствие ${\displaystyle 1^{3}S_{1}}$ состояния (с ${\displaystyle \varphi _{a}=\varphi _{b}=\varphi _{1s}}$) для ортогелия, где следовательно ${\displaystyle 2^{3}S_{1}}$ (с ${\displaystyle \varphi _{a}=\varphi _{1s},\varphi _{b}=\varphi _{2s}}$) находится в метастабильном состоянии. (Состояние с квантовыми числами: главным квантовым числом ${\displaystyle n}$, суммарным спином ${\displaystyle S}$, угловым квантовым числом ${\displaystyle L}$ и полным угловым моментом ${\displaystyle J=|L-S|\dots L+S}$ обозначается ${\displaystyle n^{2S+1}L_{J}}$.)

Если учесть электрон-электронное взаимодействие ${\displaystyle {\frac {1}{r_{12}}}}$, то уравнение Шредингера не разделимы. Однако, если пренебречь всеми состояниями описанными выше (даже с двумя одинаковыми квантовыми числами, как ${\displaystyle 1^{1}S_{0}}$ с ${\displaystyle {\boldsymbol {\psi }}=\varphi _{1s}({\vec {r}}_{1})\varphi _{1s}({\vec {r}}_{2}){\boldsymbol {\sigma }}_{0}^{0}}$) общую волновую функцию нельзя записать как произведение одноэлектронных волновых функций: ${\displaystyle \psi _{ik}({\vec {r}}_{1},\,{\vec {r}}_{2})\neq \chi _{i}({\vec {r}}_{1})\xi _{k}({\vec {r}}_{2})}$ — волновая функция запутанная. В этом случае нельзя сказать, что частица 1 находится в состоянии 1 , а другая-в состоянии 2, и измерения нельзя произвести для одной частицы не затрагивая другую.

Тем не менее, вполне хорошее теоретическое описание атома гелия можно получить в рамках приближений Хартри — Фока и Томаса — Ферми (см. ниже).

Метод Хартри — Фока используется для различных атомных систем. Однако это только приближение, и есть более точные и эффективные методы, используемые для решения атомных систем. Задача многих тел для гелия и других электронных систем с малым числом электронов можно решить достаточно точно. Например, основное состояние гелия известно с точностью до пятнадцати цифр. В теории Хартри-Фока предполагается, что электроны движутся в потенциале, создаваемом ядром и другими электронами. Этот гамильтониан для гелия с двумя электронами можно записать как сумму гамильтонианов для каждого электрона:

${\displaystyle H=\sum _{i=1}^{2}h(i)=H_{0}+H^{\prime }}$

где невозмущенный гамильтониан равен

${\displaystyle H_{0}=-{\frac {1}{2}}\nabla _{r_{1}}^{2}-{\frac {1}{2}}\nabla _{r_{2}}^{2}-{\frac {Z}{r_{1}}}-{\frac {Z}{r_{2}}}}$

а возмущение:

${\displaystyle H'={\frac {1}{r_{12}}}}$

описывает электрон-электронное взаимодействие. H₀ — это просто сумма двух гамильтонианов для атома водорода:

${\displaystyle H_{0}={\hat {h}}_{1}+{\hat {h}}_{2}}$

где

${\displaystyle {\hat {h}}_{i}=-{\frac {1}{2}}\nabla _{r_{i}}^{2}-{\frac {Z}{r_{i}}},i=1,2}$

E_ni и ${\displaystyle \psi _{n_{i},l_{i},m_{i}}({\vec {r}}_{i})}$ соответствующие собственные собственные значения и нормированные собственные функции. Таким образом

${\displaystyle {\hat {h}}_{i}\psi _{n_{i},l_{i},m_{i}}({\vec {r_{i}}})=E_{n_{i}}\psi _{n_{i},l_{i},m_{i}}({\vec {r_{i}}})}$

где

${\displaystyle E_{n_{i}}=-{\frac {1}{2}}{\frac {Z^{2}}{n_{i}^{2}}}}$

Когда пренебрегают электрон-электронным отталкиванием, то уравнение Шредингера для пространственной части двухэлектронной волновой функции сводятся к невозмущённым уравнениям

${\displaystyle H_{0}\psi ^{(0)}({\vec {r}}_{1},{\vec {r}}_{2})=E^{(0)}\psi ^{(0)}({\vec {r}}_{1},{\vec {r}}_{2})}$

Эти уравнения развязываются и собственные функции можно записать в виде отдельных произведений водородных волновых функций:

${\displaystyle \psi ^{(0)}({\vec {r}}_{1},{\vec {r}}_{2})=\psi _{n_{1},l_{1},m_{1}}({\vec {r}}_{1})\psi _{n_{2},l_{2},m_{2}}({\vec {r}}_{2})}$

Соответствующие энергии (далее в атомных единицах):

${\displaystyle E_{n_{1},n_{2}}^{(0)}=E_{n_{1}}+E_{n_{2}}=-{\frac {Z^{2}}{2}}{\Bigg [}{\frac {1}{n_{1}^{2}}}+{\frac {1}{n_{2}^{2}}}{\Bigg ]}}$

Обратите внимание, что волновая функция

${\displaystyle \psi ^{(0)}({\vec {r}}_{2},{\vec {r}}_{1})=\psi _{n_{2},l_{2},m_{2}}({\vec {r}}_{1})\psi _{n_{1},l_{1},m_{1}}({\vec {r}}_{2})}$

Обмен электронных индексов соответствует одной и той же энергии ${\displaystyle E_{n_{1},n_{2}}^{(0)}}$. Этот конкретный случай вырождения по отношению замены электронных индексов называется обменным вырождением. Точные пространственные волновые функций двухэлектронных атомов должны быть симметричными или антисимметричными по отношению к перестановке координат ${\displaystyle {\vec {r}}_{1}}$ и ${\displaystyle {\vec {r}}_{2}}$ двух электронов. Правильная волновая функция тогда должна состоять из симметричной (+) и антисимметричной (-) линейных комбинаций:

${\displaystyle \psi _{\pm }^{(0)}({\vec {r}}_{1},{\vec {r}}_{2})={\frac {1}{\sqrt {2}}}[\psi _{n_{1},l_{1},m_{1}}({\vec {r}}_{1})\psi _{n_{2},l_{2},m_{2}}({\vec {r}}_{2})\pm \psi _{n_{2},l_{2},m_{2}}({\vec {r}}_{1})\psi _{n_{1},l_{1},m_{1}}({\vec {r}}_{2})]}$

что следует из слейтеровского детерминанта.

Множитель ${\displaystyle {\frac {1}{\sqrt {2}}}}$ нормирует ${\displaystyle \psi _{\pm }^{(0)}}$. Для того, чтобы получить эту волновую функцию в виде одного произведения одночастичных волновых функций, мы используем тот факт, что в основном состоянии ${\displaystyle n_{1}=n_{2}=1,\,l_{1}=l_{2}=0,\,m_{1}=m_{2}=0}$. Тогда ${\displaystyle \psi _{-}^{(0)}}$ исчезнет, в согласии с первоначальной формулировкой принципа Паули, в котором два электрона не могут находиться в одном состоянии. Таким образом, волновую функцию для гелия запишется в виде

${\displaystyle \psi _{0}^{(0)}({\vec {r}}_{1},{\vec {r}}_{2})=\psi _{1}({\vec {r_{1}}})\psi _{1}({\vec {r_{2}}})={\frac {Z^{3}}{\pi }}e^{-Z(r_{1}+r_{2})}}$

где ${\displaystyle \psi _{1}}$ и ${\displaystyle \psi _{2}}$ использованные волновые функции для гамильтониана атома водорода. [lower-alpha 1] Для гелия, Z = 2 и

${\displaystyle E_{0}^{(0)}=E_{n_{1}=1,\,n_{2}=1}^{(0)}=-Z^{2}{\text{ a.u.}}}$

где E${\displaystyle _{0}^{(0)}}$ = −4 а. е. что примерно −108.8 эВ, что соответствует ионизационному потенциалу V${\displaystyle _{P}^{(0)}}$ = 2 а. е. (≅54.4 эВ). Экспериментальные значения Е${\displaystyle _{0}}$ = −2.90 а. е. (≅ −79.0 эВ) и V${\displaystyle _{p}}$ = 0.90 а. е. (≅ 24.6 эВ).

Энергия, которую мы получили слишком низкая, потому что отталкивание между электронами было проигнорировано, который приводит к повышению уровня энергии. Когда Z растёт, наш подход должен дать лучшие результаты, поскольку электрон-электронное отталкивание станет меньше.

До сих пор использовалось очень грубое приближение независимых частиц, в котором электрон-электронное отталкивание полностью исключалось. Разбиение Гамильтониана показанное ниже улучшит результат:

${\displaystyle H={\bar {H_{0}}}+{\bar {H'}}}$

где

${\displaystyle {\bar {H_{0}}}=-{\frac {1}{2}}\nabla _{r_{1}}^{2}+V(r_{1})-{\frac {1}{2}}\nabla _{r_{2}}^{2}+V(r_{2})}$

и

${\displaystyle V(r)=-{\frac {Z-S}{r}}=-{\frac {Z_{e}}{r}}}$

V(r) — центральный потенциал, который выбирается таким образом, что эффект возмущения ${\displaystyle {\bar {H'}}}$ мал. Главный эффект каждого электрона на движение другого заключается в частичной экранировке заряда ядра, так что для V(r) можно взять

${\displaystyle V(r)=-{\frac {Z-S}{r}}=-{\frac {Z_{e}}{r}}}$

где S-постоянная экранирования и Z_e — эффективный заряд. Потенциал соответствует кулоновскому взаимодействию, поэтому индивидуальные энергии электронов (в а. е.) записываются в виде

${\displaystyle E_{0}=-(Z-S)^{2}=-Z_{e}^{2}}$

а соответствующая волновая функция дается

${\displaystyle \psi _{0}(r_{1}\,r_{2})={\frac {Z_{e}^{3}}{\pi }}e^{-Z_{e}(r_{1}+r_{2})}}$

Если Z_е приравнять к 1.70, что увеличить энергию основного состояния, то получится значение, которое согласуются с экспериментальными значение Е₀ = −2.903 а.е энергии основного состояния атома гелия. Поскольку Z = 2, то в этом случае постоянная экранирования S = 0.30. Для основного состояния атома гелия, в приближении средней экранировки, экранирующий эффект каждого электрона на движение другого эквивалентно 1/3 электронного заряда.[4]

Для большей точности в вычислении энергии удобен вариационный принцип для учёта электрон-электронного взаимодействия V_ee  при использовании волновой функции

${\displaystyle \psi _{0}({\vec {r}}_{1},\,{\vec {r}}_{2})={\frac {8}{\pi a^{3}}}e^{-2(r_{1}+r_{2})/a}}$:

${\displaystyle \langle H\rangle =8E_{1}+\langle V_{ee}\rangle =8E_{1}+{\Bigg (}{\frac {e^{2}}{4\pi \epsilon _{0}}}{\Bigg )}{\Bigg (}{\frac {8}{\pi a^{3}}}{\Bigg )}^{2}\int {\frac {e^{-4(r_{1}+r_{2})/a}}{|{\vec {r_{1}}}-{\vec {r_{2}}}|}}\,d^{3}{\vec {r}}_{1}\,d^{3}{\vec {r}}_{2}}$

После интегрирования получим:

${\displaystyle \langle H\rangle =8E_{1}+{\frac {5}{4a}}{\Bigg (}{\frac {e^{2}}{4\pi \epsilon _{0}}}{\Bigg )}=8E_{1}-{\frac {5}{2}}E_{1}=-109+34=-75{\text{ eV}}}$

Это значение ближе к экспериментальному значению, но если использовать лучшую пробную функцию то приближение можно улучшить. Идеальная пробная функция будет учитывать влияние второго электрона. Другими словами, каждый электрон представляет собой облако отрицательного заряда, которое частично экранирует заряд ядра и, таким образом, электрон движется в эффективном потенциале с зарядом ядра Z, который меньше двух. Принимая во внимание это наблюдение волновая функция запишется в виде:

${\displaystyle \psi ({\vec {r}}_{1},{\vec {r}}_{2})={\frac {Z^{3}}{\pi a^{3}}}e^{-Z(r_{1}+r_{2})/a}}$

Используя Z как вариационный параметр для минимизации H. Гамильтониан для этой функции задаётся в виде:

${\displaystyle \langle H\rangle =2Z^{2}E_{1}+2(Z-2){\Bigg (}{\frac {e^{2}}{4\pi \epsilon _{0}}}{\Bigg )}\langle {\frac {1}{r}}\rangle +\langle V_{ee}\rangle }$

Вычисляя средние от ${\displaystyle {\frac {1}{r}}}$ и V_ee гамильтониан приводится к виду:

${\displaystyle \langle H\rangle =[-2Z^{2}+{\frac {27}{4}}Z]E_{1}}$

Минимизируя среднюю энергию по Z находим:

${\displaystyle {\frac {d}{dZ}}{\Bigg (}[-2Z^{2}+{\frac {27}{4}}Z]E_{1}{\Bigg )}=0}$

${\displaystyle Z={\frac {27}{16}}\sim 1.69}$

Это показывает, что второй электрон частично экранирует заряд ядра уменьшая его с 2 до 1,69. В этом случае результат более точный 

${\displaystyle {\frac {1}{2}}{\Bigg (}{\frac {3}{2}}{\Bigg )}^{6}E_{1}=-77.5{\text{ eV}}}$

Где, E₁ представляет ионизационную энергию для атома водорода.

Можно использовать следующую формула для лучшего согласия с экспериментом

${\displaystyle -{\frac {49}{17}}\cdot (1+\alpha )=-2.903386486{\text{ a.u.}}=-79.005153{\text{ eV}}}$

где ${\displaystyle \alpha }$ — постоянная тонкой структуры.

Используя более сложные и точные вариационные функции, основное состояние атома гелия вычислимо с большей точностью и приближается к экспериментальному значению −78.95 eV.[5] Вариационный подход использовался для вычислений этой системы с высокой точносью в работах G.W.F. Drake[6][7][8] и J.D. Morgan III, Jonathan Baker and Robert Hill[9][10][11] используя юазисные функции предложенные Hylleraas или Frankowski-Pekeris. следует заметить что для повышения точности до спектроскопических данных нужно принять во внимание эффекты релятивизма и квантовой электродинамики.[12][13]

Первая энергия ионизации гелия: −24.587387936(25) эВ.[14] Это значение было получено экспериментально.[15] теоретическое значение вторичной ионизации для гелия: −54.41776311(2) эВ. Полная энергия основного состояния атома гелия: −79.005151042(40) эВ или −2.90338583(13) а. е.