Алгоритм Берлекэмпа

Американский математик, профессор Калифорнийского университета Берлекэмп занимался изучением циклических кодов обнаружения и исправления ошибок, в том числе кода Боуза — Чоудхури — Хоквингема, свойства которых зависят от делителей порождающих многочленов. Технические достижения Берлекэмпа в области декодирования этих кодов сделали их более привлекательными с практической точки зрения[1].

Алгоритм был впервые изложен в статье «Factoring Polynomials Over Finite Fields»[2] и позже воспроизведён в книге «Algebraic Coding Theory»[2]. В этой работе 1967 года [3] Берлекэмп пишет, что проблема факторизации возникает в трудах[4] Голомба. Однако, возможность использования матрицы ${\displaystyle B}$ для определения числа нормированных сомножителей многочлена ${\displaystyle f(x)}$ была впервые замечена в статье Карела Петра[5]. В статье Батлера[6] было установлено, что ранг матрицы ${\displaystyle B-E}$ равен ${\displaystyle n-k}$, другое доказательство этого факта было дано Шварцем[7].

Алгоритм Берлекэмпа упоминался во множестве работ[8] и являлся основным алгоритмом решения проблемы факторизации до появления в 1981 году алгоритма Кантора — Цассенхауза[9]. Была разработана техника[10] позволяющая разложить многочлен на множители за ${\displaystyle O(n^{(\omega +1)/2+o(1)}+n^{1+o(1)}\log q),}$ где ${\displaystyle \omega }$ — показатель в оценке сложности перемножения квадратных матриц[11].

Рассматривается задача факторизации многочлена ${\displaystyle f(x)}$ степени ${\displaystyle n}$ (${\displaystyle n\geq 2}$) над конечным полем ${\displaystyle \mathbb {F} _{q}}$ (${\displaystyle q=p^{m}}$, ${\displaystyle p}$ — простое число)[12] на различные неприводимые унитарные многочлены ${\displaystyle f(x)=f_{1}(x)^{e_{1}}\cdots f_{k}(x)^{e_{k}}}$.

Для использования в алгоритме строится матрица ${\displaystyle B=(b_{ij})_{i=0,\;j=0}^{n-1,\;n-1}}$ согласно следующим условиям:

${\displaystyle {x^{iq}}\equiv \sum _{j=0}^{n-1}b_{ij}x^{j}{\pmod {f(x)}}\quad i={\overline {0,n-1}}}$.

Многочлен ${\displaystyle h(x)\in \mathbb {F} _{q}[x]}$ такой, что ${\displaystyle 1\leqslant \deg {h(x)}<n,\quad {h(x)}^{q}\equiv h(x){\pmod {f(x)}}}$, называется ${\displaystyle f}$-разлагающим многочленом[13].

Блок-схема для алгоритма Берлекэмпа — основной случай

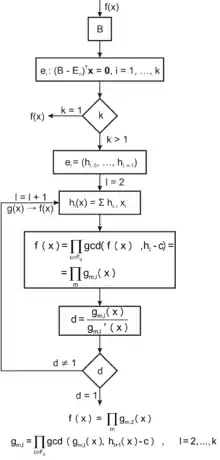
Алгоритм факторизации над конечным полем ${\displaystyle \mathbb {F} _{q}}$ многочлена вида:

${\displaystyle f(x)=f_{1}(x)\cdots f_{k}(x)}$

состоит из следующих шагов:

1. Вычисление матрицы ${\displaystyle B}$[14].
2. Поиск базиса ${\displaystyle {\overline {e_{1}}},\dots ,{\overline {e_{k}}}}$ подпространства решений системы линейных уравнений[15]:

   ${\displaystyle (B-E_{n})^{T}\mathbf {x} =\mathbf {0} }$,

   при этом удаётся выбрать вектор ${\displaystyle {\overline {e_{1}}}=(1,\;0,\;....\;,\;0)}$, так как он всегда будет присутствовать[15] в базисе пространства решений ввиду того, что ${\displaystyle x^{iq}\equiv 1{\pmod {f(x)}}}$ при ${\displaystyle i=0}$.

3. Найденное число ${\displaystyle k}$ есть число неприводимых делителей[14] ${\displaystyle f(x)}$.
   • Если ${\displaystyle k=1}$, то многочлен является неприводимым.
   • Если ${\displaystyle k>1}$, то векторы ${\displaystyle {\overline {e_{l}}}}$ имеют вид ${\displaystyle (h_{l,\;0},\dots ,h_{l,\;n-1})}$. По этим числам строятся ${\displaystyle f}$-разлагающие многочлены:

     ${\displaystyle h_{l}(x)=\sum _{i=0}^{n-1}h_{l,\;i}\;x^{i},\quad l={\overline {2,\;k}},\quad h_{1}(x)=1.}$.

4. Поиск разложения[15]:

   ${\displaystyle f(x)=\prod _{c\in \mathbb {F} _{q},}\gcd(f(x),h_{2}(x)-c)}$

   в виде:

   ${\displaystyle f(x)=\prod _{m}g_{m,\;2}(x)}$,

   где ${\displaystyle g_{m,\;s}(x),\quad s={\overline {2,k}}}$ в общем случае не являются неприводимыми. Функции ${\displaystyle g_{m,\;s}(x)}$ факторизуются таким же способом[15], то есть:

   ${\displaystyle g_{m,\;s}(x)=\prod _{c\in \mathbb {F} _{q},}\gcd(g_{m,\;s}(x),h_{s+1}(x)-c),\quad s={\overline {2,k-1}}}$.

Блок-схема для алгоритма Берлекэмпа — сведение к основному случаю

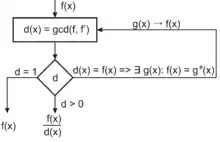
Задача факторизации произвольного унитарного многочлена сводится к рассмотрению основного случая. Для этого вычисляется многочлен

${\displaystyle d(x)=\gcd(f(x),\;f^{'}(x))}$

с применением алгоритма Евклида.

• Если ${\displaystyle d(x)=1,}$ то многочлен не содержит кратных корней, так как кратный корень одновременно является и корнем производной[16].
• Если ${\displaystyle d(x)=f(x),}$ то ${\displaystyle f^{'}(x)=0,}$ и значит ${\displaystyle f(x)=g(x)^{p},\quad g(x)\in \mathbb {F} _{q}[x].}$ Если ${\displaystyle g^{'}(x)=0,}$ то для ${\displaystyle g(x)}$ необходимо проделать описанную процедуру до тех пор пока не будет получено разложение ${\displaystyle f(x)=h(x)^{p^{s}},h{'}(x)\neq 0.}$ Многочлен ${\displaystyle h(x)}$ удовлетворяет требованиям основного случая[16].
• Иначе, многочлен ${\displaystyle d(x)}$ является нетривиальным делителем многочлена ${\displaystyle f(x)}$. В свою очередь, многочлен ${\displaystyle {\frac {f(x)}{d(x)}}}$ не имеет кратных неприводимых сомножителей[16]. Если ${\displaystyle d(x)}$ содержит кратные сомножители, то к нему также применяется описанная процедура. Зная эти разложения, легко получить разложение ${\displaystyle f(x)}$.

Таким образом, задача разложения произвольного унитарного многочлена над конечным полем ${\displaystyle \mathbb {F} _{q}[x]}$ сводится к разложению на множители конечного числа многочленов, которые не имеют кратных неприводимых сомножителей, то есть к основному случаю[16].

Пусть:

${\displaystyle f(x)=f_{1}(x)^{e_{1}}\cdots f_{k}(x)^{e_{k}}}$, где ${\displaystyle \quad e_{i}=1,\quad i={\overline {1,k}}}$.

Согласно китайской теореме об остатках существует единственный многочлен для любого набора ${\displaystyle (c_{1},\;...,\;c_{k})}$ элементов поля ${\displaystyle \mathbb {F} _{q}}$[17]:

${\displaystyle h(x)\in \mathbb {F} _{q}[x],}$

такой что:

${\displaystyle h(x)\equiv c_{i}{\pmod {f_{i}(x)}},\;i={\overline {1,\;k}},\quad \deg {h(x)}<\deg {f(x)}}$.

Многочлен ${\displaystyle h(x)}$ удовлетворяет условию[17]:

${\displaystyle {h(x)}\equiv c_{i}\equiv c_{i}^{q}\equiv h(x)^{q}{\pmod {f_{i}(x)}},\quad i={\overline {1,\;k}}}$,

и поэтому[18]:

${\displaystyle h(x)^{q}\equiv h(x){\pmod {f(x)}},\quad \deg {h(x)}<deg{f(x)}}$.

Из условия:

${\displaystyle h(x)^{q}-h(x)=\prod _{c\in \mathbb {F} _{q}}(h(x)-c)\equiv 0{\pmod {f(x)}}}$,

и из взаимной простоты сомножителей в правой части следует, что каждый неприводимый делитель многочлена ${\displaystyle f(x)}$ делит один, и только один из многочленов ${\displaystyle h(x)-c}$. Таким образом, доказана справедливость и единственность разложения[18]:

${\displaystyle f(x)=\prod _{c\in \mathbb {F} _{q}}\gcd(f(x),h(x)-c).}$

Для нахождения многочлена:

${\displaystyle h(x)=a_{0}+a_{1}x^{1}+\dots +a_{n-1}x^{n-1}\in \mathbb {F} _{q}}$

рассмотрим сравнение:

${\displaystyle h(x)^{q}\equiv h(x){\pmod {f(x)}}}$,

которое равносильно условию[17]:

${\displaystyle \sum _{i=0}^{n-1}a_{i}x^{iq}\equiv \sum _{i=0}^{n-1}a_{i}x^{i}{\pmod {f(x)}}}$.

По определению матрицы ${\displaystyle B}$ получим:

${\displaystyle \sum _{i=0}^{n-1}a_{i}\sum _{j=0}^{n-1}b_{ij}x^{j}=\sum _{i=0}^{n-1}a_{i}x^{i}}$,

поэтому[17]:

${\displaystyle \sum _{i=0}^{n-1}a_{i}b_{ij}=a_{j},\quad j={\overline {0,\;n-1}}}$.

Полученная система уравнений определяет коэффициенты ${\displaystyle f}$-разлагающих многочленов и может быть записана в виде:

${\displaystyle \quad (a_{0},\;a_{1},...,a_{n-1})B=(a_{0},\;a_{1},\;...,a_{n-1})}$

или:

${\displaystyle \quad (a_{0},\;a_{1},...,a_{n-1})(B-E_{n})=\mathbf {0} }$[17].

Сложность алгоритма составляет ${\displaystyle O(n^{3}+qkn)}$ математических операций[19]. Алгоритм будет эффективен только для небольших полей. Это связанно с необходимостью перебора всех ${\displaystyle c\in \mathbb {F} _{q}}$.

• В случае простого поля, если значение ${\displaystyle p}$ велико, то перебор значений ${\displaystyle c\in {\mathbb {Z} /p\mathbb {Z} }}$ займёт много времени. Однако, возможно определить множество ${\displaystyle M}$, состоящее из ${\displaystyle c}$, для которых ${\displaystyle \gcd(f(x),h(x)-c)}$ нетривиален[20]. Для этого необходимо найти корни результанта[21] ${\displaystyle R(c)}$, которые и будут составлять множество ${\displaystyle M}$.
• Ещё один метод разложения унитарного многочлена ${\displaystyle f(x)\in GF(q)[x]}$, не имеющего кратных неприводимых множителей, основан на приведении некоторой эффективно вычислимой с помощью алгоритма Берлекэмпа матрицы A к диагональному виду[22]. Однако сам процесс диагонализации довольно сложен.
• В работе Калтофена и Лобо[23] была предложена вероятностная версия алгоритма Берлекэмпа, позволяющая разложить на множители многочлен ${\displaystyle f(x)\in GF(q)[x]}$ степени ${\displaystyle n}$ за ${\displaystyle O((n\log n+\log q)\cdot n(\log n)\log(\log n))}$ арифметических операций. Алгоритм Калтофена — Лобо был реализован на компьютере, и оказался эффективным для многочленов высокой степени, например, для многочленов степени 10001 над полем ${\displaystyle \mathbb {Z} /127\mathbb {Z} }$ он работает около 102,5 часов на компьютере Sun-4.

Алгоритмы факторизации многочленов важны для теории кодирования и для изучения линейных рекуррентных соотношений в конечных полях. Также алгоритм Берлекэмпа используется для вычисления группы Галуа уравнения над полем рациональных чисел и построения решений полей, разложения многочленов над кольцом целых чисел, для отыскания разложения простого рационального числа в поле алгебраических чисел, и для некоторых других вычислительных задач[24]. Алгоритмы с факторными базами используют алгоритмы факторизации многочленов для решения задачи отыскания дискретного логарифма[25], на вычислительной сложности которой, построена схема Эль-Гамаля.

В системе компьютерной алгебры PARI/GP алгоритм Берлекэмпа может быть использован посредством команды factormod[26].

• Berlekamp, Elwyn R. Factoring Polynomials Over Finite Fields (англ.) // Bell System Technical Journal. — 1967. — Vol. 46. — P. 1853—1859. BSTJ Later republished in: Berlekamp, Elwyn R. Algebraic Coding Theory (англ.). — McGraw-Hill Education, 1968. — ISBN 0-89412-063-8.
• Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М.: МЦНМО, 2003. — 328 с. — ISBN 5-94057-103-4.
• Лидл Р., Нидеррайтер Г. Конечные поля = Finite Fields / Под ред. В. И. Нечаева. — 1-е изд. — М.: Мир, 1988. — Т. 1. — 430 с. — ISBN 5-03-000065-8.
• Ван дер Варден Б.Л. Алгебра. — M.: Наука, 1976. — 646 с. Архивная копия от 2 ноября 2013 на Wayback Machine