Адаптивный алгоритм Хаффмана

Он позволяет динамически регулировать дерево Хаффмана, не имея начальных частот. В ФГК дереве Хаффмана есть особый внешний узел, называемый 0-узел, используемый для идентификации входящих символов. То есть, всякий раз, когда встречается новый символ — его путь в дереве начинается с нулевого узла. Самое важное — то, что нужно усекать и балансировать ФГК дерево Хаффмана при необходимости, и обновлять частоту связанных узлов. Как только частота символа увеличивается, частота всех его родителей должна быть тоже увеличена. Это достигается путём последовательной перестановки узлов, поддеревьев или и тех и других.

Важной особенностью ФГК дерева является принцип братства (или соперничества): каждый узел имеет два потомка (узлы без потомков называются листами) и веса идут в порядке убывания. Благодаря этому свойству дерево можно хранить в обычном массиве, что увеличивает производительность.[1][2]

Код представляется в виде древовидной структуры, в которой каждый узел имеет соответствующий вес и уникальный номер.

Цифры идут вниз, и справа налево.

Веса должны удовлетворять принципу братства. Таким образом, если А является родительским узлом B и C является потомком B, то ${\displaystyle W(A)>W(B)>W(C)}$.

Вес — это всего лишь количество символов, встреченных ранее.

Набор узлов с одинаковыми весами представляют собой блок.

Чтобы получить код для каждого узла, в случае двоичного дерева мы могли бы просто пройти все пути от корня к узлу, записывая, например, «1» если мы идем направо, и «0» если мы пойдем налево.

Также в этом алгоритме используется специальный лист (узел без потомков), NYT (от англ. not yet transmitted — ещё не переданный символ), из которого «растут» новые, ранее не встречавшиеся, символы.

Кодер и декодер начинают только с корневого узла, который имеет максимальный вес. В начале это и есть наш NYT узел.

Когда мы передаем NYT символ, мы должны передать вначале код самого узла, а затем данные.

Для каждого символа, который уже находится в дереве, мы должны только передавать код конечных узлов (листов).

Для каждого передающегося символа передатчик и приёмник выполняют процедуру обновления:

1. Если текущий символ является не встречавшимся — добавить к NYT два дочерних узла: один для следующего NYT, другой для символа. Увеличить вес нового листа и старого NYT и переходить к шагу 4. Если текущий символ является не NYT, перейти к листу символа.
2. Если этот узел не имеет наибольший вес в блоке, поменять его с узлом, имеющим наибольшее число, за исключением, если этот узел является родительским элементом[3]
3. Увеличение веса для текущего узла
4. Если это не корневой узел зайти в родительский узел затем перейдите к шагу 2. Если это корень, окончание.

Примечание: замена узлов означает замену весов и соответствующих символов, но не чисел.

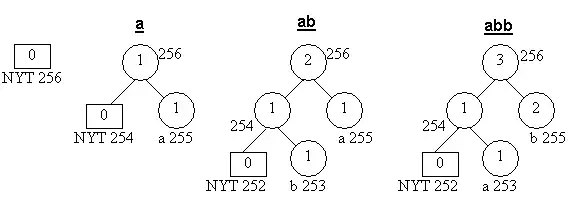
Начинаем с пустого дерева.

Для «a» передаём его двоичный код.

NYT порождает два дочерних узла: 254 и 255. Увеличиваем вес корня. Код «a», связанный с узлом 255, становится 1.

Для «b» передавать 0 (код NYT узла), затем его двоичный код.

NYT порождает два дочерних узла: 252 для NYT и 253 для b. Увеличиваем веса 253, 254 и корня. Код для «b» равен 01.

Для следующего «b» передаётся 01.

Идём в лист 253. У нас есть блок весов в 1 и наибольшее число в блоке 255, так что меняем веса и символы узлов 253 и 255, увеличиваем вес, идём в корень и увеличиваем вес корня.

В будущем код «b» — это 1, а для «a» — это теперь 01, который отражает их частоту.