(1235) Шоррия
(1235) Шоррия (лат. Schorria) — астероид, относящийся к группе астероидов пересекающих орбиту Марса, который характеризуется одним из самых длительных периодов вращения среди всех известных астероидов — порядка 52 суток и 17 часов. Он был обнаружен 18 октября 1931 года немецким астрономом Карлом Рейнмутом в обсерватории Хайдельберг в Германии и назван в честь немецкого астронома Рихарда Шорра[2].
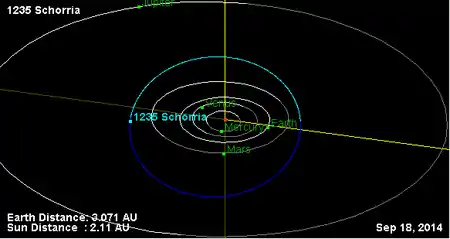
Орбита астероида Шоррия и его положение в Солнечной системе
| (1235) Шоррия | |
|---|---|
| Астероид | |
| Открытие | |
| Первооткрыватель | Карл Рейнмут |
| Место обнаружения | Хайдельберг |
| Дата обнаружения | 18 октября 1931 |
| Альтернативные обозначения | 1931 UJ; 1988 HD |
| Категория |
Марс-кроссеры (Семейство Венгрии) |
| Орбитальные характеристики | |
|
Эпоха 23 мая 2014 года JD 2456800.5 |
|
| Эксцентриситет (e) | 0,1545912 |
| Большая полуось (a) |
285,762 млн км (1,9101993 а. е.) |
| Перигелий (q) |
241,585 млн км (1,6148993 а. е.) |
| Афелий (Q) |
329,938 млн км (2,2054993 а. е.) |
| Период обращения (P) | 964,31 сут (2,64 г.) |
| Средняя орбитальная скорость | 21,421 км/с |
| Наклонение (i) | 25,00221° |
| Долгота восходящего узла (Ω) | 12,96852° |
| Аргумент перигелия (ω) | 43,72315° |
| Средняя аномалия (M) | 81,87504° |
| Физические характеристики[1] | |
| Диаметр | 9 км |
| Период вращения | 1265 ч |
| Спектральный класс | K |
| Видимая звёздная величина | 15,35m (текущая) |
| Абсолютная звёздная величина | 12,68m |
| Альбедо | 0,06 |
| Текущее расстояние от Солнца | 1,808 а. е. |
| Текущее расстояние от Земли | 1,072 а. е. |
Фотометрические наблюдения, проведённые с февраля по апрель 2009 года, позволили получить кривые блеска этого тела, из которых следовало, что период вращения астероида вокруг своей оси равняется 1265 ± 80 часам, с изменением блеска по мере вращения 0,43 ± 0,02 m[1].
См. также
Примечания
- Warner, Brian D.; Stephens, Robert D. The Lightcurve for the Long-Period Hungaria Asteroid 1235 Schorria (англ.) // The Minor Planet Bulletin (ISSN 1052-8091) : journal. — 2009. — Vol. 36, no. 3. — P. 102—103. — .
- Schmadel, Lutz D. Dictionary of Minor Planet Names (англ.). — Fifth Revised and Enlarged Edition. — B., Heidelberg, N. Y.: Springer, 2003. — P. 103. — ISBN 3-540-00238-3.
Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.