Эпюр

Эпю́р (фр. epure — чертёж) — чертёж, на котором пространственная фигура изображена методом нескольких (по ГОСТу трёх, но не всегда) плоскостей. Обычно оно даёт 3 вида: фронтальную, горизонтальную и профильную проекции (фасад, план, профиль). Чертёж проецируется на взаимно перпендикулярные, а затем развернутые на одну плоскости.

Самолёт Hawker Sea Hawk, изображённый с помощью эпюра Монжа

История

Чертёж двухдечного линейного корабля HMS Jersey, 1733

Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, то есть возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путём простых приемов определить размеры отрезков линий и фигур.

В первой половине XVIII века в европейском кораблестроении сложилась практика располагать проекцию теоретического чертёжа (совмещённую с видом ютовых надстроек с кормы), которая примерно соответствовала современной проекции «Корпус», слева от основного вида с правого борта, ныне называемого «Бок», а проекцию «Полуширота» — под последним.

Будучи одним из министров в революционном правительстве Франции, Гаспар Монж много сделал для её защиты от иностранной интервенции и для победы революционных войск. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке — начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года[1] (стенографическая запись лекций была сделана в 1795 году).

Система двух плоскостей проекции

рис.1 Система двух плоскостей проекций: а — расположение плоскостей проекций; б — совмещение плоскостей проекций

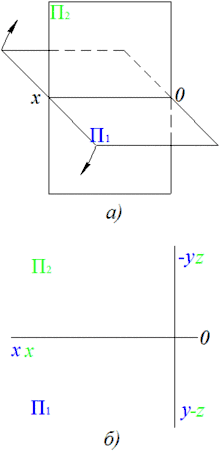
В данном случае, для построения изображения в двух плоскостях проекций, горизонтальная плоскость проекций П₁ и фронтальная плоскость проекций П₂ совмещаются в одну, как показано на рис.1. В пересечении они дают ось проекций x и делят пространство на четыре четверти (квадранта).

Система трех плоскостей проекций

рис.2 Система трех плоскостей проекций: а — расположение плоскостей проекций; б — совмещение плоскостей проекций

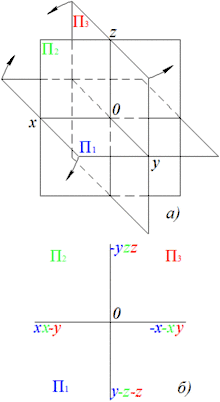
В системе трех плоскостей проекций совмещаются все три плоскости проекций (П₁ — горизонтальная, П₂ — фронтальная и П₃ — профильная), как показано на рис.2. Плоскости образуют три оси проекций (оси координат) и восемь прямоугольных трехгранников, деля пространство на восемь октантов. Для проецирования точки А на плоскости проекций используются следующие её координаты: П₁ — А′(x, y) П₂ — А′′(x, z) П₃ — А′′′(y, z)

См. также

Эпюра

Примечания

Monge G. Géométrie descriptive. — Paris, 1799. — 132 p.

Литература

Краткий справочник по начертательной геометрии и машиностроительному черчению / Н. П. Сберегаев, М. А. Герб. М. — Л., Машиностроение, 1965, 264с.
Курс начертательной геометрии / В. О. Гордон, М. А. Семенцов-Огиевский. М.: Наука. 1971. 367с.
Краткий курс начертательной геометрии / И. С. Альтшулер. Минск, Высшая школа, 1965. 271с.
Начертательная геометрия / С. А. Фролов. — М.: Машиностроение, 1978 — 240с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Monge G. Géométrie descriptive. — Paris, 1799. — 132 p.