Эллиптический фильтр

АЧХ эллиптического фильтра низких частот четвёртого порядка с ε=0,5 и ξ=1,05. Также показано минимальное усиление в полосе пропускания, максимальное усиление в полосе подавления и переходная зона между частотами (нормированными) 1 и ξ

Переходная зона (увеличено).

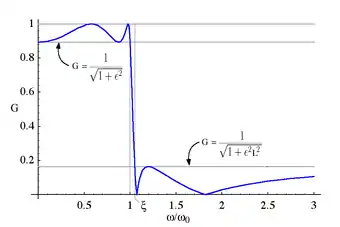
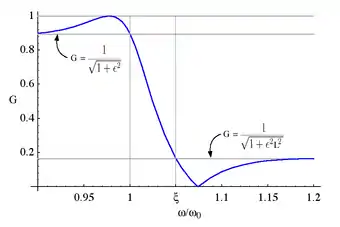
• В полосе пропускания эллиптическая функция меняет значения от нуля до единицы. АЧХ в полосе пропускания, таким образом, варьирует от единицы до ${\displaystyle 1/{\sqrt {1+\epsilon ^{2}}}}$.

• В полосе подавления эллиптическая функция меняет значения от бесконечности до значения ${\displaystyle L_{n}}$, которое определяется как:

${\displaystyle L_{n}=R_{n}(\xi ,\xi )}$

АЧХ в полосе подавления, таким образом, меняет значения от нуля до ${\displaystyle 1/{\sqrt {1+\epsilon ^{2}L_{n}^{2}}}}$.

• Предельный случай ${\displaystyle \xi \rightarrow \infty }$ превращает эллиптическую функцию в многочлен Чебышёва, и, таким образом, эллиптический фильтр становится фильтром Чебышёва I рода с показателем пульсаций ε.
• Так как фильтр Баттерворта является предельным случаем фильтра Чебышёва, то при выполнении условий ${\displaystyle \xi \rightarrow \infty }$, ${\displaystyle \omega _{0}\rightarrow 0}$ и ${\displaystyle \epsilon \rightarrow 0}$ так что ${\displaystyle \epsilon \,R_{n}(\xi ,1/\omega _{0})=1}$ эллиптический фильтр становится фильтром Баттерворта.
• Предельный случай ${\displaystyle \xi \rightarrow \infty }$, ${\displaystyle \epsilon \rightarrow 0}$ и ${\displaystyle \omega _{0}\rightarrow 0}$ так что ${\displaystyle \xi \omega _{0}=1}$ и ${\displaystyle \epsilon L_{n}=\alpha }$ превращает эллиптический фильтр в фильтр Чебышёва II рода с АЧХ

${\displaystyle G(\omega )={\frac {1}{\sqrt {1+{\frac {1}{\alpha ^{2}T_{n}^{2}(1/\omega )}}}}}.}$

Логарифм модуля АЧХ эллиптического фильтра 8 порядка на плоскости комплексной частоты (s=σ+jω) с ε=0,5, ξ=1,05 и ${\displaystyle \omega _{0}=1}$. Белые пятна — полюса, тёмные — нули. Всего на графике 16 полюсов и 8 нулей второго порядка. На графике чёрный цвет соответствует усилению менее 0,0001, а белый — усилению более 10.

Переходная зона фильтра (увеличено).

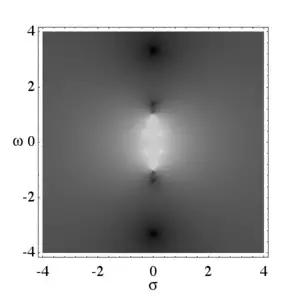
Нули модуля АЧХ совпадают с полюсами дробно-рациональной эллиптической функции.

Полюса эллиптического фильтра могут быть определены так же, как и полюса фильтра Чебышёва I рода. Для простоты примем частоту среза равной единице. Полюса ${\displaystyle (\omega _{pm})}$ эллиптического фильтра будут нулями знаменателя амплитудной характеристики. Используя комплексную частоту ${\displaystyle s=\sigma +j\omega ,}$ получим:

${\displaystyle 1+\epsilon ^{2}R_{n}^{2}(-js,\xi )=0}$

Пусть ${\displaystyle -js=\mathrm {cd} (w,1/\xi )}$, где cd — эллиптическая косинус-функция Якоби. Тогда, используя определение эллиптической дробно-рациональной функции, получим:

${\displaystyle 1+\epsilon ^{2}\mathrm {cd} ^{2}\left({\frac {nwK_{n}}{K}},{\frac {1}{L_{n}}}\right)=0}$

где ${\displaystyle K=K(1/\xi )}$ and ${\displaystyle K_{n}=K(1/L_{n})}$. Разрешив относительно w

${\displaystyle w={\frac {K}{nK_{n}}}\mathrm {cd} ^{-1}\left({\frac {\pm j}{\epsilon }},{\frac {1}{L_{n}}}\right)+{\frac {mK}{n}},}$

где значения обратной cd-функции сделаны явными при помощи целого индекса m.

Полюса эллиптической функции в таком случае:

${\displaystyle s_{pm}=i\,\mathrm {cd} (w,1/\xi ).}$

Как и в случае многочленов Чебышёва, это можно выразить в явной комплексной форме [1]

${\displaystyle s_{pm}={\frac {a+jb}{c}},}$

${\displaystyle a=-\zeta _{n}{\sqrt {1-\zeta _{n}^{2}}}{\sqrt {1-x_{m}^{2}}}{\sqrt {1-x_{m}^{2}/\xi ^{2}}},}$

${\displaystyle b=x_{m}{\sqrt {1-\zeta _{n}^{2}(1-1/\xi ^{2})}},}$

${\displaystyle c=1-\zeta _{n}^{2}+x_{i}^{2}\zeta _{n}^{2}/\xi ^{2},}$

где ${\displaystyle \zeta _{n}}$ — функция от ${\displaystyle n,\,\epsilon }$, а ${\displaystyle \xi }$ и ${\displaystyle x_{m}}$ — нули эллиптической функции. Функция ${\displaystyle \zeta _{n}}$ определена для всех n в смысле эллиптической функции Якоби. Для порядков 1 и 2 имеем

${\displaystyle \zeta _{1}={\frac {1}{\sqrt {1+\epsilon ^{2}}}},}$

${\displaystyle \zeta _{2}={\frac {2}{(1+t){\sqrt {1+\epsilon ^{2}}}+{\sqrt {(1-t)^{2}+\epsilon ^{2}(1+t)^{2}}}}},}$

где

${\displaystyle t={\frac {1}{\sqrt {1-1/\xi ^{2}}}}.}$

Рекурсивные свойства эллиптических функций можно использовать для построения выражений более высокого порядка для ${\displaystyle \zeta _{n}}$:

${\displaystyle \zeta _{m\cdot n}(\xi ,\epsilon )=\zeta _{m}\left(\xi ,{\sqrt {{\frac {1}{\zeta _{n}^{2}(L_{m},\epsilon )}}-1}}\right),}$

где ${\displaystyle L_{m}=R_{m}(\xi ,\xi ).}$

Нормированные добротности для полюсов эллиптического фильтра восьмого порядка с ξ=1,1 как функции показателя пульсаций ε. Каждая кривая представляет четыре полюса, так как комплексно сопряжённые и противоположные по знаку пары полюсов имеют одинаковую добротность. Добротность всех полюсов имеет минимум при ε_Qmin=1/√L_n=0,02323…

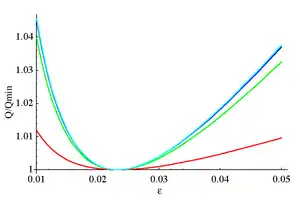
См.[2] Эллиптические фильтры обычно определяются путём задания определённой величины пульсаций в полосе пропускания, полосе подавления и крутизной амплитудной характеристики. Эти характеристики являются определяющими для задания минимального порядка фильтра. Другой подход к проектирования эллиптического фильтра заключается в определении чувствительности амплитудной характеристики аналогового фильтра к значениям его электронных компонент. Эта чувствительность обратно пропорциональна специальному показателю (добротности) полюсов передаточной функции фильтра. Добротностью полюса определяется как:

${\displaystyle Q=-{\frac {|s_{pm}|}{2\mathrm {Re} (s_{pm})}}=-{\frac {1}{2\cos(\arg(s_{pm}))}}}$

и является мерой влияния данного полюса на общую амплитудную характеристику. Для эллиптического фильтра заданного порядка существует связь между показателем пульсаций и фактором селективности, который минимизирует добротность всех полюсов передаточной функции:

${\displaystyle \epsilon _{Qmin}={\frac {1}{\sqrt {L_{n}(\xi )}}}}$

Это приводит к существованию фильтра, наименее чувствительного к изменению параметров компонент фильтра, однако при таком способе проектирования теряется возможность независимо назначать величину пульсаций в полосе пропускания и полосе подавления. Для таких фильтров при увеличении порядка пульсации как в полосе подавления, так и в полосе пропускания уменьшаются, а крутизна характеристики вокруг частоты среза увеличивается. При расчёте фильтра с минимальной добротностью необходимо учитывать, что порядок такого фильтра будет больше, чем при обычном методе расчёта. График модуля амплитудной характеристики будет выглядеть практически так же, как и раньше, однако полюса будут располагаться не по эллипсу, а по кругу, причём в отличие от фильтра Баттерворта, полюса которого также располагаются по кругу, расстояние между ними будет неодинаковым, а на мнимой оси будут располагаться нули.

Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:

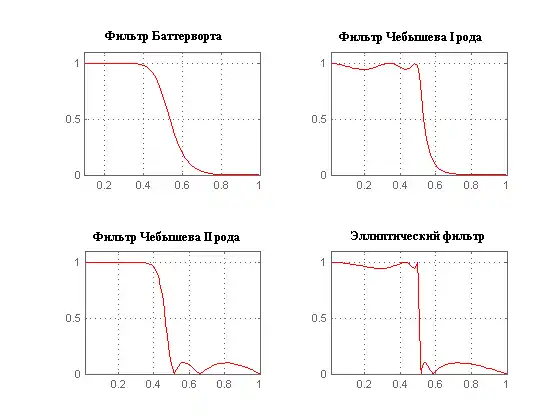
Как следует из графика, эллиптический фильтр имеет наибольшую крутизну характеристики, однако он также обладает и значительными пульсациями как в полосе пропускания, так и в полосе подавления.

• Цифровая обработка сигналов
• Цифровая обработка изображений
• Электронный фильтр
• Решётчатый фильтр
• БИХ-фильтр

• В.А. Лукас. Теория автоматического управления. — M.: Недра, 1990.
• Б.Х. Кривицкий. Справочник по теоретическим основам радиоэлектроники. — М.: Энергия, 1977.
• Miroslav D. Lutovac. Filter Design for Signal Processing using MATLAB© and Mathematica©. — New Jersey, USA.: Prentice Hall, 2001. — ISBN 0-201-36130-2.
• Richard W. Daniels. Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1974. — ISBN 0-07-015308-6.
• Steven W. Smith. The Scientist and Engineer’s Guide to Digital Signal Processing. — Second Edition. — San-Diego: California Technical Publishing, 1999. — ISBN 0-9660176-4-1.
• Britton C. Rorabaugh. Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1999. — ISBN 0-07-054004-7.
• B. Widrow, S.D. Stearns. Adaptive Signal Processing. — Paramus, NJ: Prentice-Hall, 1985. — ISBN 0-13-004029-0.
• S. Haykin. Adaptive Filter Theory. — 4rd Edition. — Paramus, NJ: Prentice-Hall, 2001. — ISBN 0-13-090126-1.
• Michael L. Honig, David G. Messerschmitt. Adaptive Filters — Structures, Algorithms, and Applications. — Hingham, MA: Kluwer Academic Publishers, 1984. — ISBN 0-89838-163-0.
• J.D. Markel, A.H. Gray, Jr. Linear Prediction of Speech. — New York: Springer-Verlag, 1982. — ISBN 0-387-07563-1.
• L. R. Rabiner, R.W. Schafer. Digital Processing of Speech Signals. — Paramus, NJ: Prentice-Hall, 1978. — ISBN 0-13-213603-1.
• Richard J. Higgins. Digital Signal Processing in VLSI. — Paramus, NJ: Prentice-Hall, 1990. — ISBN 0-13-212887-X.
• A. V. Oppenheim, R. W. Schafer. Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1975. — ISBN 0-13-214635-5.
• L. R. Rabiner, B. Gold. Theory and Application of Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1986. — ISBN 0-13-914101-4.
• John G. Proakis, Dimitris G. Manolakis. Introduction to Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1988. — ISBN 0-02-396815-X.

• Расчет эллиптического фильтра с примерами
• Фильтры нижних частот
• Расчёт рекурсивных фильтров
• Сравнение линейных фильтров (англ.)