Экваториальное утолщение
Экваториальное утолщение, экваториальный балдж (англ. Equatorial bulge) — различие между экваториальным и полярным диаметрами планеты, возникающее вследствие центробежной силы, вызванной вращением вокруг оси тела. Вращающееся тело стремится к формированию сжатого сфероида, а не шара.
На Земле
Земля обладает слабо выраженным экваториальным утолщением: на экваторе она примерно на 43 км шире, чем расстояние от полюса до полюса, это различие составляет 1/300 часть диаметра. Если Землю представить в виде глобуса диаметром 1 метр на экваторе, то различие составило бы только 3 миллиметра. Несмотря на то, что визуально такое различие незаметно, но оно вдвое превышает наибольшее отклонение настоящей поверхности от эллипсоида, включая наиболее высокие горы и океанские впадины.
Вращение Земли также влияет на уровень моря, воображаемую поверхность, которая используется как нуль-пункт измерения высот. Такая поверхность совпадает со средним уровнем воды в океанах и может быть обобщена на поверхность Земли, если принять во внимание локальное значение гравитационного потенциала и центробежной силы.
Разность радиусов составляет около 21 км. Наблюдатель, находящийся на уровне моря на географическом полюсе на 21 км ближе к центру Земли, чем наблюдатель на уровне моря на экваторе. В результате наиболее высокая точка на поверхности Земли, если измерять высоту от центра Земли, — пик горы Чимборасо в Эквадоре, а не гора Эверест. Но поскольку океан также поверхность океана также имеет утолщение, как и поверхность Земли, и атмосфера, то относительно уровня моря Чимборасо не столь высока, как Эверест.
Более точно, поверхность Земли обычно приближают сжатым эллипсоидом для того, чтобы можно было точно определить сетку широт и долгот для нужд картографии, а также понятие центра Земли. В стандарте WGS-84 земной эллипсоид, широко используемый для создания карт и осуществления системы GPS, соответствует радиусу Земли на экваторе 6378,137 ± км и на полюсе 6356,7523142 ± км; разница радиусов составляет 21,3846858 ± км, разница диаметров равна 42,7693716 ± км, сплюснутость равна 1/298,257223563. Уровень поверхности моря гораздо ближе к этому стандартному эллипсоиду, чем поверхность твёрдой Земли.
Равновесие как баланс энергий
Гравитация стремится сжать небесное тело и привести его к форме шара, в которой вся масса наиболее близко расположена к центру. Вращение возмущает сферическую форму; обычно мерой такого возмущения считают сплюснутость, которая может зависеть от разных факторов, включая размер, угловую скорость, плотность и эластичность.
Для того, чтобы лучше понять тип равновесия, которое выполняется в данной ситуации, представим человека, сидящего во вращающемся кресле и держащего груз в руках. Если человек притянет груз к себе, он совершит работу и увеличит кинетическую энергию вращения. Скорость вращения возрастает, увеличивается и центробежная сила.
Нечто похожее происходит и при формировании планет. Вещество сначала осаждается в виде медленно вращающегося диска, затем столкновения и трение переводят кинетическую энергию в тепло, что позволяет диску превратиться в очень сплюснутый сфероид.
Пока протопланета слишком сплюснута для того, чтобы оставаться в равновесии, выделение гравитационной потенциальной энергии сжатия увеличивает кинетическую энергию вращения. По мере продолжения сжатия темп вращения усиливается, поэтому необходимая энергия для сжатия возрастает. Существует точка, при которой увеличение кинетической энергии вращения при дальнейшем сжатии будет больше, чем количество выделяемой гравитационной энергии. Процесс сжатия происходит только до момента достижения этой точки.
Поскольку равновесие нарушается, может возникать мощная конвекция, то появляющееся при этом трение может превращать кинетическую энергию в тепло, в итоге уменьшая общую кинетическую энергию системы. При достижении равновесия крупномасштабный переход кинетической энергии в тепловую затухает. В этом смысле состояние равновесия соответствует состоянию минимальной энергии, которое можно достичь.
Скорость вращения Земли постепенно уменьшается на две тысячные секунды за каждые 100 лет.[1] Оценки того, как быстро Земля вращалась в прошлом, очень различаются, поскольку точно не известно, когда сформировалась Луна. Оценки темпа вращения Земли 500 млн лет назад составляют около 20 современных часов в сутки.
Темп вращения Земли замедляется в основном из-за приливного взаимодействия с Луной и Солнцем. Поскольку твёрдые участки Земли деформируются, то экваториальное утолщение уменьшается по мере уменьшения скорости вращения.
Различие в гравитационном ускорении
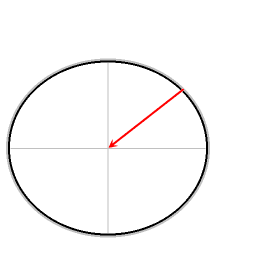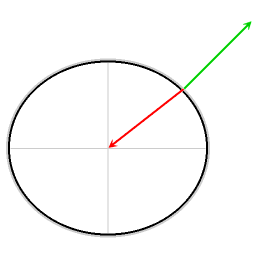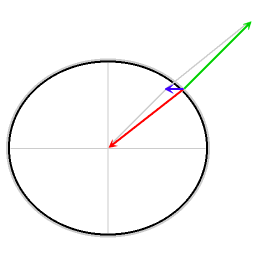
Красная стрелка: гравитация.
Зелёная стрелка: сила реакции опоры.
Синяя стрелка: результирующая сила.
Результирующая сила представляет собой необходимую центростремительную силу. Без такой силы объекты без трения соскользнули бы к экватору.
При вычислениях, когда используется система координат, вращающаяся вместе с Землёй, вектор центробежной силы направлен вовне, он примерно такой же по величине, как вектор центростремительной силы.
Поскольку планета вращается вокруг своей оси, то на экваторе сила тяжести меньше, чем у полюсов. В XVII веке вслед за изобретением маятниковых часов французские учёные обнаружили, что часы, отправленные во Французскую Гвиану, идут медленнее, чем их копии в Париже. Измерения ускорения, возникающего под действием гравитации, на экваторе также учитывают вращение планеты. Любой объект, находящийся неподвижно относительно поверхности Земли, в реальности движется по круговой орбите вокруг оси вращения Земли. Удерживание объекта на круговой орбите требует постоянной силы. Ускорение, которое необходимо для движения вокруг оси вращения Земли вдоль экватора при обороте за сутки, равно 0,0339 м/с². Наличие такого ускорения уменьшает эффективное гравитационное ускорение. На экваторе эффективное гравитационное ускорение равно 9,7805 м/с2. Это означает, что истинное гравитационное ускорение на экваторе должно быть равно 9,8144 м/с2 (9,7805 + 0,0339 = 9,8144).
На полюсах гравитационное ускорение составляет 9,8322 м/с2. Разность 0,0178 м/с2 между гравитационным ускорением на полюсах и истинным гравитационным ускорением на экваторе возникает потому, что на экваторе объекты на 21 км дальше от центра Земли, чем на полюсах.
В целом, два фактора вносят вклад в уменьшение эффективного ускорения на экваторе по сравнению с полюсами. Около 70% различия возникает из-за вращения, около 30% вносит несферичность Земли.
Диаграмма иллюстрирует тот факт, что на всех широтах эффективное гравитационное ускорение уменьшается из-за требуемой центростремительной силы, сильнее всего уменьшение на экваторе.
Влияние на орбиты спутников
Отличие гравитационного поля Земли от сферически симметричного влияет также на форму орбиты спутников вследствие вековой прецессии орбиты.[2][3][4] Форма орбит зависит от ориентации оси вращения Земли в инерциальном пространстве, и, в общем случае, влияет на все кеплеровы элементы орбиты за исключением большой полуоси. Если ось z системы координат направлена вдоль оси симметрии Земли, то вековую прецессию будут испытывать долгота восходящего узла Ω, аргумент перицентра ω и средняя аномалия M.[5]
Такие возмущения, ранее использовавшиеся для получения карты гравитационного поля Земли со спутников,[6] могут играть важную роль и при тестировании выводов общей теории относительности,[7] поскольку гораздо меньшие эффекты теории относительности сложно отличить от проявлений сплюснутости Земли.
Другие небесные тела
Обычно вращающиеся небесные тела (и достаточно массивные для того, чтобы поддерживать шарообразную или близкую к ней форму) обладают экваториальным утолщением, по величине соответствующим скорости вращения. Сатурн среди планет Солнечной системы обладает наибольшим утолщением (11 808 км).
В следующей таблице представлены параметры экваториального утолщения некоторых крупных тел Солнечной системы.
| Объект | Экваториальный диаметр | Полярный диаметр | Экваториальное утолщение | Сплюснутость |
|---|---|---|---|---|
| Земля | 12 756,27 км | 12 713,56 км | 42,77 км | 1:298,2575 |
| Марс | 6805 км | 6754,8 км | 50,2 км | 1:135,56 |
| Церера | 975 км | 909 км | 66 км | 1:14,77 |
| Юпитер | 143 884 км | 133 709 км | 10 175 км | 1:14,14 |
| Сатурн | 120 536 км | 108 728 км | 11 808 км | 1:10,21 |
| Уран | 51 118 км | 49 946 км | 1172 км | 1:43,62 |
| Нептун | 49 528 км | 48 682 км | 846 км | 1:58,54 |
Экваториальные балджи не следует путать с экваториальными хребтами. Экваториальные хребты являются особенностью структуры по крайней мере нескольких спутников Сатурна: Япета, Атласа, Пана и Дафниса. Такие хребты располагаются вдоль экватора спутников. Вероятно, хребты являются свойством исключительно спутников Сатурна, но пока не ясно, так ли это. Хребты на первых трёх спутниках были обнаружены аппаратом Кассини-Гюйгенс в 2005 году, хребет на Дафнисе открыт в 2017 году. Хребет на Япете достигает 20 км в ширину, 13 км в высоту и 1300 км в длину. Хребет на Атласе даже более заметен, если принять во внимание меньший размер спутника, и придаёт Атласу уплощённую форму. Изображения Пана показывают структуру, похожую на хребет на Атласе, а на Дафнисе структура менее выражена.
Формализация
Коэффициент сплюснутости в состоянии равновесия самогравитирующего сфероида, состоящего из несжимаемой жидкости с однородным распределением плотности и вращающегося вокруг фиксированной оси, при малом сжатии выражается в виде[8]
где и являются экватоиальным и полярным радиусами, — средний радиус, — угловая скорость, — период вращения, — универсальная гравитационная постоянная, — полная масса тела, — плотность тела.
Примечания
- Hadhazy, Adam Fact or Fiction: The Days (and Nights) Are Getting Longer. Scientific American. Дата обращения: 5 декабря 2011.
- Iorio, L. Perturbed stellar motions around the rotating black hole in Sgr A* for a generic orientation of its spin axis (англ.) // Physical Review D : journal. — 2011. — Vol. 84, no. 12. — P. 124001. — doi:10.1103/PhysRevD.84.124001. — . — arXiv:1107.2916.
- Renzetti, G. Satellite Orbital Precessions Caused by the Octupolar Mass Moment of a Non-Spherical Body Arbitrarily Oriented in Space (англ.) // Journal of Astrophysics and Astronomy : journal. — 2013. — Vol. 34, no. 4. — P. 341—348. — doi:10.1007/s12036-013-9186-4. — .
- Renzetti, G. Satellite orbital precessions caused by the first odd zonal J3 multipole of a non-spherical body arbitrarily oriented in space (англ.) // Astrophysics and Space Science : journal. — 2014. — Vol. 352, no. 2. — P. 493—496. — doi:10.1007/s10509-014-1915-x. — .
- King-Hele, D. G. The Earth's Gravitational Potential, deduced from the Orbits of Artificial Satellites (англ.) // Geophysical Journal : journal. — 1961. — Vol. 4, no. 1. — P. 3—16. — doi:10.1111/j.1365-246X.1961.tb06801.x. — .
- King-Hele, D. G. Geophysical researches with the orbits of the first satellites (англ.) // Geophysical Journal : journal. — 1983. — Vol. 74, no. 1. — P. 7—23. — doi:10.1111/j.1365-246X.1983.tb01868.x. — .
- Renzetti, G. Are higher degree even zonals really harmful for the LARES/LAGEOS frame-dragging experiment? (англ.) // Canadian Journal of Physics : journal. — 2012. — Vol. 90, no. 9. — P. 883—888. — doi:10.1139/p2012-081. — .
- Rotational Flattening. utexas.edu.