Сплюснутость
Сжатие (flattening) — мера сжатия круга или сферы по диаметру с образованием эллипса или эллипсоида соответственно вращением сфероида .
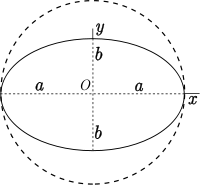
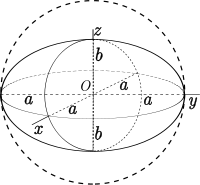
Другие используемые термины - «эллиптичность» или «сжатость». Обычное обозначение для сжатия — «f», и его определение в терминах полуосей получающегося эллипса или эллипсоида:
Коэффициент сжатия в каждом случае равен . Для эллипса этот фактор также является аспектным соотношением эллипса.
Существуют два других варианта сплюснутости, и когда необходимо избежать путаницы, указанное выше выравнивание называется первым выравниванием. Следующие определения могут встречаться в стандартных текстах[1][2][3], а также в онлайн-текстах[4][5].
Определения сплюснутости
В последующем «a» - это большее измерение (например, большая полуось), тогда как «b» - меньшее (малая полуось). Все сплющивания для круга равны нулю (a = b)
сжатие Фундаментальная. Геодезический эталонный эллипсоид указывается с помощью второе сжатие Редко используемая. третье сжатие Используется в геодезических расчетах в качестве небольшого параметра расширения.[6]
Тождества, связанные со сжатием
Сглаживание связано с другими параметрами эллипса. Например:
где - это эксцентриситет.
Числовые значения для планет
Для эллипсоида WGS84 для моделирования земли «определяющими» значениями являются[7]:
- a (экваториальный радиус): 6 378 137,0 м
- 1 / f (обратное сжатие): 298,257 223 563
из которого следует
- b (полярный радиус): 6 356 752,3142 м,
так что разница большой и вспомогательной полуосей равна 21,385 км (13 миль). (Это всего 0,335% от главной оси, поэтому представление Земли на экране компьютера будет иметь размер 300 на 299 пикселей. Поскольку это будет практически неотличимо от сферы, отображаемой как 300 на 300 пикселей, иллюстрации обычно сильно преувеличивают выравнивание в тех случаях, когда изображение должно представлять сжатие Земли.)
Другими значениями в Солнечной системе являются Юпитер, f = 1/16; Сатурн, f = 1/10, Луна f = 1/900. сжатие Солнца составляет около 9⋅10-6.
Открытие сплюснутости
В 1687 году Исаак Ньютон опубликовал « Principia», в котором он включил доказательство того, что вращающееся самогравитирующее жидкое тело в равновесии принимает форму сжатого эллипсоида революции (сфероида). Количество сглаживания зависит от плотности, баланса силы тяжести и центробежной силы.
Примечания
- Maling, Derek Hylton. Coordinate Systems and Map Projections (неопр.). — 2nd. — Oxford; New York: Pergamon Press, 1992. — ISBN 0-08-037233-3.
- Snyder, John P. Map Projections: A Working Manual (неопр.). — Washington, D.C.: United States Government Printing Office, 1987. — Т. 1395. — (U.S. Geological Survey Professional Paper).
- Torge, W. (2001). Geodesy (3rd edition). de Gruyter. ISBN 3-11-017072-8
- Osborne, P. (2008). The Mercator Projections Архивировано 18 января 2012 года. Chapter 5.
- Rapp, Richard H. (1991). Geometric Geodesy, Part I. Dept. of Geodetic Science and Surveying, Ohio State Univ., Columbus, Ohio.
- F. W. Bessel, 1825, Uber die Berechnung der geographischen Langen und Breiten aus geodatischen Vermessungen, Astron.Nachr., 4(86), 241–254, doi:10.1002/asna.201011352, translated into English by C. F. F. Karney and R. E. Deakin as The calculation of longitude and latitude from geodesic measurements, Astron. Nachr. 331(8), 852–861 (2010), E-print arXiv:0908.1824,
- html Параметры WGS84 перечислены в публикации Национального агентства геопространственной разведки TR8350.2 (недоступная ссылка), стр. 3-1.