Численная относительность
Чи́сленная относи́тельность (англ. numerical relativity) — область общей теории относительности, которая разрабатывает и использует численные методы и алгоритмы для компьютерного моделирования физических процессов в сильных гравитационных полях, когда необходимо численно решать уравнения Эйнштейна. Основные физические системы, для описания которых необходима численная относительность, относятся к релятивистской астрофизике и включают в себя гравитационный коллапс, нейтронные звёзды, чёрные дыры, гравитационные волны и другие объекты и явления, для адекватного описания которых необходимо обращаться к полной общей теории относительности без обычных приближений слабых полей и малых скоростей (как в постньютоновских разложениях и теории возмущений на фоне точных решений уравнений Эйнштейна)[1].
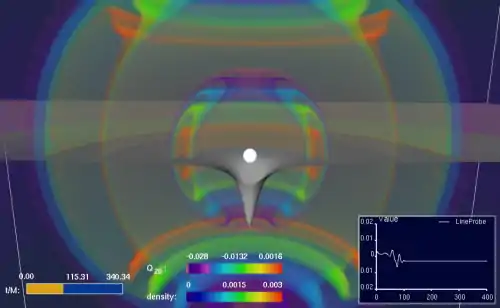
Моделирование в этой области требует специальных численных методов из-за сложности и нелинейности уравнений Эйнштейна (например, гиперболичность и корректность постановки задачи Коши их временно́й эволюции зависит от представления уравнений, а также начальных и граничных условий[2]), а также — для большинства трёхмерных задач — большой вычислительной мощности, доступной лишь современным суперкомпьютерам. На данный момент в численной относительности актуальны исследования в области моделирования релятивистских тесных двойных звёзд и связанных с ними гравитационных волн, а также многие другие математические и астрофизические проблемы[1].
Общие сведения
Главная цель численной относительности — изучение гравитационных полей, чья точная аналитическая форма неизвестна. Гравитационные поля, форма которых ищется путём вычислений, могут быть как полностью динамическими, так и стационарными или статическими, а также могут содержать материальные поля[~ 1] или быть вакуумными. В случае стационарных и статических решений численные методы могут использоваться для изучения стабильности этих конфигураций. В свою очередь, в случае динамических гравитационных полей задачу можно разделить на две части, которые требуют разных методов решения: задача начальных значений и задача эволюции[3].
Численная относительность применяется в исследованиях космологических моделей, критических явлений в гравитационном коллапсе, а также процессов с участием чёрных дыр и нейтронных звёзд, особенно их слияний и возмущений. В каждом из этих случаев необходимо прослеживать эволюцию пространства-времени, для чего уравнения Эйнштейна могут быть представлены несколькими способами. Наиболее популярными являются методы задачи Коши, однако также используются и метод характеристик[4], и методы, основанные на исчислении Редже[5]. Все перечисленные методы начинают со «снимка» гравитационного поля на некоторой гиперповерхности, то есть с начальных данных, и затем прослеживают его эволюцию до следующих близлежащих гиперповерхностей, двигаясь вперёд во времени[6].
Как и во всех задачах численного анализа, в численной относительности пристальное внимание уделяется устойчивости и сходимости численных решений, допустимым начальным и граничным условиям. Спецификой численной относительности являются усложнения, вносимые наличием калибровочных и координатных условий, а также различными представлениями уравнений Эйнштейна и их влиянием на возможность получать точные численные решения.
Многие из численных методик, применяемых в классической теории поля, неприменимы в общей теории относительности, чем работа в этой области и отличается от исследований в области численной относительности. Тем не менее, в крупномасштабных задачах численная относительность имеет много общих аспектов с другими вычислительными науками, например с вычислительной гидродинамикой, электродинамикой и механикой твёрдого тела. Учёные, занимающиеся численной относительностью, часто работают вместе с прикладными математиками и соприкасаются с такими областями математики, как численный анализ, параллельные вычисления, дифференциальные уравнения в частных производных и геометрия[7].
История
Теоретические основы
Альберт Эйнштейн опубликовал окончательную версию общей теории относительности в 1915 году[8]. Эта теория, как и предшествовавшая ей специальная теория относительности, описывает пространство и время как единый объект — пространство-время, эволюция которого подчиняется уравнениям Эйнштейна. Они образуют систему связанных нелинейных дифференциальных уравнений в частных производных. За столетие, прошедшее с вывода этих уравнений, стало известно лишь относительно небольшое число физически релевантных точных аналитических решений этих уравнений, и большинство из них выведены в предположении высокой симметрии, что упрощает решение уравнений, как, например, решения Фридмана для однородной и изотропной Вселенной[9].
Отрасль численной относительности возникла из желания изучать более общие и физически приложимые решения уравнений Эйнштейна, приближённо решая их численно. Необходимым условием для такого их решения было проведение расщепления единого четырёхмерного пространства-времени обратно на разделённые трёхмерное пространство и одномерное время, так называемое 3+1 расщепление. При этом оно может быть проведено множеством различных путей, которые способны существенно усложнить или упростить задачу интегрирования результирующих уравнений. Первая вполне успешная попытка расщепления была проделана Ричардом Арновиттом, Стенли Дезером и Чарльзом Мизнером в конце 1950-х в гамильтоновом формализме на пути, указанном Дираком. Она увенчалась получением уравнений, образующих так называемый АДМ-формализм — формализм Арновитта — Дезера — Мизнера[10]. Хотя по техническим причинам именно эти уравнения оказались не очень удобными для численного интегрирования — они лишь слабо гиперболичны и поэтому редко используются в реальных вычислениях — подавляющее большинство практических подходов к численной относительности используют 3+1 расщепление, близкое к тому, которое использовалось в АДМ-формализме. Такое расщепление ведёт к переформулировке уравнений Эйнштейна в виде задачи Коши с ограничениями на начальные значения, что уже поддаётся численному решению на компьютерах[11].
Координаты в пространстве-времени не могут быть определены однозначно, поэтому даже при фиксировании координат на начальной гиперповерхности, при переходе к соседней гиперповерхности время и пространственные координаты можно «толкать» по-разному в различных точках (уже в специальной теории относительности направление и скорость течения времени не совпадает в различных инерциальных системах отсчёта), что является спецификой численной относительности. Эта калибровочная свобода — не влияющая на физические процессы, а лишь изменяющая их описание в терминах координат и, соответственно, решаемые уравнения — проявляется в произвольности выбора функций хода и сдвига , «толкающих» точки с фиксированными пространственными координатами с начальной на соседнюю гиперповерхность вперёд по времени — , и вбок в пространстве — , соответственно. Возможность выбора этих функций — потенциальное преимущество для численного решения уравнений, но многие «естественные» выборы этих координатных или калибровочных условий, как оказалось, вызывают численные неустойчивости решений, приводя к обрыву моделирований[12].

Во время публикации исходных работ по АДМ-формализму развитие компьютерной техники не позволяло проводить расчёты по их уравнениям для любой задачи сколь-нибудь разумных размеров. Исторически первая попытка численного решения уравнений Эйнштейна была предпринята Хан и Линдквистом в 1964 году[13], а затем в 1970-х годах Смарром[14][15] и Эппли[16]. Эти ранние попытки были связаны с эволюцией начальных данных Мизнера в аксиально-симметричных пространствах (известных также как «2+1-мерие»). Примерно в это же время Цви Пиран написал первый код, который прослеживал эволюцию цилиндрически-симметричной системы, испускающей гравитационное излучение[17]. В этой разработке Пиран положил начало многим концепциям, используемым ныне в численной относительности, таким как свободная эволюция (free evolution) и ограниченная эволюция (constrained evolution) — это методы, которые по-разному подходят к проблеме эволюции ограничений начальных данных во времени[18][19]. Применение симметрии снизило необходимые требования к памяти и вычислительной мощности, позволив учёным использовать для решения этой задачи тогдашние суперкомпьютеры[17].
Ранние результаты
Первые реалистичные вычисления для настоящей астрофизической задачи — коллапса с вращением, были проведены в начале 1980-х годов Ричардом Старком и Цви Пираном[20], в них были впервые рассчитаны гравитационные волны, излучаемые формирующейся вращающейся чёрной дырой. За почти два десятилетия, прошедшие после этой публикации, были обнародованы лишь несколько новых результатов в области численной относительности, вероятно, из-за недостатка достаточно мощных для решения этих проблем компьютеров. В 1990-х Альянс «Великого вызова» по двойным чёрным дырам (англ. Binary Black Hole Grand Challenge Alliance) успешно моделировал лобовое столкновение двух чёрных дыр, используя упрощения, возникающие из-за аксиальной симметрии задачи. На этапе постобработки группа смогла вычислить горизонт событий для полученного решения[21].
Некоторые из первых известных попыток численных решений уравнений Эйнштейна в полной трёхмерной пространственной геометрии фокусировались на невращающейся шварцшильдовской чёрной дыре, которая представляет собой статическое и сферически-симметричное решение уравнений Эйнштейна. Оно представляет собой прекрасный тест для методов численной относительности, так как, во-первых, решение известно в точной аналитической форме, с которой можно сравнивать численные результаты, во-вторых, оно статическое и к нему должна сходиться любая невращающаяся чёрная дыра с течением времени, а в-третьих, оно содержит один из самых сложных объектов для численного моделирования — физическую гравитационную сингулярность в центре. Одна из первых попыток получить это решение численно была предпринята Анниносом и соавторами в 1995 году[22]. В этой работе они отмечали:
Прогресс в трёхмерной численной относительности частично замедляется отсутствием компьютеров с памятью и вычислительной мощностью, достаточной для проведения вычислений в трёхмерном пространстве с хорошим разрешением.
Оригинальный текст (англ.)[показатьскрыть]Progress in three dimensional numerical relativity has been impeded in part by lack of computers with sufficient memory and computational power to perform well resolved calculations of 3D spacetimes.
Развитие области
За последующие годы помимо того, что компьютеры стали более мощными, различными исследовательскими группами были разработаны альтернативные техники для повышения эффективности вычислений. Сначала группа Lazarus разработала методы, которые использовали ранние результаты коротких моделирований, решавших нелинейные АДМ-уравнения для слияния чёрных дыр, для того, чтобы обеспечить начальные данные для более устойчивого кода, основанного на линеаризированных уравнениях теории возмущений одиночной чёрной дыры[23]. Затем в отношении моделирования чёрных дыр были разработаны две техники, позволяющие избежать проблем, связанных с существованием физической сингулярности в решениях уравнений: (1) исключение и (2) метод «уколов»[24]. Сочетание этих методов с найденными подходящими координатными условиями позволило в 2005 году совершить прорыв в моделировании двойных чёрных дыр, началом которого была работа Преториуса[25]. Через несколько лет численная устойчивость новых методов позволила моделировать уже практически произвольные конфигурации двойных чёрных дыр, описывающих до слияния десятки и сотни оборотов друг вокруг друга. Кроме того, в численной относительности стали применяться методы адаптивного измельчения расчётной сетки, которые ранее уже использовались в вычислительной гидродинамике[26].
Проект Lazarus
Проект Lazarus (1998—2005) был разработан после «Великого вызова» как методика извлечения астрофизически релевантных результатов из доступных на то время коротких численных моделирований процессов слияния двойных чёрных дыр. Тогда все известные попытки интегрировать на суперкомпьютерах уравнения Эйнштейна для пространства-времени двойных чёрных дыр из-за различного рода нестабильностей не были способны продвинуться даже до завершения одного полного оборота системы. В рамках проекта исследователи сочетали приблизительные методы до (постньютоновские траектории) и после превращения пары дыр в одну (возмущения одиночных чёрных дыр) с полными численными решениями самого процесса[23].
Подход проекта Lazarus на то время был наилучшим подходом к проблеме двойных чёрных дыр и дал большое количество достаточно точных для астрофизических приложений результатов, таких как величины уносимых гравитационными волнами энергии и углового момента[27][28], а также импульса при слиянии чёрных дыр различных масс[29], и значения финальной массы, импульса и углового момента возникающей чёрной дыры[30]. Методы проекта также позволили рассчитать детальные формы гравитационных волн, излучаемых в процессе слияния — что было важно для гравитационных телескопов, и предсказали, что столкновения чёрных дыр должны сопровождаться наиболее мощными выплесками энергии во Вселенной, когда за доли секунды высвобождается в виде гравитационного излучения больше энергии, чем излучают все звёзды галактики за время её существования — гравитационное излучение уносит несколько процентов начальной приведённой массы системы[31].
Метод исключения
В методике исключения (англ. excision technique), которая была впервые предложена в конце 1990-х[32], часть пространства-времени внутри горизонта событий, окружающая сингулярность чёрной дыры, просто исключается из эволюции. Теоретически это не должно влиять на решение вне горизонта событий из-за принципа причинности и свойств горизонта — так как никакие физические взаимодействия под горизонтом не могут оказывать никакого воздействия на физику вне его. Таким образом, если просто не решать уравнений внутри чёрной дыры, вне её всё равно можно получить точное реальное решение. Можно «исключить» внутреннюю динамику, наложив на границу внутри горизонта, охватывающую сингулярность, граничные условия отсутствия исходящих волн[33].
Хотя использование техники исключения было весьма успешным, она имеет две небольшие проблемы. Первая состоит в том, что нужно аккуратно выбирать и использовать координатные условия. В то время как физические эффекты не могут распространяться изнутри горизонта наружу, координатные эффекты могут. Например, если накладывать эллиптические координатные условия, изменения координатной сетки внутри чёрной дыры могут мгновенно распространяться наружу через горизонт[34]. Это означает, что для применения метода исключения нужно использовать координатные условия гиперболического типа, характеристические скорости распространения координатных эффектов в которых меньше или равны скорости света (например, используя гармонические координатные условия)[35]. Вторая проблема заключается в том, что поскольку чёрная дыра движется, область исключения необходимо постоянно двигать согласованно с ней[33].
Метод исключения разрабатывался несколько лет, при этом были найдены новые калибровочные условия, увеличивающие стабильность процедуры решения, и продемонстрирована способность исключённых регионов двигаться по вычислительной сетке[36][37][38][39][40][35]. Первое стабильное длинное вычисление орбиты и слияния двух чёрных дыр с помощью этой методики было опубликовано в 2005 году[25].
Метод «уколов»
В методе «уколов» (англ. puncture method) решение делится на аналитическую часть[41], которая содержит сингулярность чёрной дыры — укол, и на часть, построенную численно, которая сингулярности не содержит. Этот метод является обобщением алгоритма Брилла — Линдквиста[42] для начальных данных с чёрными дырами в покое, и может быть далее обобщён на алгоритм Боуена — Йорка[43] для начальных данных с вращающимися и движущимися чёрными дырами. До 2005 года во всех опубликованных примерах использования метода «уколов» требовалось, чтобы координаты всех уколов были фиксированными на протяжении всего времени действия моделирования. Конечно, чёрные дыры, находясь в непосредственной близости друг от друга, будут двигаться под воздействием гравитационных сил, таким образом, фиксированные координаты уколов означают, что системы координат становятся «растянутыми» или «искажёнными», что приводит к численной неустойчивости на некоторых этапах моделирования. Аналогичные эффекты вызывает использование другого метода — избегания сингулярностей, когда чёрные дыры формируют в моделировании путём коллапса материи, а координатные условия выбираются таким образом, чтобы эволюционирующая во времени трёхмерная гиперповерхность не доходила до сингулярности до конца вычислений, формируя вытянутый «рог» вокруг неё[44].
В 2005 году исследователи впервые продемонстрировали возможность движения уколов по системе координат, таким образом решив некоторые из ранних проблем метода, что позволило точно прослеживать долговременную эволюцию чёрных дыр[25][45][46]. Выбрав подходящие координатные условия и сделав грубые аналитические приближения физических полей вблизи сингулярности (так как никакие физические эффекты не могут выходить наружу из чёрной дыры, грубость аппроксимации не важна), можно получить численные решения для задачи о двух чёрных дырах, вращающихся друг вокруг друга, а также точно вычислить их гравитационное излучение[47].
Адаптивное измельчение расчётной сетки
Адаптивное измельчение расчётной сетки как численный метод применялось в физике задолго до расцвета численной относительности. В ней оно впервые было использовано в 1980-х годах в работах Чоптуика при изучении критических явлений в процессе коллапса скалярного поля, когда конфигурации поля находятся на самой грани между финальным образованием чёрной дыры и финальным разлётом в пространстве[48][49]. Исходные работы были одномерными, так как использовали сферическую симметрию, но затем метод был обобщён до двух измерений[50]. Двумерные методы измельчения были также применены к изучению неоднородных космологий[51][52] и шварцшильдовских чёрных дыр[53]. Сейчас методы адаптивного измельчения стали стандартным инструментом в численной относительности и используются в изучении слияний чёрных дыр и других компактных объектов, в дополнение к изучению распространения гравитационных волн, порождаемых такими событиями[54][55].
Современное развитие

По настоящее время по численной относительности пишутся десятки и сотни статей в год, представляющих широкий спектр результатов в областях математики общей теории относительности, гравитационных волн и астрофизики, полученных при решении задачи о вращающихся друг вокруг друга чёрных дырах. Использованные при этом методы были обобщены для изучения астрофизических бинарных систем, включающих в себя нейтронные звёзды, чёрные дыры[56] и множества чёрных дыр[57]. Среди прочего, в этих работах предсказывается, что при слиянии двух вращающихся чёрных дыр получившаяся дыра может развивать скорость до 4000 и даже до 10 000 км/c, что позволяет ей выйти за пределы любой известной галактики[58][59]. Моделирования также предсказывают огромный выброс энергии при слиянии, который может составить до 8 % общей массы в покое, и возможность резкого изменения оси вращения чёрной дыры, что может объяснять наблюдаемые в радиогалактиках изменения направлений джетов[60]. Важным направлением исследований является также создание каталога форм гравитационного излучения сливающихся чёрных дыр, без которого поиск этих сигналов в данных с детекторов типа LIGO и VIRGO обладает много меньшей чувствительностью[61].
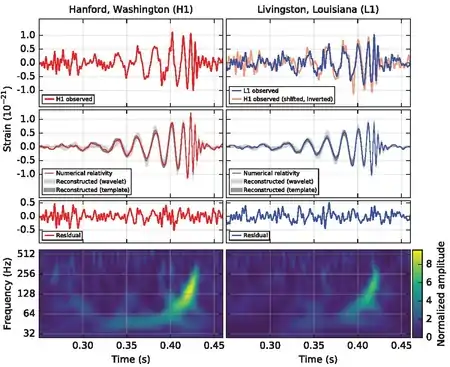
Точность современных методов численной относительности стало возможно проверить на практике непосредственно после открытия гравитационных волн. Сигнал GW150914 оказался совпадающим с предсказаниями численной относительности в пределах 4 % погрешности[62].
См. также
- Математическая формулировка общей теории относительности
- Постньютоновское разложение
- Переворот оси вращения
- Фреймворк Cactus
Примечания
- В общей теории относительности все поля, кроме гравитационного, принято называть материальными.
- Источники
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Preface. Sec. What is numerical relativity?.
- Choptuik M. W. Computational Methods in General Relativity: The Theory, 2006.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Sec. 2.6 The constraint and evolution equations and Introduction of Ch. 3 Constructing initial data.
- Winicour J. Characteristic Evolution and Matching (англ.) // Living Reviews in Relativity. — 2012. — Vol. 15, no. 2. — doi:10.12942/lrr-2012-2. — . Архивировано 15 августа 2015 года.
- Gentle Adrian P. Regge Calculus: A Unique Tool for Numerical Relativity (англ.) // General Relativity and Gravitation. — 2002. — Vol. 34, iss. 10. — P. 1701—1718. — ISSN 0001-7701. — doi:10.1023/A:1020128425143.
- Cook G. Initial Data for Numerical Relativity (англ.) // Living Reviews in Relativity. — 2000. — Vol. 3, no. 5. — doi:10.12942/lrr-2000-5. — . — arXiv:gr-qc/0007085. Архивировано 12 июля 2006 года.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Ch. 6 Numerical methods.
- Albert Einstein. Der Feldgleichungen der Gravitation. — Sitzungsberiche der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik.
- Stephani H., Kramer D., MacCallum M., Hoenselaers C., Herlt E. Sec. 1.1 What are exact solutions, and why study them? // Exact Solutions of Einstein's Field Equations (англ.). — Cambridge University Press, 2003. — (Cambridge Monographs on Mathematical Physics). — ISBN 9781139435024.
- Arnowitt R., Deser S., Misner C. W. The dynamics of general relativity // Gravitation: An Introduction to Current Research / Ed. by L. Witten. — New York: Wiley, 1962. — С. 227—265.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Ch. 2 The 3+1 decompostion of Einstein’s equations.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Ch. 4 Choosing coordinates: the lapse and shift.
- Hahn S. G., Lindquist R. W. The two-body problem in geometrodynamics // Annals of Physics. — 1964. — Т. 29. — С. 304—331. — doi:10.1016/0003-4916(64)90223-4. — .
- Smarr, Larry. The Structure of General Relativity with a Numerical Example (англ.). — Ph.D. Dissertation, University of Texas, Austin. — Austin, Texas, 1975.
- Smarr L. Spacetimes generated by computers: Black holes with gravitational radiation // N. Y. Acad. Sci. — 1977. — Т. 302. — С. 569. — doi:10.1111/j.1749-6632.1977.tb37076.x.
- Eppley, K. The numerical evolution of the collision of two black holes (англ.). — Ph.D. Dissertation, Princeton University. — Princeton, New Jersey, 1975.
- Piran T. Cylindrical general relativistic collapse // Phys. Rev. Lett. — 1978. — Т. 41, вып. 16. — С. 1085. — doi:10.1103/PhysRevLett.41.1085. — .
- Alcubierre M. Introduction to 3+1 Numerical Relativity, 2008, Sec. 2.6 Free versus constrained evolution.
- Bona C., Palenzuela-Luque C., Bona-Casas C. Elements of Numerical Relativity and Relativistic Hydrodynamics, 2009, Subsec. 2.3.3 Evolution strategies.
- Stark R. F., Piran T. Gravitational-wave emission from rotating gravitational collapse // Physical Review Letters. — 1985. — Т. 55. — С. 891—894. — doi:10.1103/PhysRevLett.55.891. — .
- Matzner R. A., Seidel H. E., Shapiro S. L., Smarr L., Suen W.-M., Teukolsky S. A., Winicour J. Geometry of a Black Hole Collision (англ.) // Science. — 1995. — Vol. 270, iss. 5238. — P. 941—947. — doi:10.1126/science.270.5238.941. — .
- Anninos P., Massó J., Seidel E., Suen W.-M., Towns J. Three-dimensional numerical relativity: The evolution of black holes // Physical Review D. — 1995. — Т. 52, вып. 4. — С. 2059—2082. — doi:10.1103/PhysRevD.52.2059. — . — arXiv:gr-qc/9503025.
- Baker J., Campanelli M., Lousto C. O. The Lazarus project: A pragmatic approach to binary black hole evolutions // Physical Review D. — 2002. — Т. 65, вып. 4. — С. 044001. — doi:10.1103/PhysRevD.65.044001. — . — arXiv:gr-qc/0104063.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Ch. 13 Binary black hole evolution.
- Pretorius F. Evolution of Binary Black-Hole Spacetimes // Physical Review Letters. — 2005. — Т. 95, вып. 12. — С. 121101. — doi:10.1103/PhysRevLett.95.121101. — . — arXiv:gr-qc/0507014.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Subsec. 6.2.5 Mesh refinement.
- Baker J., Brügmann B., Campanelli M., Lousto C. O., Takahashi R. Plunge Waveforms from Inspiralling Binary Black Holes // Physical Review Letters. — 2001. — Т. 87, вып. 12. — С. 121103. — doi:10.1103/PhysRevLett.87.121103. — . — arXiv:gr-qc/0102037.
- Baker J., Campanelli M., Lousto C. O., Takahashi R. Modeling gravitational radiation from coalescing binary black holes // Physical Review D. — 2002. — Т. 65, вып. 12. — С. 124012. — doi:10.1103/PhysRevD.65.124012. — . — arXiv:astro-ph/0202469.
- Campanelli M. Understanding the fate of merging supermassive black holes // Classical and Quantum Gravity. — 2005. — Т. 22. — С. 387. — doi:10.1088/0264-9381/22/10/034. — . — arXiv:astro-ph/0411744.
- Baker J., Campanelli M., Lousto C. O., Takahashi R. Coalescence remnant of spinning binary black holes // Physical Review D. — 2004. — Т. 69, вып. 2. — С. 027505. — doi:10.1103/PhysRevD.69.027505. — . — arXiv:astro-ph/0305287.
- Berti E., Cardoso V., Gonzalez J. A., Sperhake U., Hannam M., Husa S., Brügmann B. Inspiral, merger, and ringdown of unequal mass black hole binaries: A multipolar analysis (англ.) // Physical Review D. — 2007. — Vol. 76, iss. 6. — P. 064034 (1—40). — doi:10.1103/PhysRevD.76.064034. — . — arXiv:gr-qc/0703053.
- Alcubierre M., Brügmann B. Simple excision of a black hole in 3+1 numerical relativity // Physical Review D. — 2001. — Т. 63, вып. 10. — С. 104006. — doi:10.1103/PhysRevD.63.104006. — . — arXiv:gr-qc/0008067.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Subsec. 13.1.2 Black hole excision.
- Bona C., Palenzuela-Luque C., Bona-Casas C. Elements of Numerical Relativity and Relativistic Hydrodynamics, 2009, Subsec. 6.1.3 Regular initial data.
- Shoemaker D., Smith K., Sperhake U., Laguna P., Schnetter E., Fiske D. Moving black holes via singularity excision // Classical and Quantum Gravity. — 2003. — Т. 20, вып. 16. — С. 3729—3743. — doi:10.1088/0264-9381/20/16/313. — . — arXiv:gr-qc/0301111.
- C. Bona, J. Masso, E. Seidel, J. Stela. New formalism for numerical relativity // Phys. Rev. Lett.. — 1995. — Т. 75, вып. 4. — С. 600—603. — doi:10.1103/PhysRevLett.75.600. — . — arXiv:gr-qc/9412071.
- Cook G. B., Huq M. F., Klasky S. A., Scheel M. A., Abrahams A. M., Anderson A., Anninos P., Baumgarte T. W., Bishop N. T., Brandt S. R., Browne J. C., Camarda K., Choptuik M. W., Correll R. R., Evans C. R., Finn L. S., Fox G. C., Gómez R., Haupt T., Kidder L. E., Laguna P., Landry W., Lehner L., Lenaghan J., Marsa R. L., Masso J., Matzner R. A., Mitra S., Papadopoulos P., Parashar M., Rezzolla L., Rupright M. E., Saied F., Saylor P. E., Seidel E., Shapiro S. L., Shoemaker D., Smarr L., Suen W. M., Szilágyi B., Teukolsky S. A., van Putten M. H., Walker P., Winicour J., York J. W. Boosted Three-Dimensional Black-Hole Evolutions with Singularity Excision // Physical Review Letters. — 1998. — Т. 80. — С. 2512—2516. — doi:10.1103/PhysRevLett.80.2512. — . — arXiv:gr-qc/9711078.
- Alcubierre M. Hyperbolic slicings of spacetime: singularity avoidance and gauge shocks // Classical and Quantum Gravity. — 2003. — Т. 20. — С. 607—623. — . — arXiv:gr-qc/0210050.
- Alcubierre M., Brügmann B., Diener P., Koppitz M., Pollney D., Seidel E., Takahashi R. Gauge conditions for long-term numerical black hole evolutions without excision // Physical Review D. — 2003. — Т. 67, вып. 8. — С. 084023. — doi:10.1103/PhysRevD.67.084023. — . — arXiv:gr-qc/0206072.
- Brügmann B., Tichy W., Jansen N. Numerical Simulation of Orbiting Black Holes // Physical Review Letters. — 2004. — Т. 92, вып. 21. — С. 211101. — doi:10.1103/PhysRevLett.92.211101. — . — arXiv:gr-qc/0312112.
- Brandt S., Brügmann B. A Simple Construction of Initial Data for Multiple Black Holes // Physical Review Letters. — 1997. — Т. 78, вып. 19. — С. 3606—3609. — doi:10.1103/PhysRevLett.78.3606. — . — arXiv:gr-qc/9703066.
- Brill D. R., Lindquist R. W. Interaction Energy in Geometrostatics // Physical Review. — 1963. — Т. 131, вып. 1. — С. 471—476. — doi:10.1103/PhysRev.131.471. — .
- Bowen J. M., York Jr., J. W. Time-asymmetric initial data for black holes and black-hole collisions // Physical Review D. — 1980. — Т. 21, вып. 8. — С. 2047—2056. — doi:10.1103/PhysRevD.21.2047. — .
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Subsec. 13.1.1 Singularity avoiding coordinates.
- Baker J. G., Centrella J., Choi D.-I., Koppitz M., van Meter J. Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes // Physical Review Letters. — 2006. — Т. 96, вып. 11. — С. 111102. — doi:10.1103/PhysRevLett.96.111102. — . — arXiv:gr-qc/0511103.
- Campanelli M., Lousto C. O., Marronetti P., Zlochower Y. Accurate Evolutions of Orbiting Black-Hole Binaries without Excision // Physical Review Letters. — 2006. — Т. 96, вып. 11. — С. 111101. — doi:10.1103/PhysRevLett.96.111101. — . — arXiv:gr-qc/0511048.
- Baumgarte T. W., Shapiro S. L. Numerical Relativity, 2010, Subsec. 13.1.3 The moving puncture method.
- Choptuik, M. W. Experiences with an adaptive mesh refinement algorithm in numerical relativity // Frontiers in numerical relativity / Evans, C.; Finn, L.; Hobill, D.. — Cambridge: Cambridge University Press, 1989. — ISBN 0521366666.
- Choptuik M. W. Universality and scaling in gravitational collapse of a massless scalar field // Physical Review Letters. — 1993. — Т. 70, вып. 1. — С. 9—12. — doi:10.1103/PhysRevLett.70.9. — .
- Choptuik M. W., Hirschmann E. W., Liebling S. L., Pretorius F. Critical collapse of the massless scalar field in axisymmetry // Physical Review D. — 2003. — Т. 68, вып. 4. — С. 044007. — doi:10.1103/PhysRevD.68.044007. — . — arXiv:gr-qc/0305003.
- Hern, Simon David. Numerical relativity and inhomogeneous cosmologies (англ.). — Ph.D. Dissertation, Cambridge University, 1999.
- Belanger, Z. B. Adaptive mesh refinement in the T2 symmetric spacetime (англ.). — Master's Thesis, Oakland University, 2001.
- Schnetter E., Hawley S. H., Hawke I. Evolutions in 3D numerical relativity using fixed mesh refinement // Classical and Quantum Gravity. — 2004. — Т. 21. — С. 1465—1488. — doi:10.1088/0264-9381/21/6/014. — . — arXiv:gr-qc/0310042.
- Imbiriba B., Baker J., Choi D.-I., Centrella J., Fiske D. R., Brown J. D., van Meter J. R., Olson K. Evolving a puncture black hole with fixed mesh refinement // Physical Review D. — 2004. — Т. 70, вып. 12. — С. 124025. — doi:10.1103/PhysRevD.70.124025. — . — arXiv:gr-qc/0403048.
- Fiske D. R., Baker J. G., van Meter J. R., Choi D.-I., Centrella J. M. Wave zone extraction of gravitational radiation in three-dimensional numerical relativity // Physical Review D. — 2005. — Т. 71, вып. 10. — С. 104036. — doi:10.1103/PhysRevD.71.104036. — . — arXiv:gr-qc/0503100.
- Etienne Z. B., Liu Y. T., Shapiro S. L., Baumgarte T. W. General relativistic simulations of black-hole-neutron-star mergers: Effects of black-hole spin // Physical Review D. — 2009. — Т. 79, вып. 4. — С. 044024. — doi:10.1103/PhysRevD.79.044024. — . — arXiv:0812.2245.
- Lousto C. O., Zlochower Y. Foundations of multiple-black-hole evolutions // Physical Review D. — 2008. — Т. 77, вып. 2. — С. 024034. — doi:10.1103/PhysRevD.77.024034. — . — arXiv:0711.1165.
- Campanelli M., Lousto C. O., Zlochower Y., Merritt D. Maximum Gravitational Recoil // Physical Review Letters. — 2007. — Т. 98, вып. 23. — С. 231102. — doi:10.1103/PhysRevLett.98.231102. — . — arXiv:gr-qc/0702133.
- Healy J., Herrmann F., Hinder I., Shoemaker D. M., Laguna P., Matzner R. A. Superkicks in Hyperbolic Encounters of Binary Black Holes // Physical Review Letters. — 2009. — Т. 102, вып. 4. — С. 041101. — doi:10.1103/PhysRevLett.102.041101. — . — arXiv:0807.3292.
- Campanelli M., Lousto C. O., Zlochower Y., Krishnan B., Merritt D. Spin flips and precession in black-hole-binary mergers // Physical Review D. — 2007. — Т. 75, вып. 6. — С. 064030. — doi:10.1103/PhysRevD.75.064030. — . — arXiv:gr-qc/0612076.
- Hinder I., Buonanno A., Boyle M., Etienne Z. B., Healy J., Johnson-McDaniel N. K., Nagar A., Nakano H., Pan Y., Pfeiffer H. P., Pürrer M., Reisswig C., Scheel M. A., Schnetter E., Sperhake U., Szilágyi B., Tichy W., Wardell B., Zenginoğlu A., Alic D., Bernuzzi S., Bode T., Brügmann B., Buchman L. T., Campanelli M., Chu T., Damour T., Grigsby J. D., Hannam M., Haas R., Hemberger D. A., Husa S., Kidder L. E., Laguna P., London L., Lovelace G., Lousto C. O., Marronetti P., Matzner R. A., Mösta P., Mroué A., Müller D., Mundim B. C., Nerozzi A., Paschalidis V., Pollney D., Reifenberger G., Rezzolla L., Shapiro S. L., Shoemaker D., Taracchini A., Taylor N. W., Teukolsky S. A., Thierfelder M., Witek H., Zlochower Y. Error-analysis and comparison to analytical models of numerical waveforms produced by the NRAR Collaboration // Classical and Quantum Gravity. — 2013. — Т. 31, вып. 2. — С. 025012. — doi:10.1088/0264-9381/31/2/025012. — . — arXiv:1307.5307.
- The LIGO Scientific Collaboration, the Virgo Collaboration. Tests of general relativity with GW150914 (англ.) // ArXiv e-prints. — 2016. — . — arXiv:1602.03841. Архивировано 15 февраля 2016 года.
Литература
- Энциклопедии
- Choptuik M. W. Computational Methods in General Relativity: The Theory (англ.) // Encyclopedia of mathematical physics / Ed. by Françoise J. P., Naber G. L., Tsun T. S. — Elsevier, 2006. — Vol. 1. — P. 604—610. — ISBN 9780125126601.
- Учебники
- Baumgarte T. W., Shapiro S. L. Numerical Relativity: Solving Einstein's Equations on the Computer. — Cambridge University Press, 2010. — ISBN 9780521514071.
- Alcubierre M. Introduction to 3+1 Numerical Relativity (англ.). — Oxford University Press, 2008. — ISBN 9780199205677.
- Bona C., Palenzuela-Luque C., Bona-Casas C. Elements of Numerical Relativity and Relativistic Hydrodynamics: From Einstein's Equations to Astrophysical Simulations. — 2-е изд. — Springer-Verlag, 2009. — (Lecture Notes in Physics, Том 783). — ISBN 9783642011634.
- Gourgoulhon E. 3+1 Formalism in General Relativity: Bases of Numerical Relativity. — Springer-Verlag, 2012. — (Lecture Notes in Physics, Том 846). — ISBN 9783642245244.
Ссылки
- Обзоры
- Cook G. Initial Data for Numerical Relativity (англ.) // Living Reviews in Relativity. — 2000. — Vol. 3, no. 5. — doi:10.12942/lrr-2000-5. — . — arXiv:gr-qc/0007085. — Обзорная статья с детальным обсуждением численной относительности.
- Stergioulas N. Rotating Stars in Relativity (англ.) // Living Reviews in Relativity. — 2003. — Vol. 6, no. 3. — doi:10.12942/lrr-2003-3. — . — arXiv:gr-qc/0302034. — Техничная обзорная статья о вращающихся звёздах с разделом о применениях численной относительности.
- Fryer C. L., New K. C. B. Gravitational Waves from Gravitational Collapse (англ.) // Living Reviews in Relativity. — 2011. — Vol. 14, no. 1. — doi:10.12942/lrr-2011-1. — . — Обзор методов и результатов моделирования гравитационных волн от коллапса.
- Shibata M., Taniguchi K. Coalescence of Black Hole-Neutron Star Binaries (англ.) // Living Reviews in Relativity. — 2011. — Vol. 14, no. 6. — doi:10.12942/lrr-2011-6. — . — Обзор физических процессов в процессе поглощения нейтронной звезды чёрной дырой и их численного моделирования, а также полученных результатов симуляций.
- Winicour J. Characteristic Evolution and Matching (англ.) // Living Reviews in Relativity. — 2012. — Vol. 15, no. 2. — doi:10.12942/lrr-2012-2. — . — Обзор перспективной методики решения уравнений Эйнштейна не в виде задачи Коши, а в виде задачи с начальными значениями на характеристиках, что позволяет непосредственно извлекать формы гравитационно-волнового сигнала из численных симуляций.
- Faber J. A., Rasio F. A. Binary Neutron Star Mergers (англ.) // Living Reviews in Relativity. — 2012. — Vol. 15, no. 8. — doi:10.12942/lrr-2012-8. — . — arXiv:1204.3858. — Обзор физических процессов в слияниях нейтронных звёзд и их численного моделирования, а также полученных результатов симуляций.
- Sarbach O., Tiglio M. Continuum and Discrete Initial-Boundary Value Problems and Einstein's Field Equations (англ.) // Living Reviews in Relativity. — 2012. — Vol. 15, no. 9. — doi:10.12942/lrr-2012-9. — . — arXiv:1203.6443. — Обзор проблемы начальных значений и проблемы представления непрерывных уравнений Эйнштейна сеточной дискретной их версией.
- Разное
- A Relativity Tutorial at Caltech — Вводный курс основных концепций численной относительности.
- Численная относительность на arXiv.