Чередующаяся перестановка

Чередующаяся перестановка[1] (перестановка down-up; иногда альтернирующая перестановка от англ. alternating permutation или пилообразная перестановка) — перестановка $a$ , такая что её члены по очереди возрастают и убывают, начиная с убывания:

a_{1}>a_{2}<a_{3}>a_{4}<\ldots

.

$n$	Чередующиеся перестановки	Обратно чередующиеся перестановки	Количество $A_{n}$
2	(2,1)	(1,2)	2
3	(2,1,3), (3,1,2)	(1,3,2), (2,3,1)	4
4	(2,1,4,3), (3,1,4,2), (3,2,4,1), (4,1,3,2), (4,2,3,1)	(1,3,2,4), (1,4,2,3), (2,3,1,4), (2,4,1,3), (3,4,1,2)	10

Геометрическое изображение всех чередующихся перестановок пяти элементов. Перестановки лексикографически упорядочены — от (1,3,2,5,4) (сверху слева) до (4,5,2,3,1) (снизу справа).

Обратно чередующаяся перестановка (перестановка up-down) $a$ — такая, что её члены по очереди возрастают и убывают, начиная с возрастания:

a_{1}<a_{2}>a_{3}<a_{4}>\ldots

.

Иногда условие того, начинается ли чередование с возрастания или убывания, опускают, и оба варианта называют чередующимися перестановками без уточнения.

Симметрии

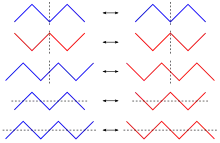
Горизонтальное и вертикально отражений чередующихся (красных) и обратно чередующихся (синих) перестановок.

Чередующиеся перестановки могут быть изображены геометрически как пилообразная кривая (см. рисунок справа). На них существует два биективных отображения — отражение относительно горизонтали или вертикали. При этом горизонтальное отражение переводит чередующиеся в чередующиеся для нечётной длины и в обратно чередующиеся для чётной, а вертикальное — всегда в обратно чередующиеся. В частности, число чередующихся и число обратно чередующихся перестановок на одном количестве элементов одинаково[2].

Количество перестановок

Числа $A_{n}$ чередующихся перестановок на $n$ элементах образуют последовательность, начинающуюся c 1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, 50521, …, см. последовательность A000111 в OEIS.

Разбивая чередующиеся или обратно чередующиеся перестановки по положению элемента $1$ , можно показать, что эта последовательность удовлетворяет рекуррентному соотношению[1]

2A_{n+1}=\sum _{i=0}^{n}{\binom {n}{i}}A_{i}A_{n-i}

.

Таким образом, экспоненциальная производящая функция $A(x)=\sum _{n\geq 0}A_{n}x^{n}/n!$ этой последовательности удовлетворяет дифференциальному уравнению

2A'(x)=1+(A(x))^{2}

с начальным условием $A(0)=1$ [3]. Из этого можно вывести, что она равна $A(x)=\mathrm {tg} x+\sec x$ [1].

Секанс чётен, а тангенс — нечётен, поэтому чётные члены последовательности совпадают с коэффициентами в ряде Тейлора секанса, а нечётные — тангенса, а потому выражаются через числа Бернулли и числа Эйлера соответственно, см. подробности в Тригонометрические функции#Определение тригонометрических функций через ряды.

Ассимптотически последовательность $A_{n}$ равна

{\frac {A_{n}}{n!}}\simeq 2\left({\frac {2}{\pi }}\right)^{n+1}

.

Число справа примерно равно вероятности того, что перестановка чередующаяся[4].

Числа Энтрингера

Число $A_{n,k}$ чередующихся перестановок $n$ элементов, начинающихся с $k$
${}_{n}\!\diagdown \!\!{}^{k}$	1	2	3	4	5	6	7	$A_{n}$
2	0	1						1
3	0	1	1					2
4	0	1	2	2				5
5	0	2	4	5	5			16
6	0	5	10	14	16	16		61
7	0	16	32	46	56	61	61	272

Числа Энтрингера (англ. Entringer numbers) — это числа $A_{n,k}$ чередующихся перестановок $n$ элементов, начинающихся с $k$ . Таким образом,

A_{n}=\sum _{k=1}^{n}A_{n,k}

.

Кроме того, поскольку к любой обратно чередующейся последовательности можно прибавить в начале $(n+1)$ , и получить чередующуюся последовательность,

A_{n+1,n+1}=A_{n}

,

а потому числа чередующихся последовательностей — частный случай чисел Энтрингера.

Числа Энтрингена удовлетворяют рекуррентному соотношению

A_{n,k}=A_{n,k-1}+A_{n-1,n-k+1}

и потому образуют треугольник наподобие треугольника Паскаля (см. справа). Последовательность, получающаяся при его построчном перечислении с пропуском нулей, — это последовательность A008282 в OEIS[5].

Примечания

Р. Стенли Перечислительная комбинаторика. — Рипол Классик. — С. 219. — ISBN 9785458261043.
Stanley, Richard P. Enumerative Combinatorics (неопр.). — 2nd. — Cambridge University Press, 2011. — Т. I.
Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, с. 2
Folkmar Bornemann. Konkrete Analysis: für Studierende der Informatik. — Springer, 2008. — С. 141—142. — ISBN 978-3-540-70854-4.
Weisstein, Eric W. Entringer Number (англ.) на сайте Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[stanley-1] Р. Стенли Перечислительная комбинаторика. — Рипол Классик. — С. 219. — ISBN 9785458261043.

[2] Stanley, Richard P. Enumerative Combinatorics (неопр.). — 2nd. — Cambridge University Press, 2011. — Т. I.

[3] Philippe Flajolet, Robert Sedgewick (2009), Analytic Combinatorics, Cambridge University Press, с. 2

[4] Folkmar Bornemann. Konkrete Analysis: für Studierende der Informatik. — Springer, 2008. — С. 141—142. — ISBN 978-3-540-70854-4.

[5] Weisstein, Eric W. Entringer Number (англ.) на сайте Wolfram MathWorld.