Цикловая раскраска

Циркулярный полный граф
Циркулярный полный граф
Вершин	n
Рёбер
Обхват
Хроматическое число	⌈n/k⌉
Свойства	(n − 2k + 1)- регулярный; Вершинно-транзитивный; Циркулянтный; Гамильтонов

Цикловую раскраску можно рассматривать как уточнение обычной раскраски графов. Цикловое хроматичеcкое число графа $G$ с обозначением $\chi _{c}(G)$ можно определить следующими эквивалентными (для конечных графов) способами.

$\chi _{c}(G)$ равен инфимуму по всем вещественным числам $r$ таким, что существует отображение из $V(G)$ в окружность с длиной, равной 1, при этом две смежные вершины отображаются в точки на расстоянии $\geqslant {\tfrac {1}{r}}$ вдоль окружности.
$\chi _{c}(G)$ равен инфимуму по рациональным числам ${\tfrac {n}{k}}$ таким, что существует отображение из $V(G)$ в циклическую группу ${\mathbb {Z} }/n{\mathbb {Z} }$ со свойством, что смежные вершины отображаются в элементы на расстоянии $\geqslant k$ друг от друга.
В ориентированном графе определим дисбаланс цикла $C$ , как значение $|E(C)|$ , делённое на меньшее из числа рёбер, направленных по часовой стрелке и числа рёбер, направленных против часовой стрелки. Определим дисбаланс ориентированного графа, как максимальный дисбаланс по всем циклам. Теперь, $\chi _{c}(G)$ равен минимальному дисбалансу по всем ориентациям графа $G$ .

Хроматическое число снарка «Цветок» J₅ равно 3, но цикловое хроматичеcкое число равно

\leqslant {\tfrac {5}{2}}

.

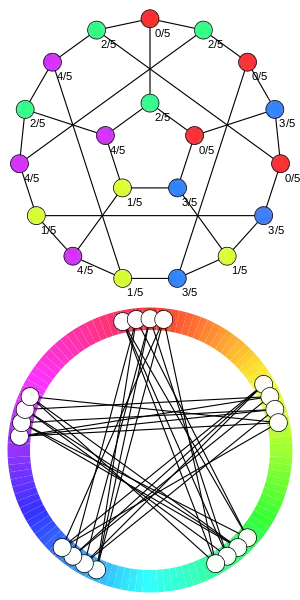
Относительно несложно видеть, что $\chi _{c}(G)\leqslant \chi (G)$ (используя определение 1 или 2), но, фактически, $\lceil \chi _{c}(G)\rceil =\chi (G)$ . В этом смысле мы говорим, что цикловое хроматичеcкое число уточняет обычное хроматическое число.

Цикловую раскраску первоначально определил Винс[1], который назвал её «звёздной раскраской».

Цикловая раскраска двойственна субъекту нигде не нулевого потока и более того, цикловая раскраска имеет естественное двойственное понятие «циркуляционный поток».

Цикловые полные графы

Для целых $n,k$ таких, что $n\geqslant 2k$ , цикловой полный граф $K_{\tfrac {n}{k}}$ (известный также как цикловая клика) — это граф с множеством вершин ${\mathbb {Z} }/n{\mathbb {Z} }$ и рёбрами между элементами на расстоянии $\geqslant k$ друг от друга. То есть, вершинами являются числа ${0,1,...,''n''-1}$ и вершина i смежна с:

i+k,i+k+1,\dots ,i+n-k\mod n

.

Например, $K_{\tfrac {n}{1}}$ является просто полным графом K_n, в то время как граф $K_{\tfrac {2n+1}{n}}$ изоморфен графу-циклу $C_{2n+1}$ .

В таком случае цикловая раскраска, согласно второму определению выше, является гомоморфизмом в цикловой полный граф. Критическое обстоятельство об этих графах заключается в том, что $K_{\tfrac {a}{b}}$ допускает гомоморфизм в $K_{\tfrac {c}{d}}$ тогда и только тогда, когда ${\tfrac {a}{b}}\leqslant {\tfrac {c}{d}}$ . Это объясняет обозначение, поскольку если рациональные числа ${\tfrac {a}{b}}$ и ${\tfrac {c}{d}}$ равны, то $K_{\tfrac {a}{b}}$ и $K_{\tfrac {c}{d}}$ гомоморфно эквивалентны. Более того, порядок гомоморфизма уточняет порядок, задаваемый полными графами в плотный порядок и соответствует рациональным числам $\geqslant 2$ . Например

K_{\tfrac {2}{1}}\to K_{\tfrac {5}{2}}\to K_{\tfrac {7}{3}}\to \dots \to K_{\tfrac {3}{1}}\to K_{\tfrac {4}{1}}\to \dots

Или, эквивалентно

K_{2}\to C_{5}\to C_{7}\to \dots \to K_{3}\to K_{4}\to \dots

Пример на рисунке можно интерпретировать, как гомоморфизм из снарка «Цветок» $J_{5}$ в $K_{\tfrac {5}{2}}\approx C_{5}$ , который идёт раньше $K_{3}$ , что соответствует факту, что $\chi _{c}(J_{5})\leqslant 2,5<3$ .

См. также

Циклический ранг

Примечания

Vince, 1988.

Литература

Adam Nadolski. Circular coloring of graphs // Graph colorings. — Providence, RI: Amer. Math. Soc., 2004. — Т. 352. — С. 123–137. — (Contemp. Math.). — doi:10.1090/conm/352/09.
Vince A. Star chromatic number // Journal of Graph Theory. — 1988. — Т. 12, вып. 4. — С. 551–559. — doi:10.1002/jgt.3190120411.
Zhu X. Circular chromatic number, a survey // Discrete Mathematics. — 2001. — Т. 229, вып. 1-3. — С. 371–410. — doi:10.1016/S0012-365X(00)00217-X.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_0e2e98039d1e9908-1] Vince, 1988.