Цепь Чуа

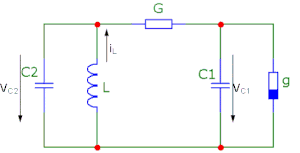
Систему уравнений для цепи изображённой на рисунке 1 можно получить используя первое правило Кирхгофа и формулу для напряжения на катушке индуктивности:

${\displaystyle \left\{{\begin{aligned}C_{1}{\frac {dv_{C_{1}}}{dt}}&=G(v_{C_{2}}-v_{C_{1}})-g(v_{C_{1}}),\\C_{2}{\frac {dv_{C_{2}}}{dt}}&=G(v_{C_{1}}-v_{C_{2}})+i_{L},\\L{\frac {di_{L}}{dt}}&=-v_{C_{2}},\end{aligned}}\right.}$

где ${\displaystyle v_{C_{1}}}$ и ${\displaystyle v_{C_{2}}}$ — напряжения на ёмкостях, ${\displaystyle i_{L}}$ — ток через катушку идуктивности, ${\displaystyle g(v_{C_{1}})}$ — кусочно-линейная функция характеризующая диод Чуа, определенная как

${\displaystyle g(v_{C_{1}})=G_{b}v_{C_{1}}+{\frac {1}{2}}(G_{a}-G_{b}){\big (}|v_{C_{1}}+E|-|v_{C_{1}}-E|{\big )}.}$

Рисунок 2. Вольт-амперная характеристика диода Чуа. Также показана нагрузочная прямая, от пересечения с которой образуются три точки равновесия d, 0 и −d

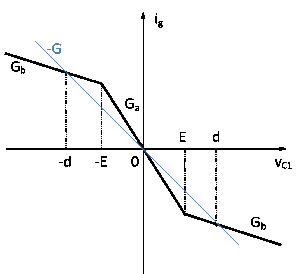
Эта нелинейная функция представлена графически на рисунке 2: крутизна внутреннего и внешнего участков есть G_a и G_b соответственно; при этом точки ±Е соответствуют изломам на графике.

Выполним следующие замены на безразмерные коэффициенты:

${\displaystyle m_{0}={\frac {G_{a}}{G}},\quad m_{1}={\frac {G_{b}}{G}},\quad \alpha ={\frac {C_{2}}{C_{1}}},\quad \beta ={\frac {C_{2}}{LG^{2}}},}$

${\displaystyle \tau ={\frac {tG}{C_{2}}},\quad x={\frac {v_{C_{1}}}{E}},\quad y={\frac {v_{C_{2}}}{E}},\quad z={\frac {i_{L}}{EG}}.}$

Основная система уравнений запишется в виде

${\displaystyle \left\{{\begin{aligned}{\frac {dx}{d\tau }}&=\alpha {\big (}y-x-h(x){\big )},\\{\frac {dy}{d\tau }}&=x-y+z,\\{\frac {dz}{d\tau }}&=-\beta y,\end{aligned}}\right.}$

где

${\displaystyle h(x)=m_{1}x+{\frac {1}{2}}(m_{0}-m_{1}){\big (}|x+1|-|x-1|{\big )}.}$

Цепь Чуа обнаруживает хаотические режимы колебаний в довольно узкой области параметров. Основные режимы колебаний условно показаны на рисунке 3.

Рисунок 3. Бифуркационная диаграмма режимов при m₀ = −8/7, m₁ = −5/7

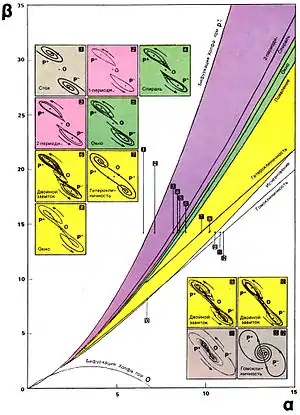
В случае, когда параметры α и β принадлежат области, обозначенной на диаграмме цифрой 1, в системе существуют два устойчивых положения равновесия d и −d и одно неустойчивое, находящееся в начале координат 0. В этом случае цепь Чуа в зависимости от начальных условий будет стремиться к одному из двух устойчивых положений равновесия. В случае, когда параметры системы находятся в области помеченной цифрой 2, в окрестности точки равновесия d или −d существует устойчивый предельный цикл. По мере приближения к границе с хаотическим режимом система претерпевает цикл удвоений периода вплоть до образования хаотического аттрактора Рёсслера. Приращение значений параметра перед наступлением каждой последующей бифуркации удвоения периода уменьшается согласно соотношению Фейгенбаума. При попадании параметров в область, помеченную цифрой 6, образуется странный аттрактор (рисунок 4), называемый «двойной завиток» (англ. double scroll). При этом типе поведения траектория система проходит в окрестности и верхнего, и нижнего положения равновесия. Внутри области существования аттрактора «двойной завиток» также существуют окна периодичности, подобные тем, которые существовали в области аттрактора Рёсслера. Отличием их является то, что периодическая орбита в этом случае охватывает оба положения равновесия. Когда параметры α и β переходят в область, помеченную на рисунке 3 цифрой 11, в колебательной системе наблюдаются колебания неограниченно нарастающей амплитуды вне зависимости от начальных условий. Поскольку диод Чуа реализуется на операционных усилителях, он имеет ограниченный динамический диапазон, и поэтому в системе существует также большой по размерам устойчивый предельный цикл, охватывающий все сегменты характеристики диода Чуа.

На рисунках 5, 6 показаны временные зависимости колебаний, обнаруживаемых данной системой.

• 
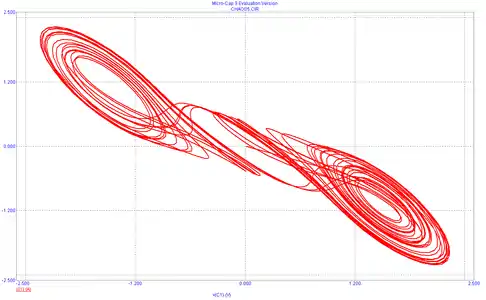  Рисунок 4. Аттрактор типа двойной завиток. Фигура Лиссажу i_L от v_С1 при L = 1/7 Гн; G = 0,7 См; C1 = 1/9 Ф; C2 = 1Ф; G_a = −0,8 А/В; G_b = −0,5 А/В
• 
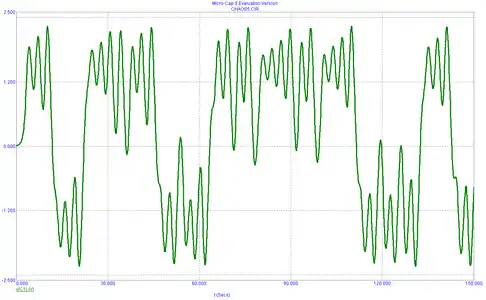  Рисунок 5. Временная зависимость v_C1 для случая L = 1/7 Гн; G = 0,7 См; C1 = 1/9Ф; C2 = 1Ф; G_a = −0,8 А/В; G_b = −0,5 А/В
• 
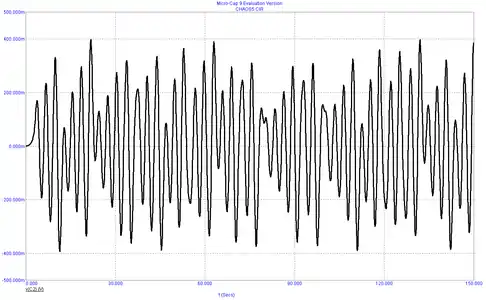  Рисунок 6. Временная зависимость v_C2 для случая L = 1/7 Гн; G = 0,7 См; C1 = 1/9 Ф; C2 = 1 Ф; G_a = −0,8 А/В; G_b = −0,5 А/В

Термин «Осциллятор Чуа» используется для рассмотрения цепи Чуа с учётом активного сопротивления катушки индуктивности L. Данная схема имеет ещё большее число разнообразных режимов и может быть реализована практически (рисунок 7).

Рисунок 7. Практическая схема осциллятора Чуа. L1 = 8,5 мГн, C1 = 4,8 нФ, C2 = 69 нФ, R = 1,3 кОм

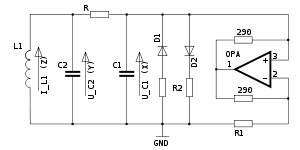
Принимая R₀ — активное сопротивление катушки индуктивности L, получим систему уравнений

${\displaystyle \left\{{\begin{aligned}C_{1}{\frac {dv_{c_{1}}}{dt}}&=G(v_{C_{2}}-v_{C_{1}})-g(v_{C_{1}}),\\C_{2}{\frac {dv_{c_{2}}}{dt}}&=G(v_{C_{1}}-v_{C_{2}})+i_{L},\\L{\frac {di_{L}}{dt}}&=-v_{C_{2}}+R_{0}i_{L}.\end{aligned}}\right.}$

Лёгкость практической реализации, а также наличие относительно простой математической модели делает цепь Чуа удобной моделью для изучения хаоса.

Мемристор

• Кузнецов А. П. Наглядные образы хаоса // Соросовский образовательный журнал, 2000, № 11, с. 104—110;
• Бугаевский М. Ю., Пономаренко В. И. Исследование поведения цепи Чуа. Учебно-методическое пособие, — Саратов: Издательство ГосУНЦ «Колледж», 1998. — 29 с.
• Matsumoto, T. A Chaotic Attractor from Chua’s Circuit, IEEE Transactions on Circuits & Systems,1984, vol. CAS-31, no. 12, pp. 1055–1058.
• Chua, L. O., Komuro, M., Matsumoto, T. "The Double Scroll Family", IEEE Transactions on Circuits & Systems, 1986, vol. CAS-33, no. 11, pp. 1073–1118.
• T. Matsumoto, L. O. Chua, M. Komuro. «Birth and death of the double scroll», Physica D Volume 24 , Issue 1-3 (Jan/Feb 1987).
• Stankevich N. V.; Kuznetsov N. V.; Leonov G. A.; Chua L. (2017). "Scenario of the birth of hidden attractors in the Chua circuit". International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. 27 (12): 1730038–188 https://doi.org/10.1142/S0218127417300385
• Н. В. Кузнецов. Теория скрытых колебаний и устойчивость систем управления // Известия РАН. Теория и Системы управления. — 2020. — № 5. — С. 5—27. — doi:10.31857/S0002338820050091.

• Chua’s Circuit diagrams, equations, simulation and pictures Чуа Схемы, формулы, моделирования и фотографии
• Chua’s Circuit: Diagram and discussion
• NOEL laboratory. Leon O. Chua’s laboratory at the University of California, Berkeley
• References
• ТИИЭР Том 75 № 8 Август 1987