Флексагон

Флексагоны (от англ. to flex, лат. flectere — складываться, сгибаться, гнуться и греч. ωνος — угольник) — плоские модели из полосок бумаги, способные складываться и сгибаться определённым образом. При складывании флексагона становятся видны поверхности, которые ранее были скрыты в конструкции флексагона, а прежде видимые поверхности уходят внутрь.

Флексагон в процессе разворачивания.

Многие флексагоны имеют квадратную (тетрафлексагоны) или шестиугольную (гексафлексагоны) форму. Впрочем, существуют флексагоны других форм, включая прямоугольные и кольцевые.

Для различения плоскостей на секторы флексагона наносят цифры, буквы, элементы изображения или просто окрашивают в определённый цвет.

История

Первый флексагон был открыт в 1939 году английским студентом Артуром Стоуном, изучавшим тогда математику в Принстонском университете в США. Бумага формата Letter была слишком широкой и не умещалась в скоросшиватель, предназначенный для бумаги формата A4. Стоун обрезал края бумаги и из получившихся полосок стал складывать различные фигуры, одна из которых оказалась тригексафлексагоном[1][2].

Вскоре был создан «Флексагонный комитет», в который вошли, кроме Стоуна, аспирант-математик Бриан Таккерман, аспирант-физик Ричард Фейнман и преподаватель математики Джон У. Тьюки[2].

К 1940 году Фейнман и Тьюки разработали теорию флексагонов, заложив тем самым основания для всех последующих исследований. Теория не была опубликована полностью, хотя отдельные её части впоследствии были открыты заново[2]. Нападение на Пёрл-Харбор приостановило работу «Флексагонного комитета», а война вскоре разбросала всех четырёх его учредителей в разные стороны[3].

Популярность флексагоны получили после появления в декабрьском номере журнала «Scientific American» за 1956 год первой колонки Мартина Гарднера «Mathematical Games», посвящённой гексафлексагонам[4][5].

Флексагоны неоднократно были запатентованы в виде игрушек, но не получили широкого коммерческого распространения[6][7].

Виды флексагонов

Поверхности флексагона могут состоять из равносторонних или равнобедренных треугольников, квадратов, пятиугольников и т. д. Флексагон может допускать появление определённого числа поверхностей; некоторые из них могут быть аномальными (т. е. включающими в себя секторы с разными цифрами). Флексагон заданной формы с заданным количеством плоскостей может быть изготовлен из разных развёрток. Более того, даже одна и та же развёртка может допускать разные варианты сворачивания[3][8].

Наименования флексагонов

Названия многих флексагонов образованы по принципу «приставка (число поверхностей) + приставка (форма) + „флексагон“». Таким образом, первая приставка обозначает, сколько у флексагона поверхностей, которые могут рано или поздно раскрыться, а вторая — на сколько частей разделена каждая такая поверхность. Например, тетратетрафлексагон — это флексагон с четырьмя поверхностями, каждая из которых состоит из четырёх квадратов; гексагексафлексагон — флексагон с шестью поверхностями, каждая из которых состоит из шести треугольников; додекагексафлексагон — флексагон с двенадцатью («додека») поверхностями, каждая из которых состоит из шести («гекса») секторов, и т. д.[9]

Впрочем, общепринятой системы наименований для флексагонов нет. Мартин Гарднер использовал термины «тетрафлексагон» и «гексафлексагон» для обозначения флексагонов, состоящих из квадратов и треугольников соответственно, причём поверхности тетрафлексагона могли состоять из четырёх или шести квадратов[3]. В книге Flexagons Inside Out флексагоны обозначаются по форме секторов (квадратный, пятиугольный и т. п.)[10][11]

В более позднее время окта- и додекафлексагонами стали называть флексагоны с 8 и 12 треугольными секторами соответственно[8]. Если секторы поверхностей флексагона представляют собой правильные или равнобедренные треугольники, то помимо гексафлексагонов существуют треугольные тетра-, пента-, гепта-, октафлексагоны[11].

В журналах «Наука и жизнь» использовалась в основном система приставок ИЮПАК[12][13][14][15].

Гексафлексагоны
Гексафлексагоны

Гексафлексагон — это флексагон, имеющий форму правильного шестиугольника. Каждая поверхность флексагона состоит из шести треугольных секторов.

Существует множество гексафлексагонов, различающихся по числу поверхностей. Известны гексафлексагоны с тремя, четырьмя, пятью, шестью, семью, девятью, двенадцатью, пятнадцатью, сорока восемью поверхностями; количество плоскостей ограничено лишь тем, что бумага имеет ненулевую толщину[9][1][3][16][17].

Число видов гексафлексагонов быстро растёт с увеличением числа его поверхностей: существуют 3 вида гексагексафлексагона, 4 вида гептагексафлексагона, 12 видов октагексафлексагонов, 27 видов эннагексафлексагонов и 82 вида декагексафлексагона[3][18].

Тригексафлексагон

Соответственно названию, тригексафлексагон — это шестиугольный флексагон с тремя поверхностями. Это самый простой из всех гексафлексагонов (не считая унагексафлексагона и дуогексафлексагона). Он представляет из себя сплющенную ленту Мёбиуса[1][3]. Тригексафлексагон можно свернуть из полоски бумаги, разделённой на десять равносторонних треугольников[16][1]. Складывание тригексафлексагона осуществляется методом[16][1][19], носящим название pinch flex[20], с поворотом на 60° после каждого складывания.

Гексагексафлексагон

Гексагексафлексагон — флексагон с шестью шестиугольными поверхностями. Гексагексафлексагон можно изготовить из полоски длиной в 19 треугольников[9][19][17].

Тетрафлексагоны

Простейший тетрафлексагон (флексагон с квадратными поверхностями) — тритетрафлексагон, имеющий три поверхности. В любой момент видимыми являются лишь две из трёх поверхностей.

Более сложные гексатетрафлексагон и декатетрафлексагон собираются из крестообразной развёртки без использования клея[12]. Тетрафлексагоны с числом плоскостей 4n + 2 также можно изготавливать из квадратных рамок[3].

Из зигзагообразных полосок бумаги можно изготовить тетратетрафлексагон и другие тетрафлексагоны с числом плоскостей, кратным 4[21].

Кольцевые флексагоны

Кольцевой флексагон — флексагон, поверхность которого представляет собой «кольцо» из многоугольников. Для наименования кольцевых флексагонов может быть использована приставка «цирко», например, пентациркодекафлексагон — кольцевой флексагон с пятью плоскостями, состоящими из десяти многоугольников (пятиугольников) каждая[22]; тригемициркогексафлексагон — флексагон с тремя поверхностями, каждая из которых представляет собой кольцо (цирко) из половинок (геми) правильных шестиугольников (гекса)[14].

Путь Таккермана
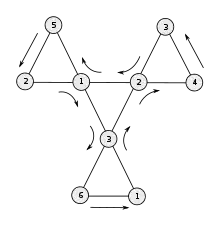
Диаграмма пути Таккермана для гексагексафлексагона

Простой способ обнаружить все поверхности гексафлексагона — обход Таккермана — заключается в том, чтобы держать флексагон за один угол и раскрывать модель до тех пор, пока она не перестанет раскрываться, затем повернуть флексагон на 60° по часовой стрелке, взяться за соседний угол и повторить то же самое[19][17].

При обходе Таккермана плоскости гексагексафлексагона будут раскрываться в порядке: 1,2,5,1,2,3,4,2,3,1,6,3 (или в обратном порядке), после чего последовательность повторится. Эту последовательность называют путём Таккермана[19][17].

Методы складывания («флексы»)

Гексафлексагоны

Описанный выше метод складывания гексафлексагона, используемый для обхода всех плоскостей (пути Таккермана), носит название pinch flex[20]. Существуют следующие методы складывания гексафлексагонов:

  • pinch flex[20] (выполним на гексафлексагонах с тремя и более плоскостями)
  • v-flex[23][24] (выполним на гексафлексагонах с четырьмя и более плоскостями)
  • tuck flex[25], «лодочка-гексаэдр»[19] (выполним на гексафлексагонах с четырьмя плоскостями и более)

и др.[26]

Аномалии

Плоскость флексагона (совокупность секторов), на которой присутствуют разные цифры, называется аномальной плоскостью, а флексагон с видимой аномальной плоскостью (в аномальном положении) — аномальным флексагоном[19][17][27]. Появление аномальных плоскостей возможно на флексагонах достаточно высокого порядка, например, на гексагексафлексагоне[19], додекагексафлексагоне[27]. Простейшим гексафлексагоном, допускающим появление аномалий, является тетрагексафлексагон[22]. Для достижения аномальных плоскостей используются методы складывания, отличные от «стандартного» pinch flex[19].

См. также

Примечания
  1. Наука и жизнь, 1970, №1
  2. Antony S. Conrad, Daniel K. Hartline The story of the Flexagon
  3. Мартин Гарднер, Математические головоломки и развлечения
  4. Martin Gardner's Collections of "Mathematical Games" Columns. Muppetlabs
  5. Gardner, Martin. Flexagons (англ.) // Scientific American. — Springer Nature, 1956. — December (vol. 195, no. 6). — P. 162—168. — doi:10.1038/scientificamerican1256-162.
  6. Rogers, Russell E.; Andrea, Leonard D. L. Changeable amusement devices and the like. Freepatentsonline.com (21 апреля 1959). Дата обращения: 30 июля 2013. Архивировано 13 августа 2013 года.
  7. Patents
  8. Scott Sherman. Flexagon Naming and Terminology. Архивировано 5 января 2009 года.
  9. Наука и жизнь, 1970, №3
  10. Les Pook, Flexagons Inside Out
  11. Scott Sherman. Triangle Flexagon Bestiary. Архивировано 12 июня 2008 года.
  12. Наука и жизнь, 1975, №9
  13. Наука и жизнь, 1992, №4
  14. Наука и жизнь, 1993, №11
  15. Наука и жизнь, 1993, №12
  16. Flexagons. Mathematische Basteleien. Архивировано 9 марта 2017 года.
  17. Наука и жизнь, 1970, №2
  18. последовательность A000207 в OEIS The number of hexaflexagons of order n+2
  19. Наука и жизнь, 1977, №2
  20. Scott Sherman. The Pinch Flex. Архивировано 5 января 2009 года.
  21. Наука и жизнь, 1972, №3
  22. Наука и жизнь, 1977, №8
  23. Flexagon Portal v-flex video
  24. Scott Sherman. The V flex. Архивировано 23 августа 2016 года.
  25. Scott Sherman. The Tuck Flex. Архивировано 23 августа 2016 года.
  26. Scott Sherman. Triangle Flexagon Flexes. Архивировано 23 августа 2016 года.
  27. Квант, 1992, №10

Литература

Книги

Статьи
  • А. А. Панов. Флексагоны, флексоры, флексманы // Квант. — 1988. — № 7. — С. 10—14.
  • И. Кан. Аномальные флексагоны // Квант. — 1992. — № 10. — С. 57—59.
  • Флексагоны // Наука и жизнь. — 1970. — № 1. — С. 124—125. Тригексафлексагон
  • Флексагоны // Наука и жизнь. — 1970. — № 2. — С. 68—69. Гексагексафлексагон, путь Таккермана
  • Флексагоны // Наука и жизнь. — 1970. — № 3. — С. 154—155. Другие гексафлексагоны
  • Флексагоны // Наука и жизнь. — 1970. — № 8. — С. 149. Переписка с читателями
  • Флексагоны // Наука и жизнь. — 1972. — № 3. — С. 142—143. Тетрафлексагоны
  • Флексагоны // Наука и жизнь. — 1972. — № 4. — С. 107. Флексотрубка Стоуна
  • Флексагоны // Наука и жизнь. — 1975. — № 7. — С. 154—155. Флексотрубка Стоуна (продолжение)
  • Флексагоны // Наука и жизнь. — 1975. — № 9. — С. 121—123. Гексатетрафлексагон, декатетрафлексагон, приставки IUPAC
  • И. Константинов. Флексагонными тропами // Наука и жизнь. — 1977. — № 2. — С. 92—96, V. Туннельный перевод
  • Флексагоны // Наука и жизнь. — 1977. — № 8. — С. 98—99. Пространственные модели диаграмм перевода. Пентациркодекафлексагон
  • И. Кан. Гемитетрафлексагоны // Наука и жизнь. — 1992. — № 4. — С. 126—127. Гемитетрафлексагоны
  • И. Кан. Гемитетра- и гемигексафлексагоны // Наука и жизнь. — 1993. — № 11. — С. 150—152.
  • И. Кан. Треугольные флексагоны // Наука и жизнь. — 1993. — № 12. — С. 42—43.

Ссылки
  • Harold V. McIntosh, Antony S. Conrad, Daniel K. Hartline. Flexagons (англ.) (1962,2000,2003). — Статьи по флексагонам в формате PDF. Дата обращения: 30 июля 2013. Архивировано 13 августа 2013 года.
  • Harold V. McIntosh. My Flexagon Experiences (англ.). — Contains valuable historical information and theory; the author's site has several flexagon related papers listed in . Дата обращения: 30 июля 2013. Архивировано 13 августа 2013 года.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.