Уравнение Баркера

Решение задачи двух тел дает уравнение траектории в полярных координатах в виде

${\displaystyle r={\frac {p}{1+e\,\cos \vartheta }}}$

где ${\displaystyle p}$ — параметр орбиты; ${\displaystyle e}$ — эксцентриситет орбиты; ${\displaystyle \vartheta }$ — истинная аномалия — угол между радиус-вектором текущего положения тела и направлением на перицентр. С другой стороны, справедлив второй закон Кеплера

${\displaystyle r^{2}\,{\frac {d\vartheta }{dt}}=c}$

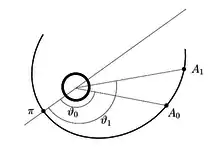
где ${\displaystyle c}$ — константа площадей. Исходя из этих уравнений легко получить интеграл, связывающий время и истинную аномалию в точках ${\displaystyle A_{0}}$ и ${\displaystyle A_{1}}$ орбиты.

${\displaystyle t_{1}-t_{0}={\frac {p^{2}}{c}}\,\int \limits _{\vartheta _{0}}^{\vartheta _{1}}{\frac {d\vartheta }{\left(1+e\,\cos \vartheta \right)^{2}}}}$

К выводу уравнения Кеплера и уравнения Баркера

Способ вычисления данного интеграла зависит от величины эксцентриситета (см. Уравнение Кеплера). Для параболической траектории ${\displaystyle e=1}$, в этом случае приходим к тривиальной цепочке преобразований

${\displaystyle t_{1}-t_{0}={\frac {p^{2}}{c}}\,\int \limits _{\vartheta _{0}}^{\vartheta _{1}}{\frac {d\vartheta }{\left(1+\cos \vartheta \right)^{2}}}={\frac {p^{2}}{4\,c}}\,\int \limits _{\vartheta _{0}}^{\vartheta _{1}}\left(1+{\rm {tg}}^{2}{\frac {\vartheta }{2}}\right)^{2}\,d\vartheta =\left|{\rm {tg}}{\frac {\vartheta }{2}}=z,\,d\vartheta ={\frac {2\,dz}{1+z^{2}}}\right|={\frac {p^{2}}{2\,c}}\int \limits _{{\rm {tg}}{\frac {\vartheta _{0}}{2}}}^{{\rm {tg}}{\frac {\vartheta _{1}}{2}}}\left(1+z^{2}\right)\,dz={\frac {p^{2}}{2\,c}}\left[{\rm {tg}}{\frac {\vartheta _{1}}{2}}-{\rm {tg}}{\frac {\vartheta _{0}}{2}}+{\frac {1}{3}}\left({\rm {tg}}^{3}{\frac {\vartheta _{1}}{2}}-{\rm {tg}}^{3}{\frac {\vartheta _{0}}{2}}\right)\right]}$

Учитывая, что параметр орбиты связан с константой площадей

${\displaystyle p={\frac {c^{2}}{\mu }}}$

где ${\displaystyle \mu }$ — гравитационный параметр центрального тела, а константа площадей, в случае параболического движения

${\displaystyle c=r_{\pi }\,v_{\pi }=r_{\pi }\,{\sqrt {\frac {2\,\mu }{r_{\pi }}}}}$

где ${\displaystyle r_{\pi }}$ — расстояние до перицентра; ${\displaystyle v_{\pi }}$ — скорость в перицентре, при движении по параболе являющаяся параболической скоростью. Тогда, получаем для параметра орбиты ${\displaystyle p=2\,r_{\pi }}$ и приходим к окончательному выражению

${\displaystyle t_{1}-t_{0}=r_{\pi }{\sqrt {\frac {2\,r_{\pi }}{\mu }}}\left[{\rm {tg}}{\frac {\vartheta _{1}}{2}}-{\rm {tg}}{\frac {\vartheta _{0}}{2}}+{\frac {1}{3}}\left({\rm {tg}}^{3}{\frac {\vartheta _{1}}{2}}-{\rm {tg}}^{3}{\frac {\vartheta _{0}}{2}}\right)\right]}$

Теперь примем, что начальная точка траектории — перицентр, значит ${\displaystyle \vartheta _{0}=0}$ и преобразуем полученную зависимость к виду

${\displaystyle n\,\left(t-t_{0}\right)={\rm {tg}}{\frac {\vartheta }{2}}+{\frac {1}{3}}{\rm {tg}}^{3}{\frac {\vartheta }{2}}}$

где ${\displaystyle n={\sqrt {\frac {\mu }{2\,r_{\pi }^{3}}}}}$ — среднее движение небесного тела. В итоге, получаем кубическое уравнение вида

${\displaystyle S+{\frac {1}{3}}\,S^{3}-M=0}$

где ${\displaystyle S={\rm {tg}}{\frac {\vartheta }{2}}}$, ${\displaystyle M=n\,\left(t-t_{0}\right)}$ — средняя аномалия орбиты небесного тела. Данное уравнение называют уравнением Баркера.

Это уравнение представляет собой неявную зависимость истинной аномалии от времени ${\displaystyle \vartheta (t)}$ при движении небесного тела по параболической траектории.

Уравнение

${\displaystyle S+{\frac {S^{3}}{3}}-M=0}$

является кубическим уравнением, записанным в канонической форме Кардано и имеет аналитическое решение. Средствами компьютерной алгебры легко получить это решение, содержащее один действительный и два комплексно-сопряженных корня

${\displaystyle S_{1}=x-{\frac {1}{x}},\quad S_{2,3}=-{\frac {x}{2}}+{\frac {1}{2\,x}}\pm i\,{\frac {\sqrt {3}}{2}}\,\left(x+{\frac {1}{x}}\right)}$

где ${\displaystyle x={\frac {1}{2}}\,{\sqrt[{3}]{12\,M+4\,{\sqrt {9\,M^{2}+4}}}}}$

Физическому смыслу данной задачи соответствует только действительный корень, поэтому можно записать

${\displaystyle S={\rm {tg}}{\frac {\vartheta }{2}}=x-{\frac {1}{x}}}$

Имея этот корень, можно вычислить синус и косинус истинной аномалии

${\displaystyle \cos \vartheta ={\frac {1-S^{2}}{1+S^{2}}},\quad \sin \vartheta ={\frac {2\,S}{1+S^{2}}}\quad }$

по которым, с учетом их знака, определяется истинная аномалия ${\displaystyle \vartheta \in [0,\,2\,\pi )}$

• Уравнение Кеплера
• Законы Кеплера
• Задача двух тел

1. С. Херрик. Астродинамика. Том 1. — М.: Мир, 1976. — С. 318.
2. А. Рой. Движение по орбитам. — М.: Мир, 1981. — С. 544.