Универсальное множество точек

Рисунок графа вложенных треугольников на решётке. В любом рисунке этого графа по меньшей мере половина треугольников должна иметь образовывать вложенную цепочку, так что потребуется ограничивающий прямоугольник размером по меньшей мере n/3 × n/3. Показанное на рисунке представление графа имеет близкое к этому значение n/3 × n/2

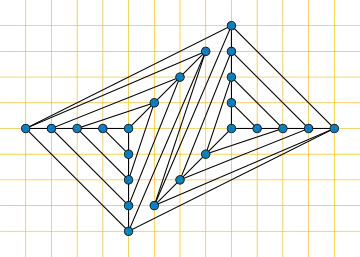
Если n не превосходит десяти, существует универсальное множество точек, имеющее в точности n точек, но для всех n ≥ 15 требуются дополнительные точки [1].

Некоторые авторы показали, что подмножество целочисленной решётки размера O(n) × O(n) является универсальным. В частности, Фрейсикс, Пах и Поллак[2] показали, что решётка (2n − 3) × (n − 1) является универсальной, а Шнайдер[3] уменьшил до треугольного подмножества решётки (n − 1) × (n − 1) с n²/2 − O(n) точками. Модифицируя метод Фрейсикса, Паха и Шнайдера, Бранденбург[4] нашёл вложение любого планарного графа в треугольное подмножество решётки, содержащей 4n²/9 точек. Универсальное множество точек в виде прямоугольной решётки должно иметь размер по меньшей мере n/3 × n/3 [5], но это не исключает возможность существования меньшего универсального множества точек других типов. Наименьшие известные универсальные множества точек не основаны на решётках, а строятся из суперсхем (перестановок, содержащих все образы перестановок заданного размера). Универсальные множества точек, построенные таким образом, имеют размер n²/4 − O(n)[6].

Фрейсикс, Пах и Поллак[2] доказали первую нетривиальную нижнюю границу размера универсального множества точек в виде n + Ω(√n), а Хробак и Карлофф[7] показали, что универсальное множество точек должно содержать по меньшей мере 1.098n − o(n) точек. Куровски[8] предложил даже более сильную границу 1.235n − o(n), которая остаётся лучшей нижней границей [9].

Закрытие промежутка между известными линейными границами и квадратичными верхними границами остаётся открытой проблемой[10].

Подклассы планарных графов могут, в общем случае, иметь меньшие универсальные множества (множества точек, которые позволяют рисование всех графов с n вершинами с прямыми рёбрами в подклассе), чем полный класс всех планарных графов, и во многих случаях существуют универсальные множества точек, имеющие в точности n точек. Например, несложно видеть, что любое множество из n точек в выпуклой позиции (которые служат вершинами выпуклого многоугольника), является универсальным для n вершинных внешнепланарных графов, и, в частности, для деревьев. Менее очевидно, что любое множество из n точек в общем положении (никакие три не лежат на одной прямой) остаётся универсальным для внешнепланарных графов[11].

Планарные графы, которые могут быть разбиты на вложенные циклы, и планарные графы с ограниченной путевой шириной имеют универсальное множество точек почти линейного размера[12][6]. Планарные 3-деревья имеют универсальные множества точек размера O(n^5/3). Та же самая граница имеет место для параллельно-последовательных графов[13].

Дугова диаграмма

Как и в случае рисования графов с прямыми рёбрами, универсальные множества точек изучались для других стилей. В большинстве этих случаев существуют универсальные множества точек, имеющие в точности n точек, и основываются они на топологическом книжном вложении, в котором вершины располагаются на прямой на плоскости, а рёбра рисуются как кривые, которые пересекают эту линию максимум один раз. Например, любое множество n коллинеарных точек является универсальным для дуговой диаграммы, в которой каждое ребро представлено либо как одна полуокружность, либо как гладкая кривая, образованная двумя полуокружностями[14].

Можно показать, что при использовании подобного расположения любая выпуклая кривая на плоскости содержит подмножество из n точек, которое является универсальным для рисунков в виде ломаных с максимум одним изломом на ребро[15]. Это множество содержит только вершины рисунка, но не точки излома. Известны бо́льшие множества, которые можно использовать для рисунков с помощью ломаных, в которых вершины и все точки излома являются точками множества[16].