Граф вложенных треугольников

Двуусечённая бипирамида

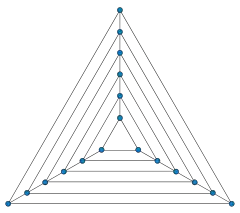
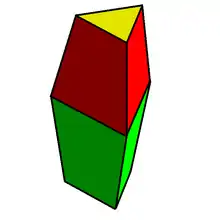
Граф вложенных треугольников с двумя треугольниками является графом треугольной призмы, а граф вложенных треугольников с тремя треугольниками — это граф двуусечённой бипирамиды. Более обще, поскольку графы встроенных треугольников планарны и вершинно 3-связны, из теоремы Штайница следует, что все они могут быть представлены как выпуклые многогранники.

Альтернативное геометрическое представление этих графов может быть задано путём склеивания треугольных призм по треугольным граням. Число вложенных треугольников на единицу больше числа склеенных призм. Однако при использовании прямоугольных призм процесс их склеивания приводит к тому, что смежные прямоугольные грани компланарны, так что в результате не получим строго выпуклое тело.

Рисунок графа вложенных треугольников на решётке. Это представление использует меньшую площадь, чем представление Фрати и Патригнани[1], но, в отличие от их представления, не обобщается до максимального планарного суперграфа графа вложенных треугольников.

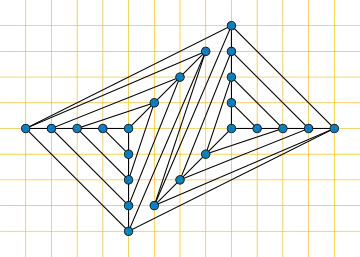
Название «граф вложенных треугольников» предложили Долев, Лейтон и Трики[2], которые использовали его, чтобы показать, что рисунок планарного графа с n вершинами на целочисленной решётке (с рёбрами в виде отрезков) может потребовать ограничивающий прямоугольник размера по меньшей мере ${\displaystyle {\tfrac {n}{3}}\times {\tfrac {n}{3}}}$[3]. В таком рисунке не имеет значения, какая грань выбрана в качестве внешнего ребра, некоторая подпоследовательность по меньшей мере в n/6 треугольников должна быть нарисована вложенными друг в друга и в этой части рисунка каждый треугольник должен использовать на две строки и на два столбца больше, чем следующий внутренний треугольник. Если выбор внешней грани не позволен как часть алгоритма рисования, но задан как часть входа, те же доводы показывают, что необходим ограничивающий прямоугольник размера ${\displaystyle {\tfrac {2n}{3}}\times {\tfrac {2n}{3}}}$ и рисунок с такими размерами существует.

Для рисунков, в которых внешняя грань может свободно выбираться, нижняя граница площади Долева, Лейтона и Трики[2] может не быть жёсткой. Фрати и Патригнани[1] показали, что этот граф и любой граф, образованный добавлением диагоналей к его четырёхугольникам, может быть нарисован в прямоугольнике размером ${\displaystyle {\tfrac {n}{3}}\times {\tfrac {2n}{3}}}$. Если никаких дополнительных диагоналей не добавлено, граф вложенных треугольников может быть нарисован даже с меньшей площадью, примерно ${\displaystyle {\tfrac {n}{3}}\times {\tfrac {n}{2}}}$ как на рисунке. Закрытие промежутка между верхней границей ${\displaystyle {\tfrac {2n^{2}}{9}}}$ и нижней границей ${\displaystyle {\tfrac {n^{2}}{9}}}$ площади максимального планарного дополнения вложенного треугольного графа остаётся открытой проблемой[4].

Нерешённые проблемы математики: Какова площадь минимального ограничивающего прямоугольника при рисовании вложенного треугольного графа на решётке или его максимального планарного пополнения?

Варианты вложенных треугольных графов использовались для многих других построениях нижних границ при рисовании графов, например по площади прямоугольного представления (когда вершины представлены прямоугольниками, а рёбра рисуются как ломаные с параллельными осям частями)[5], площади рисунков с перпендикулярными пересечениями[6] или относительной площади планарного представления по сравнению с непланарным[7].