Теория волны-пилота

Теория волны-пилота показывает, что есть теория, которая реалистична и детерминирована, и при этом она пытается предсказывать экспериментальные результаты квантовой механики, например двухщелевой эксперимент.

Теория волны-пилота основывается на динамике Гамильтона — Якоби[3], а не на лагранжевой или гамильтоновой динамике. Используя уравнения Гамильтона-Якоби

${\displaystyle H\left(\mathbf {q} ,{\partial S \over \partial \mathbf {q} },t\right)+{\partial S \over \partial t}\left(\mathbf {q} ,t\right)=0}$

— можно получить уравнение Шрёдингера.

Рассмотрим классическую частицу, положение которой неизвестно. Мы должны рассматривать её статистически, так что только плотность вероятности ρ(х, t) известна. Вероятность должна сохраняться, то есть ${\displaystyle \int \rho \,d^{3}x=1}$ для каждого t. Поэтому она должна удовлетворять уравнению непрерывности

${\displaystyle \partial \rho /\partial t=-\nabla \cdot (\rho v)\quad (1)}$

где v(x, t) есть скорость частицы.

В формулировке Гамильтона-Якоби классической механики скорость определяется выражением ${\displaystyle v(x,t)={\frac {\nabla S(x,t)}{m}}}$ , где S(x, t) является решением уравнения Гамильтона-Якоби:

${\displaystyle -{\frac {\partial S}{\partial t}}={\frac {\left(\nabla S\right)^{2}}{2m}}+{\tilde {V}}(x)\quad (2),}$

где ${\displaystyle {\tilde {V}}}$ является внешним потенциалом, в поле которого происходит движение частиц.

Мы можем объединить уравнения (1) и (2) в единую систему уравнений путём введения комплексной функции ${\displaystyle \psi ={\sqrt {\rho }}e^{\frac {iS}{\hbar }}}$. Тогда эти два уравнения эквивалентны:

${\displaystyle i\hbar {\frac {\partial \psi }{\partial t}}=\left(-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V\right)\psi \quad (3)}$,

где

${\displaystyle V={\tilde {V}}-Q}$

и

${\displaystyle \quad Q=-{\frac {\hbar ^{2}}{2m}}{\frac {\nabla ^{2}{\sqrt {\rho }}}{\sqrt {\rho }}}\quad (4)}$

Уравнение (3) совпадает со стандартным уравнением Шредингера для волновой функции ${\displaystyle \psi }$ квантовой частицы во внешнем потенциале ${\displaystyle V}$. Возвращаясь к уравнению (2), мы видим, что квантовая механика может быть записана в форме уравнений движения классической механики, если вместо обычной потенциальной энергии использовать выражение ${\displaystyle {\tilde {V}}{=}V{+}Q}$, которое включает дополнительный нелокальный квантовый потенциал ${\displaystyle Q}$, зависящий от кривизны амплитуды волновой функции.

Выявленная связь между уравнениями классической и квантовой механики лежит в основе теории Маделунга — де Бройля — Бома, известной также как гидродинамическая формулировка уравнения Шредингера. В рамках данной теории отпадает необходимость явного введения волны-пилота. Исходным пунктом теории является представление волновой функции ${\displaystyle \psi ={\sqrt {\rho }}e^{\frac {iS}{\hbar }}}$ в полярных координатах, где ${\displaystyle \rho (x)}$ предполагается неотрицательной амплитудой вероятности нахождения частицы в точке ${\displaystyle x}$, a действительная величина ${\displaystyle S}$ определяет фазу волновой функции. Подстановка этого представления в уравнение Шредингера (3) позволяет переписать уравнения эволюции в новых переменных ${\displaystyle \rho (x,t)}$ и ${\displaystyle v(x,t)={\tfrac {\nabla S(x,t)}{m}}{=}{\tfrac {\hbar }{m}}\mathrm {Im} [{\tfrac {\nabla \psi }{\psi }}]}$:

${\displaystyle {\frac {\partial {\rho (x,t)}}{\partial t}}{=}-\mathrm {div} (v\rho ),\quad }$(5а)

${\displaystyle m{\frac {du}{dt}}{=}{-}\mathrm {grad} (V{+}Q).\quad }$(5б)

Нетрудно видеть, что первое из этих уравнений совпадает с уравнением непрерывности для некоторой "квантовой жидкости", с плотностью ${\displaystyle \rho }$ и скоростью течения ${\displaystyle v}$. Второе уравнение по сути представляет собой аналог второго закона Ньютона, где снова появляется квантовый потенциал Q, заданный формулой (2).

(Нажмите, чтобы запустить анимацию) Интерференция встречных гауссовских волновых пакетов в гидродинамическом представлении Маделунга-де Бройля-Бома. В отличие от стандартной Шредингеровской картины, в которой встречные пакеты свободно проходят сквозь друг друга, интерференция в гидродинамическом описании есть результат рассеяния сталкивающихся потоков квантовой жидкости.

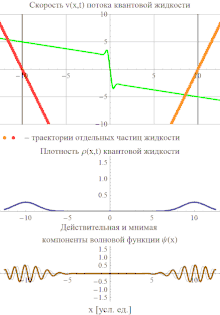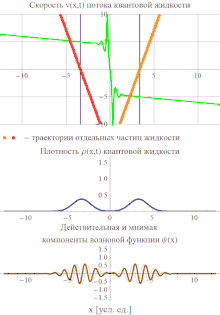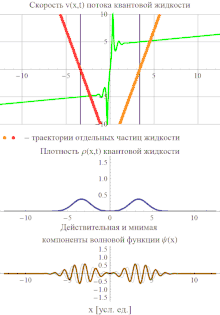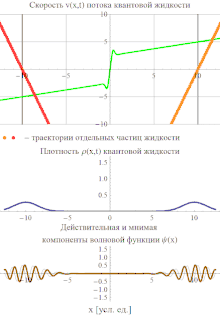
Уравнения (5) являются основными уравнениями гидродинамического описания квантовой механики. Вся их квантовость "спрятана" в потенциале Q, который задает нелокальное, неаддитивное и в существенной степени сингулярное взаимодействие между частицами квантовой жидкости. В частности, как сам квантовый потенциал, так и его градиент обычно обращаются в бесконечность в точках, где ${\displaystyle \rho (x)=0}$, благодаря чему частицы квантовой жидкости могут мгновенно набирать бесконечные скорости и проскакивать через "сухие" места, где ${\displaystyle \rho (x)}$ обращается в нуль. Из-за этого динамика, определяемая уравнениями (5), обладает качественными отличиями от классической. В качестве наглядного примера интересно рассмотреть формирование интерференционной картины двумя свободно распространяющимися навстречу друг другу гауссовскими волновыми пакетами. Напомним, что в стандартной интерпретации квантовой механики интерференционная картина возникает благодаря принципу квантовой суперпозиции, позволяющему волновым функциям пакетов проходить сквозь друг друга, не взаимодействуя. В то же время, потоки частиц квантовой жидкости не могут пересекаться. В результате интерференция возникает как результат сложной картины рассеяния сталкивающихся потоков частиц, при котором их скорости достигают бесконечных значений.

Описанные математические особенности квантового гидродинамического описания выступают существенным препятствием к его использованию в прикладных расчётах. Тем не менее, существуют примеры его успешного использования как в применении к простейшим тестовым задачам, так и для описания некоторых молекулярных процессов [4]. [5]..

Люсьен Харди[6] и Дж. С. Белл[2] подчеркивают, что в картине квантовой механики де Бройля — Бома могут существовать «пустые волны», которые описываются волновыми функциями, распространяющимися в пространстве и времени, но не несущие энергию или импульс[7] и не привязанные к частице. Эта же концепция была названа «волной-призраком» (или «Gespensterfelder», полями-призраками) Альбертом Эйнштейном.[8]

Понятие пустой волновой функции обсуждалось подробно в литературе[9][10][11]. В многомировой интерпретации квантовой механики нет необходимости вводить понятие пустой волновой функции[2].