Теорема Монжа

Теорема Мо́нжа — теорема о трёх окружностях, сформулированная Жаном Д’Аламбером и доказанная Гаспаром Монжем. Часто используется как пример теоремы в доказательстве которой полезно повысить размерность пространства.

Теорема Монжа. Красным, синим и зелёным показаны пары общих внешних касательных.

Формулировка

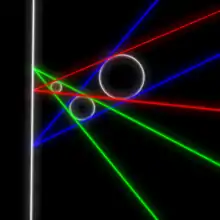
Для трёх произвольных окружностей, каждая из которых не лежит целиком внутри другой, точки пересечения общих внешних касательных к каждой паре окружностей лежат на одной прямой.

Доказательство

В простейшем доказательстве используется трехмерная аналогия.[1] Пусть три круга соответствуют трем сферам разного радиуса; круги соответствуют экваторам, которые возникают из плоскости, проходящей через центры сфер. Три сферы можно однозначно зажать между двумя плоскостями. Каждая пара сфер определяет конус, который касается обеих сфер снаружи, а вершина этого конуса соответствует точке пересечения двух внешних касательных, то есть внешнему центру подобия. Поскольку одна линия конуса лежит в каждой плоскости, вершина каждого конуса должна лежать в обеих плоскостях и, следовательно, где-то на линии пересечения двух плоскостей. Следовательно, три внешних центра гомотетики коллинеарны.

Вариации и обобщения
  • Если две поверхности второго порядка описаны или вписаны в третью поверхность второго порядка, то линия их пересечения распадается на две плоских кривые, плоскости которых проходят через прямую, проходящую через две точки пересечения линий касания.

См. также
  • Задача о покрытии полосками — другой классический пример утверждения в доказательстве которого полезно повысить размерность пространства.

Примечания
  1. Wells, David. The Penguin Dictionary of Curious and Interesting Geometry. — New York : Penguin Books, 1991. — P. 153–154. — ISBN 0-14-011813-6.

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.