Задача о покрытии полосками

В трёхмерном варианте задачи вместо полосок берутся области между параллельными плоскостями. Решение этого варианта задачи легко следует из того, что площадь боковой поверхности шарового слоя зависит только от его высоты. В частности, сферу нельзя покрыть слоями с общей толщиной, меньшей диаметра сферы, а значит, нельзя и шар.

Из этого наблюдения немедленно следует двумерный случай. Это решение было предложено Гуго Штейнгаузом.

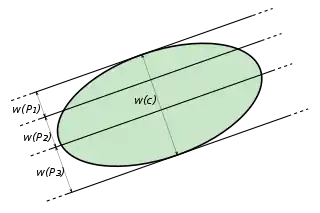
• В 1932 году Тарский выдвинул гипотезу, что если выпуклую фигуру можно покрыть полосками с общей шириной 1, то её можно покрыть одной полоской ширины 1. Утвердительный ответ получен Тёгером Бангом в 1951 году.[1]

• Следующий вариант задачи про относительную ширину полосок был предложен Бангом:

Предположим, выпуклое тело ${\displaystyle K}$ покрыто конечным числом полосок с ширинами ${\displaystyle w_{1},\dots ,w_{n}}$, и ${\displaystyle v_{1},\dots ,v_{n}}$ есть ширины ${\displaystyle K}$ в соответствующих направлениях. Доказать, что

${\displaystyle {\frac {w_{1}}{v_{1}}}+\dots +{\frac {w_{n}}{v_{n}}}\geq 1.}$

• Теорема Монжа — другой классический пример утверждения в доказательстве которого полезно повысить размерность пространства.

• И. М. Яглом. Т. Банг — В. Фенхель. Решение одной задачи о покрытии выпуклых фигур (рус.) // Матем. просв., сер. 2. — 1957. — № 1. — С. 214—218.
• R. Alexander. A problem about lines and ovals (англ.) // The American Mathematical Monthly. — 1968. — Vol. 75, no. 5. — P. 482—487.
• Bezdek, Károly. Tarski’s plank problem revisited // Geometry—intuitive, discrete, and convex. — 2013. — С. 45—64.
• Gardner, Richard. Relative width measures and the plank problem (англ.) // Pacific Journal of Mathematics. — 1988. — Vol. 135, no. 2. — P. 299—312.
• Bang, Thøger (1950), On covering by parallel-strips., Mat. Tidsskr. B.: 49–53
• Bang, Thøger (1951), A solution of the "plank problem", Proc. Amer. Math. Soc. Т. 2 (6): 990–993, doi:10.2307/2031721, <http://www.ams.org/journals/proc/1951-002-06/S0002-9939-1951-0046672-4/>