Список с пропусками

Список с пропусками (англ. Skip List) — вероятностная структура данных, основанная на нескольких параллельных отсортированных связных списках с эффективностью, сравнимой с двоичным деревом (порядка O(log n) среднее время для большинства операций).

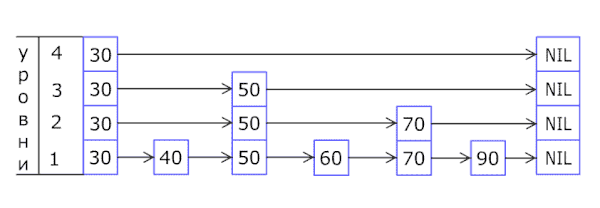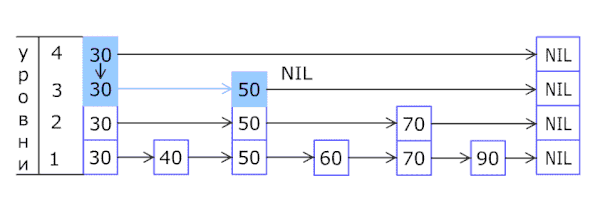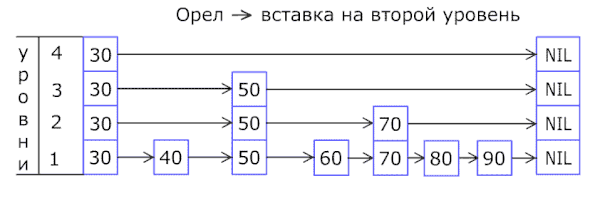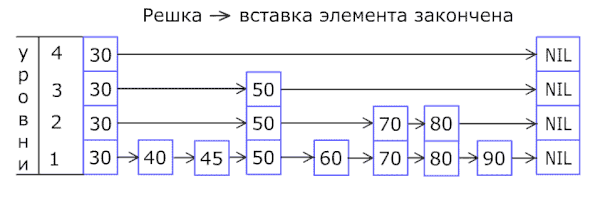
Вставка элемента в список с пропусками

В основе списка с пропусками лежит расширение отсортированного связного списка дополнительными связями, добавленными в случайных путях с геометрическим/негативным биномиальным распределением[1], таким образом, чтобы поиск по списку мог быстро пропускать части этого списка. Вставка, поиск и удаление выполняются за логарифмическое случайное время.

Описание

Список с пропусками — это несколько слоев. Нижний слой — это обычный упорядоченный связный список. Каждый более высокий слой представляет собой «выделенную полосу движения» для списков ниже, где элемент в i-м слое появляется в i+1-м слое с некоторой фиксированной вероятностью p (два наиболее часто используемых значений для p — 1/2 и 1/4). В среднем каждый элемент встречается в 1/(1-p) списках, и верхний элемент (обычно специальный головной элемент в начале списка с пропусками) в $\log _{1/p}n$ списках.

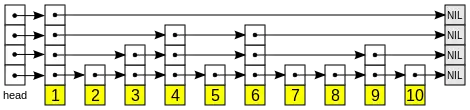
Поиск нужного элемента начинается с головного элемента верхнего списка, и выполняется горизонтально до тех пор, пока текущий элемент не станет больше либо равен целевому. Если текущий элемент равен целевому, он найден. Если текущий элемент больше, чем целевой, процедура повторяется после возвращения к предыдущему элементу и спуска вниз вертикально на следующий нижележащий список. Ожидаемое число шагов в каждом связном списке 1/p, что можно увидеть, просматривая путь поиска назад с целевого элемента, пока не будет достигнут элемент, который появляется в следующем более высоком списке. Таким образом, общие ожидаемые затраты на поиск — $(\log _{1/p}n)/p,$ , равные ${\mathcal {O}}(\log n)$ в случае константного p. Выбирая разные значения p, возможно выбирать необходимый компромисс между затратами на время поиска и затратами памяти на хранение списка.

Детали реализации

Элементы, используемые в списке с пропусками, могут содержать более одного указателя, таким образом они могут состоять в более чем одном списке.

Операции удаления и вставки реализованы весьма похоже на аналогичные операции связного списка, с тем исключением, что «высокие» должны быть вставлены или удалены более чем из одного связного списка.

Однако без рандомизации эти операции приводили бы к очень низкой производительности, так как необходимо было бы полностью перетасовывать список при добавлении нового элемента, чтобы сохранить число пропусков на верхнем уровне константным. William Pugh предложил следующий алгоритм для решения, на какую высоту должен быть продвинут новый элемент. Этот алгоритм требует лишь локальных изменений списка при добавлении новых элементов и позволяет сохранять эффективность «экспресс-линий» (l — результирующее значение уровня, на который нужно помещать элемент):

l = 1
пока случайное значение в диапазоне [0,1] < p и l < максимального уровня
  l = l + 1

В итоге элемент вставляет на l-й уровень и, соответственно, на все уровни меньше l.

Θ(n) операций, которые необходимы нам для посещения каждого узла в возрастающем порядке (например, печать всего списка), предоставляют возможность выполнить незаметную дерандомизацию структуры уровней списка с пропусками оптимальным путём, достигая ${\mathcal {O}}(\log n)$ времени поиска для связного списка. (выбирая уровень i-го конечного узла 1 плюс количество раз, которое мы можем поделить i на 2, пока оно не станет нечетным. Также i=0 для отрицательно бесконечного заголовка, как мы имеем, обычный специальный случай, выбирая максимально возможный уровень для отрицательных и/или положительных бесконечных узлов.) Тем не менее, это позволяет узнать кому-нибудь, где все узлы с уровнем более 1, и затем удалить их.

В качестве альтернативы мы можем сделать структуру уровней квази-случайной следующим путём:

создать все узлы уровня 1
j = 1
пока количество узлов на уровне j > 1
  для каждого i-го узла на уровне j
    если i нечетное 
      если i не последний узел на уровне j
        случайно выбираем, продвигать ли его на уровень j+1
      иначе
        не продвигать
      конец условия
    иначе, если i четный узел i-1 не продвинут
      продвинуть его на уровень j+1
    конец условия
  конец цикла для
  j = j + 1
конец цикла пока

Так же, как дерандомизированная версия, квази-рандомизация выполняется только, когда есть какая-то другая причина выполнять Θ(n) операций (которые посетят каждый узел).

Пример реализации

Код класса на C++

using std::swap;

template <typename KEY_T, typename DATA_T>
class SkipList{
	size_t MaxLevel;
	double SkipDivisor;
	struct Pair{
		KEY_T Key;
		DATA_T Data;
		Pair* Previous;
		Array<Pair*> Next;
		Pair(const KEY_T& InKey, const DATA_T& InData, Pair* InPrevious, size_t InLevel);
		Pair(size_t InLevel);
		~Pair();
		Pair& operator=(const Pair& InPair);
		Pair* PreviousOnLevel(size_t InLevel);
		Pair* NextOnLevel(size_t InLevel);
	};
	Pair Start;
	Pair* NewPrevious(const KEY_T& InKey);
	Pair* PairByKey(const KEY_T& InKey);
	size_t NewLevel();
public:
	class Iterator{
		SkipList* CurrentList;
		Pair* CurrentPair;
		friend class SkipList<KEY_T, DATA_T>;
	public:
		Iterator(const Iterator& InIterator);
		Iterator(SkipList& InSkipList);
		operator bool();
		Iterator& operator++();
		Iterator& operator--();
		Iterator operator++(int);
		Iterator operator--(int);
		Iterator& operator+=(size_t n);
		Iterator& operator-=(size_t n);
		Iterator& operator=(const Iterator& InIterator);
		Iterator& operator=(const KEY_T& InKey);
		DATA_T& operator*();
		void Delete();
	};
	SkipList(size_t InNumberOfLanes=3, double InSkipDivisor=1.0/4.0);
	~SkipList();
	Iterator GetBegin();
	Iterator GetEnd();
	void Add(const KEY_T& InKey, const DATA_T& InData);
	void Delete(const KEY_T& InKey);
	DATA_T& operator[](const KEY_T& InKey);
	size_t Count();
	void Clear();
	Iterator Find(const DATA_T& Unknown);
	bool IsEmpty();
};

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Pair* SkipList<KEY_T, DATA_T>::Pair::PreviousOnLevel(size_t InLevel){
	if(!this)
		return NULL;
	Pair* Current=Previous;
	for(; Current && !(Current->Next.Count()>=InLevel+1); Current=Current->Previous){}
	return Current;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Pair* SkipList<KEY_T, DATA_T>::Pair::NextOnLevel(size_t InLevel){
	if(!this)
		return NULL;
	Pair* Current=Next[InLevel-1];
	for(; Current && !(Current->Next.Count()>=InLevel+1); Current=Current->Next[InLevel-1]){}
	return Current;
}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::Pair::Pair(const KEY_T& InKey, const DATA_T& InData, SkipList<KEY_T, DATA_T>::Pair* InPrevious, size_t InLevel):Key(InKey), Data(InData), Previous(InPrevious){
	Pair* Current=Previous->Next[0];
	Next.AddLast(Current);
	for(size_t Counter=1; Counter<=InLevel; Counter++){
		Current=NextOnLevel(Counter);
		Next.AddLast(Current);
	}
	Current=Previous;
	for(size_t Counter=0; Counter<=InLevel; Counter++)
		if(Current=PreviousOnLevel(Counter))
			Current->Next[Counter]=this;
}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::Pair::Pair(size_t InLevel): Previous(NULL){
	for(size_t Counter=0; Counter<=InLevel; Counter++)
		Next.AddLast(NULL);
}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::Pair::~Pair(){
	size_t OurLevel=Next.Count()-1;
	Pair* Current=this;
	for(size_t Counter=0; Counter<=OurLevel; Counter++)
		if(Current=PreviousOnLevel(Counter))
			Current->Next[Counter]=Next[Counter];
}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::SkipList(size_t InMaxLevel, double InSkipDivisor):MaxLevel(InMaxLevel), SkipDivisor(InSkipDivisor),Start(MaxLevel){}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Pair& SkipList<KEY_T, DATA_T>::Pair::operator=(const SkipList<KEY_T, DATA_T>::Pair& InPair){
	Key=InPair.Key;
	Data=InPair.Data;
	Previous=InPair.Previous;
	size_t max=Next.Count();
	for(size_t i; i<max; ++i)
		Next.AddLast(Next[i]);
	return *this;
}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::~SkipList(){
	Clear();
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Pair* SkipList<KEY_T, DATA_T>::NewPrevious(const KEY_T& InKey){
	Pair* Previous=&Start;
	Pair* Current=Start.Next[MaxLevel];
	for(size_t Counter=MaxLevel; Counter>=0; Counter--){
		while(Current && InKey>Current->Key){
			Previous=Current;
			Current=Current->Next[Counter];
		}
		if(!Counter)
			break;
		Current=Previous;
	};
	return Previous;
}

template <typename KEY_T, typename DATA_T>
size_t SkipList<KEY_T, DATA_T>::NewLevel(){
	size_t Level=0;
	while(rand()%1000<SkipDivisor*1000 && Level<=MaxLevel)
		Level++;
	return Level;
}

template <typename KEY_T, typename DATA_T>
void SkipList<KEY_T, DATA_T>::Add(const KEY_T& InKey, const DATA_T& InData){
	Pair* Previous=NewPrevious(InKey);
	Pair* Next=Previous->Next[0];
	if(Next && Next->Key==InKey)
		throw String("Not unique key!");
	new Pair(InKey, InData, Previous, NewLevel());
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Pair* SkipList<KEY_T, DATA_T>::PairByKey(const KEY_T& InKey){
	Pair* Current=NewPrevious(InKey);
	if((Current=Current->Next[0]) && Current->Key==InKey)
		return Current;
	throw String("No pair for this key!");
}

template <typename KEY_T, typename DATA_T>
void SkipList<KEY_T, DATA_T>::Delete(const KEY_T& InKey){
	if(IsEmpty())
		throw String("There is empty list!");
	delete PairByKey(InKey);
}

template <typename KEY_T, typename DATA_T>
DATA_T& SkipList<KEY_T, DATA_T>::operator[](const KEY_T& InKey){
	if(IsEmpty())
		throw String("List is empty!");
	return PairByKey(InKey)->Data;
}

template <typename KEY_T, typename DATA_T>
size_t SkipList<KEY_T, DATA_T>::Count(){
	if(IsEmpty())
		return 0;
	Pair* Next=Start.Next[0];
	size_t n=1;
	while(Next=Next->Next[0])
		n++;
	return n;
}

template <typename KEY_T, typename DATA_T>
void SkipList<KEY_T, DATA_T>::Clear(){
	Pair* Current=Start.Next[1];
	Pair* Previous=NULL;
	while(Current){
		Current->Previous=NULL;
		Previous=Current;
		Current=Current->Next[0];
		delete Previous;
	}
	for(size_t i=0; i<=Start.Next.Count()-1;i++)
		Start.Next[i]=NULL;
}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::Iterator::Iterator(const SkipList<KEY_T, DATA_T>::Iterator& InIterator):CurrentList(InIterator.CurrentList), CurrentPair(InIterator.CurrentPair){}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::Iterator::Iterator(SkipList<KEY_T, DATA_T>& InSkipList):CurrentList(&InSkipList), CurrentPair(InSkipList.Start.Next[0]){}

template <typename KEY_T, typename DATA_T>
SkipList<KEY_T, DATA_T>::Iterator::operator bool(){
	return CurrentList && CurrentPair;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator& SkipList<KEY_T, DATA_T>::Iterator::operator++(){
	if(CurrentPair)
		CurrentPair=CurrentPair->Next[0];
	return *this;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator& SkipList<KEY_T, DATA_T>::Iterator::operator--(){
	if(CurrentPair && CurrentPair!=CurrentList->Start.Next[0])
		CurrentPair=CurrentPair->Previous;
	else
		CurrentPair=NULL;
	return *this;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator SkipList<KEY_T, DATA_T>::Iterator::operator++(int){
	Iterator Old(*this);
	++*this;
	return Old;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator SkipList<KEY_T, DATA_T>::Iterator::operator--(int){
	Iterator Old(*this);
	--*this;
	return Old;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator& SkipList<KEY_T, DATA_T>::Iterator::operator=(const SkipList<KEY_T, DATA_T>::Iterator& InIterator){
	CurrentList=InIterator.CurrentList;
	CurrentPair=InIterator.CurrentPair;
	return *this;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator& SkipList<KEY_T, DATA_T>::Iterator::operator=(const KEY_T& InKey){
	CurrentPair=CurrentList->PairByKey(InKey);
	return *this;
}

template <typename KEY_T, typename DATA_T>
DATA_T& SkipList<KEY_T, DATA_T>::Iterator::operator*(){
	if(!*this)
		throw String("Reading from bad iterator!");
	return CurrentPair->Data;
}

template <typename KEY_T, typename DATA_T>
void SkipList<KEY_T, DATA_T>::Iterator::Delete(){
	if(!*this)
		throw String("Deleting data of bad iterator!");
	delete CurrentPair;
	CurrentPair=NULL;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator& SkipList<KEY_T, DATA_T>::Iterator::operator+=(size_t n){
	for(size_t Counter=0; Counter<n && CurrentPair; Counter++)
		CurrentPair=CurrentPair->Next[0];
	return *this;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator& SkipList<KEY_T, DATA_T>::Iterator::operator-=(size_t n){
	for(size_t Counter=0; Counter<n && CurrentPair; Counter++)
		CurrentPair=CurrentPair->Previous;
	if(CurrentPair==&CurrentList->Start)
	return *this;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator SkipList<KEY_T, DATA_T>::GetBegin(){
	return Iterator(*this);
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator SkipList<KEY_T, DATA_T>::GetEnd(){
	Iterator ReturnValue(*this);
	ReturnValue+=ReturnValue.CurrentList->Count()-1;
	return ReturnValue;
}

template <typename KEY_T, typename DATA_T>
typename SkipList<KEY_T, DATA_T>::Iterator SkipList<KEY_T, DATA_T>::Find(const DATA_T& Unknown){
	Iterator Result(*this);
	while (Result&& !(*Result==Unknown))
		++Result;
	return Result;
}

template <typename KEY_T, typename DATA_T>
bool SkipList<KEY_T, DATA_T>::IsEmpty(){
	typename Array<Pair*>::Iterator i(Start.Next);
	while(i)
		if(*i++)
			return false;
	return true;
}

Примечания

Pugh, William. Skip lists: a probabilistic alternative to balanced trees (англ.) // Communications of the ACM : journal. — 1990. — June (vol. 33, no. 6). — P. 668—676. — doi:10.1145/78973.78977.

Литература

William Pugh. Skip Lists: A Probabilistic Alternative to Balanced Trees / Workshop on Algorithms and Data Structures. Springer Berlin Heidelberg, 1989; Communications of the ACM CACM Homepage archive Volume 33 Issue 6, June 1990 Pages 668-676 doi:10.1145/78973.78977 — оригинальная работа
Маннинг К., Рагхаван П., Шютце Х. Введение в информационный поиск. — Вильямс, 2011. — 512 с. — ISBN 978-5-8459-1623-5.

Ссылки

Skip List Applet by Kubo Kovac
Skip List Applet — Portuguese (недоступная ссылка) by Jackson Porciúncula (very good)
Skip list description from the Dictionary of Algorithms and Data Structures
A Skip List in C#
SkipDB, a BerkeleyDB-style database implemented using skip lists.
Thomas Wenger’s demo applet on skiplists
A Java Applet that emphasizes more on visualizing the steps of the algorithm
Prof. Erik Demaine’s lecture on skip lists from MIT’s OpenCourseWare program. (Audio)
Java 6 ConcurrentSkipListSet
John Shipman’s didactic zero-defect implementation in Python
An Extensive Examination of Data Structures Using C# 2.0: Building a Better Binary Search Tree
C# Skip List: A Simpler Alternative to Binary Trees?

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Pugh, William. Skip lists: a probabilistic alternative to balanced trees (англ.) // Communications of the ACM : journal. — 1990. — June (vol. 33, no. 6). — P. 668—676. — doi:10.1145/78973.78977.

Структуры данных
Списки	Массив Односвязный список Двусвязный список Список с пропусками
Деревья	B-дерево Двоичное дерево поиска AVL-дерево Красно-чёрное дерево Куча
Графы	Ориентированный граф Ориентированный ациклический граф Бинарная диаграмма решений Гиперграф
Прочие	Хеш-таблица Стек