Система физических величин

Систе́ма физи́ческих величи́н (далее СФВ) — совокупность взаимосвязанных физических величин, образованная по принципу, когда одни физические величины являются независимыми (основными физическими величинами), а другие являются их функциями (производными физическими величинами). СФВ представляет собой структурную схему связей или алгебраическую диаграмму операторов физических величин. Эти связи описываются математическими выражениями, называемыми определяющими уравнениями.[1][2]

Примеры СФВ

1. Международная система величин (фр. International Système de grandeurs, англ. International System of Quantities, ISQ). Использует размерные электрическую и магнитную постоянные и рационализированную запись формул (в уравнениях Максвелла отсутствует коэффициент 4π).

В качестве основных физических величин в ISQ используются:

Когерентной системой единиц для ISQ является Международная система единиц СИ.

2. Периодическая таблица законов в физике Бартини

L — пространство,
T — время.

Свою гипотезу для отношения между фундаментальными физическими константами Бартини попытался (возможно в шутливой форме[3]) описать в своей статье.[4][5]

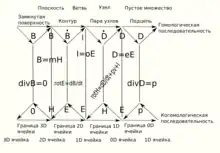
Алгебраическая диаграмма уравнений Максвелла для электромагнитного поля (Крон, Рос)

3. Коммутативная диаграмма Крона или СФВ вводит понятие многогранных алгебраических диаграмм и 8 тензоров:

e_a — электрическое напряжение,
b'_a — сила тока,
h^a — приложенное электрическое напряжение,
d'^a — приложенная сила тока,
E_a — напряжённость электрического поля,
B'_a — магнитная индукция,
H^a — напряжённость магнитного поля,
D'^a — электрическое смещение.

Которые соответствуют физическим величинам из законов Кирхгофа и уравнений Максвела. Он применяет СФВ для метода многогранников (обобщение линейного метода Крона для электрических машин для случая распространения волн через сами машины или пространственные фильтры). Одна стрелка на многогранной диаграмме соответствует тензору c октонионами (многогранной совокупности тензоров).[2]

СФВ тесно связаны с задачами моделирования и описания физической реальности[6] на языке Verilog-AMS.

На практике термин «СФВ» применяется редко. Обычно говорят о формулах в системах единиц (СИ, СГС и т. д.), даже если в исследовании единицы измерения и числовые значения величин не используются.

Системы единиц физических величин

С понятием СФВ тесно связано понятие системы единиц физических величин (СЕФВ). Система единиц называется когерентной для данной системы величин, если единицы измерения производных величин (производные единицы) в системе единиц когерентны, то есть представляют собой произведения степеней единиц основных величин (основных единиц) с коэффициентами пропорциональности, равными единице.

Примечания

В. Брагин, В. Панков. Прогнозатор Вудынского - машина предсказывающая не открытые законы // Изобретатель и рационализатор. — 1973. — № 1.
Исследование сложных систем по частям - диакоптика, 1972, с. 511.
В. И. Арнольд. Истории давние и недавние. — М.: ФАЗИС, 2002. — 96 с. — ISBN 5-7036-0077-4.
П. Г. Кузнецов, Р. О. ди Бартини. О множественности геометрий и множественности физик (рус.) // Проблемы и особенности современной научной методологии : журнал. — 1978. — С. 54—65.
Р. О. ди Бартини. Соотношения между физическими величинами (рус.) // Проблемы теории гравитации и элементарных частиц. — 1966. — С. 249—266.
Riesz M. Clifford Numbers and Spinors: With Riesz’s Private Lectures to E. Folke Bolinder and a Historical Review by Pertti Lounesto.. — Dordrect/Boston/London: Kluwer Academic Publisher, 1993.

Литература

Г. Крон. Исследование сложных систем по частям - диакоптика. — Москва: Наука, 1972. — 544 с.

См. также

Ссылки

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[bragin-1] В. Брагин, В. Панков. Прогнозатор Вудынского - машина предсказывающая не открытые законы // Изобретатель и рационализатор. — 1973. — № 1.

[_160abbdc05e54dee-2] Исследование сложных систем по частям - диакоптика, 1972, с. 511.

[3] В. И. Арнольд. Истории давние и недавние. — М.: ФАЗИС, 2002. — 96 с. — ISBN 5-7036-0077-4.

[4] П. Г. Кузнецов, Р. О. ди Бартини. О множественности геометрий и множественности физик (рус.) // Проблемы и особенности современной научной методологии : журнал. — 1978. — С. 54—65.

[5] Р. О. ди Бартини. Соотношения между физическими величинами (рус.) // Проблемы теории гравитации и элементарных частиц. — 1966. — С. 249—266.

[6] Riesz M. Clifford Numbers and Spinors: With Riesz’s Private Lectures to E. Folke Bolinder and a Historical Review by Pertti Lounesto.. — Dordrect/Boston/London: Kluwer Academic Publisher, 1993.