Прямая Обера

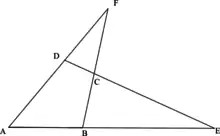
Прямая Обера (четырёхсторонника) — прямая, на которой лежат четыре ортоцентра четырёх треугольников, образованных четырьмя попарно пересекающимися прямыми, никакие три из которых не проходят через одну точку. Здесь используются те же четыре треугольника, что и при построении точки Микеля.

Полный четырёхсторонник

Существование прямой Обера обосновывается тем, что совпадают четыре прямых Симсона у этих треугольников.

Другими словами, прямая Обера полного четырёхсторонника является радикальной осью двух окружностей, построенных на его диагоналях как на диаметрах.

Последнее утверждение можно сформулировать в следующем виде. Пусть ${\displaystyle ABCD}$ — четырёхугольник, прямые ${\displaystyle AB}$ и ${\displaystyle CD}$ пересекаются в точке ${\displaystyle F}$, ${\displaystyle BC}$ и ${\displaystyle AD}$ — в ${\displaystyle E}$. Тогда окружности, построенные на отрезках ${\displaystyle AC}$, ${\displaystyle BD}$ и ${\displaystyle EF}$, как на диаметрах, имеют общую радикальную ось, на которой лежат 4 ортоцентра (4 точки пересечения высот) треугольников ${\displaystyle ABE}$, ${\displaystyle CDE}$, ${\displaystyle BCF}$ и ${\displaystyle ADF}$ (прямая Обера — Штейнера).

Как хорошо известно, последняя упомянутая прямая Обера — Штейнера есть директриса параболы, касающейся всех 4 сторон данного полного четырёхсторонника или вневписанной в него[1].