Построение Хайоша

Применение построения Хайоша для двух копий K₄ путём объединения вершин из двух копий графа в одну вершину (показана двумя цветами), удаления вершин, инцидентных объединённой вершине в каждом подграфе (показаны пунктиром) и добавления нового ребра, соединяющего конечные вершины удалённых вершин (показано зелёным цветом), в результате чего получаем веретено Мозера.

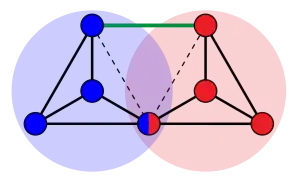
Пусть G и H — два неориентированных графа, vw — ребро графа G, а xy — ребро графа H. Тогда построение Хайоша образует новый граф, комбинирующий два графа путём объединения вершин v и x в одну вершину, удаления рёбер vw и xy и добавления нового ребра wy.

Например, пусть G и H — два полных графа K₄ с четырьмя вершинами. Ввиду симметрии этих графов выбор рёбер в этих графах несущественен. В этом случае результатом применения построения Хайоша будет веретено Мозера, граф единичных расстояний с семью вершинами, требующий для раскраски четыре цвета.

Другой пример, если G а H — два цикла длины p и q соответственно, то результатом применения построения Хайоша будет снова цикл длины p + q − 1.

Говорят, что граф G k-конструируемый (или k-конструируемый по Хайошу), если он образован одним из трёх способов [2]:

• Полный граф K_k является k-конструируемым.
• Пусть G и H — два k-конструируемых графа. Тогда граф, образованный применением построения Хайоша к G и H, является k-конструируемым.
• Пусть G — любой k-конструируемый граф, и пусть u и v — любые две несмежные вершины в G. Тогда граф, образованный объединением u и v в одну вершину, также является k-конструируемым. Эквивалентно, этот граф может быть построен добавлением ребра uv к графу, а затем стягиванием его.

Достаточно просто показать, что любой k-конструируемый граф требует по меньшей мере k цветов для правильной раскраски графа. В самом деле, это совершенно ясно для полного графа K_k, а результат объединения двух несмежных вершин вынуждает раскрасить их в один цвет в любой раскраске, что не уменьшает числа цветов. В самом построении Хайоша новое ребро wy заставляет по меньшей мере одну из двух вершин w и y иметь цвет, отличный от цвета вершины, полученной объединением вершин v and x, так что любая правильная раскраска комбинированного графа приводит к правильной раскраске одного из двух меньших графов, из которых граф был получен, откуда опять получаем необходимость k цветов[2].

Хайош доказал более строгое утверждение, что граф требует по меньшей мере k цветов в любой правильной раскраске тогда и только тогда, когда он содержит k-конструируемый граф в качестве подграфа. Эквивалентно, любой k-критический граф (граф, требующий k цветов, но любой собственный подграф требует меньше цветов) является k-конструируемым[3]. Альтернативно, любой граф, требующий k цветов, может быть образован комбинированием построения Хайоша, операциями объединения двух несмежных вершин и операциями добавления вершин или рёбер к заданному графу, начав с полного графа K_k[4].

Аналогичное построение может быть использовано для предписанной раскраски вместо обычной раскраски[5][6].

Для k=3 любой k-критический граф (то есть любой нечётный цикл) может быть построен как k-конструируемый граф таким образом, что все графы, образованные при его построении, являются также k-критическими. Для k=8 это неверно — граф, который нашёл Катлин[7] в качестве контрпримера гипотезе Хадвигера, что k-хроматический граф стягиваем к полному графу K_k, является контрпримером для этой задачи. Впоследствии были найдены k-критические, но не k-конструируемые графы лишь исключительно через k-критические графы, для всех k ≥ 4. Для k=4 один такой пример получается из графа додекаэдра путём добавления нового ребра к каждой паре антиподальных вершин[8].

Поскольку объединение двух несмежных вершин уменьшает число вершин в результирующем графе, число операций, необходимых для представления заданного графа G с использованием операций, определённых Хайошем, не может превзойти числа вершин графа G[9].

Мэнсфилд и Уэлш [10] определяют число Хайоша h(G) k-хроматического графа G как минимальное число шагов, необходимых для построения G из K_k, где на каждом шаге образуется новый граф путём комбинации двух сформированных ранее графов, объединения двух несмежных вершин сформированного ранее графа или добавления ребра к сформированному ранее графу. Они показали, что для графа G с n вершинами и m рёбрами h(G) ≤ 2^{n2/3 − m + 1} − 1. Если любой граф имеет полиномиальное число Хайоша, отсюда следует, что можно доказать нераскрашиваемость за недетерминированное полиномиальное время, а потому следует, что NP = co-NP, что считают невероятным теоретики сложности алгоритмов[11]. Однако неизвестно, как доказать неполиномиальные нижние границы чисел Хайоша без некоторых предположений о теоретической сложности, и если такие границы будут доказаны, немедленно будет следовать существование неполиномиальных границ некоторых типов систем Фреге в математической логике[11].

Минимальный размер дерева выражений, описывающего построение Хайоша для заданного графа G, может быть существенно больше, чем число Хайоша графа G, поскольку наименьшее выражение для G может использовать повторно те же графы несколько раз (экономия не разрешена в дереве выражений). Существует 3-хроматические графы, для которых наименьшее такое дерево выражений имеет экспоненциальный размер[12].

Кёстер[13] использовал построение Хайоша для получения бесконечного множества 4-критичных полиэдральных графов, каждый из которых имеет вдвое больше рёбер, чем вершин. Подобным же образом Лю и Чжан[14] использовали построение, начинающееся с графа Грёча, чтобы получить много 4-критичных графов без треугольников, для которых, как они показали, трудно найти раскраску с помощью традиционных алгоритмов поиска с возвратом.

В комбинаторике многогранников Рейнхард Эйлер[15] использовал построение Хайоша для генерации фасет устойчивого множества политопа.