Критический граф
Критический граф — граф, в котором удаление любой вершины или ребра приводит к уменьшению хроматического числа графа.

Вверху слева вершинно критический граф с хроматическим числом 6. Остальные N-1 подграфов имеют хроматическое число 5.
Связанные определения
- -критический граф — это критический граф с хроматическим числом k.
- Граф G с хроматическим числом k является вершинно k-критическим, если каждая из его вершин является критическим элементом [1].
Свойства
- Пусть G есть k-критический граф с n вершинами и m рёбрами. Тогда:
- G имеет только одну компоненту.
- G конечен (теорема де Брёйна — Эрдёша [2]).
- δ(G) ≥ k − 1, то есть любая вершина смежна по меньшей мере k − 1 другим вершинам. Более строго, G рёберно (k − 1)-связен [3].
- Если граф G (k − 1)-регулярен (каждая вершина смежна в точности k − 1 другим), то граф G либо является полным графом Kk, либо нечётным циклом. (Это теорема Брукса[4]).
- 2 m ≥ (k − 1) n + k − 3 [5].
- 2 m ≥ (k − 1) n + [(k − 3)/(k2 − 3)] n [6].
- Либо G может быть разбит на два меньших критических графа с ребром между каждой парой вершин, где две вершины берутся из разных частей, либо граф G имеет по меньшей мере 2k — 1 вершин[7]. Более строго, либо G имеет разложения такого типа, либо для каждой вершины v графа G существует k-раскраска, в которой v является единственной вершиной со своим цветом, а все остальные классы цветов имеют по меньшей мере две вершины[8].
- Граф G является вершинно критическим тогда и только тогда, когда для любой вершины v существует оптимальная подходящая раскраска, в которой вершина v одна представляет класс цвета.
- 1-критических графов не существует.
- Единственный 2-критический граф — это K2.
- Все 3-критические графы исчерпываются простыми циклами нечётной длины[9].
- Как показал Хаджос[10], любой k-критический граф может быть сформирован из полного графа Kk путём комбинации построения Хайоша с операцией отожествления двух несмежных вершин. Граф, образованный таким образом, всегда требует k цветов в любой правильной раскраске.
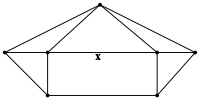
4-критический, но не рёберно-критический граф, поскольку
- Хотя каждый рёберно-критический граф обязательно является критическим, обратное неверно. Например, граф представленный справа, является 4-критическим, но не рёберно-критическим[11].
Вариации и обобщения
- Дважды критический граф — это связный граф, в котором удаление любой пары смежных вершин уменьшает хроматическое число на два. Одна из нерешённых задач — является ли Kk единственным дважды критическим k-хроматическим графом[12].
См. также
Примечания
- Следует отметить, что не всегда под критическим графом понимается критический k-хроматический граф. В статье Визинга под критическим графом размерности k понимается граф, у которого размерность любой собственной части меньше k. Под размерностью графа при этом понимается минимальная размерность метрического пространства, в которое можно вложить граф так, что все смежные вершины окажутся на расстоянии 1. (Визинг 1968)
- de Bruijn, Erdős, 1951.
- Lovász, 1992.
- Brooks, Tutte, 1941.
- Dirac, 1957.
- Gallai, 1963a.
- Gallai, 1963b.
- Stehlík, 2003.
- Харари, 2003, с. 167.
- Hajós, 1961.
- Харари, 2003, с. 168-169.
- Erdős, 1966.
Литература
- R. L. Brooks, W. T. Tutte. On colouring the nodes of a network // Proceedings of the Cambridge Philosophical Society. — 1941. — Т. 37, вып. 02. — С. 194–197. — doi:10.1017/S030500410002168X.
- N. G. de Bruijn, P. Erdős. A colour problem for infinite graphs and a problem in the theory of relations // Nederl. Akad. Wetensch. Proc. Ser. A. — 1951. — Т. 54. — С. 371–373.. (Indag. Math. 13.)
- G. A. Dirac. A theorem of R. L. Brooks and a conjecture of H. Hadwiger // Proceedings of the London Mathematical Society. — 1957. — Т. 7, вып. 1. — С. 161–195. — doi:10.1112/plms/s3-7.1.161.
- T. Gallai. Kritische Graphen I // Publ. Math. Inst. Hungar. Acad. Sci.. — 1963a. — Т. 8. — С. 165–192.
- T. Gallai. Kritische Graphen II // Publ. Math. Inst. Hungar. Acad. Sci.. — 1963b. — Т. 8. — С. 373–395..
- G. Hajós. Über eine Konstruktion nicht n-färbbarer Graphen // Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg Math.-Natur. Reihe. — 1961. — Т. 10. — С. 116–117.
- T. R. Jensen, B. Toft. Graph coloring problems. — New York: Wiley-Interscience, 1995. — ISBN 0-471-02865-7.
- Matěj Stehlík. Critical graphs with connected complements // Journal of Combinatorial Theory. — 2003. — Т. 89, вып. 2. — С. 189–194. — doi:10.1016/S0095-8956(03)00069-8.
- László Lovász. Combinatorial Problems and Exercises (Second Edition). — North-Holland, 1992.
- Paul Erdős. In Theory of Graphs. — Proc. Colloq., Tihany, 1966. — С. 361.
- В. Г. Визинг. Некоторые нерешенные задачи в теории графов // Успехи Математических Наук. — 1968. — Т. XXIII, вып. 6 (144). — С. 117–134.
- Ф. Харари. Теория графов. — 2-е. — М.: Едиториал УРСС, 2003. — ISBN 5-354-00301-6, ББК 22.144, 22.18, 22.19.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
