Последовательно-параллельный частичный порядок
Последовательно-параллельный частичный порядок — это частично упорядоченное множество, построенное из меньших последовательно-параллельных частичных порядков с помощью двух простых операций соединения[1][2].
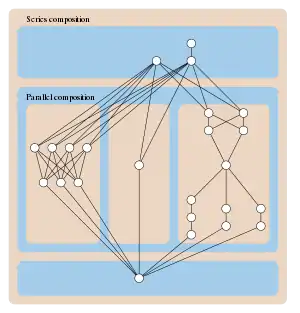
Последовательно-параллельные частичные порядки можно описать как свободные от N-порядка конечные частичные порядки. Они имеют порядковую размерность максимум два[1][3]. Эти порядки включают слабые упорядочения и отношение достижимости в ориентированных деревьях и ориентированных параллельно-последовательных графах[2][3]. Графы сравнимости последовательно-параллельных частичных порядков — это кографы[2][4].
Последовательно-параллельные частичные порядки применяются в теории расписаний[5], машинном обучении последовательностей событий во временны́х рядах данных[6], последовательности передачи мультимедийных данных[7] и максимизации пропускной способности в потоках данных[8].
Последовательно-параллельные частичные порядки называются также мультидеревьями[4]. Однако это название двусмысленно — мультидеревьями также называют частичные порядки без четырёхэлементых подпорядков («алмазов») [9], а также другие структуры, образованные из нескольких деревьев.
Определение
Пусть P и Q — два частично упорядоченных множеств. Последовательное соединение P и Q, записывется P; Q[7], P * Q[2], или P ⧀ Q[1], является частично упорядоченным множеством, элементы которого являются дизъюнктным объединением элементов P и Q. В P; Q, два элемента x и y, принадлежащих одновременно P или Q, имеют то же самое отношение порядка, которое они имели в P или Q соответственно. Однако для любой пары x, y, в которой x принадлежит P, а y принадлежит Q, имеется дополнительное отношение порядка x ≤ y, определяемое последовательным соединением. Последовательное соединение является ассоциативной оерацией — можно записать P; Q; R как последовательное соединение трёх порядков без внесения двусмысленности о том, как комбинировать их попарно, поскольку взятие в скобки (P; Q); R и P; (Q; R) описывает один и тот же частичный порядок. Однако это соединение не является коммутативной операцией, поскольку перестановка ролей P и Q даст другой частичный порядок, в котором отношения порядка для пар элементов, одного из P, другого из Q, обращаются[1].
Параллельное соединение P и Q, записывается P || Q[7], P + Q[2] или P ⊕ Q[1], определяется из несвязного объединения элементов P и элементов Q похожим образом. Если пара элементов принадлежит полностью P или Q, порядок остаётся тем же самым, что и был в P или Q соответственно. Если элемент x принадлежит P, а элемент y принадлежит Q, элементы x и y несравнимы. Параллельное соединение ассоциативно и коммутативно[1].
Класс последовательно-параллельных частичных порядков является множеством частичных порядков, которое может быть построено из одноэлементных частичных порядков с использованием этих двух операций. Эквивалентно, класс является наименьшим множеством частичных порядков, который включает одноэлементный частичный порядок и который замкнут по операциям последовательного и параллельного соединения[1][2].
Слабое упорядочение — это последовательно-параллельный частичный порядок, полученный в результате последовательности операций соединения, в котором сначала проведены все операции параллельного соединения, а затем результаты этих операций комбинированы с только последовательными операциями[2].
Описание запрещёнными подпорядками
Частичный порядок N с четырьмя элементами a, b, c и d и в точности тремя отношениями порядка a ≤ b ≥ c ≤ d является примером забора (или зигзаг-порядка). Его диаграмма Хассе имеет вид заглавной латинской буквы "N". Этот порядок не является последовательно-параллельным, поскольку нет способа разбить его на последовательности параллельных соединений двух меньших частичных порядков. Говорят, что частичный порядок P является свободным от N-порядка, если не существует множества из четырёх элементов в P, таких, что сужение P на эти элементы изоморфно N в смысле частичного порядка. Последовательно-параллельные частичные порядки являются в точности теми непустыми конечными свободными от N-порядка частичными порядками[1][2][3].
Отсюда немедленно следует (хотя это можно доказать и непосредственно), что любое непустое сужение последовательно-параллельного частичного порядка является само по себе последовательно-параллельным частичным порядком[1].
Порядковая размерность
Порядковая размерность частичного порядка P является минимальным размером реализаций P, множестве линейных продолжений (линеаризаций) порядка P со свойством, что для любых двух различных элементов x и y порядка P выполняется x ≤ y тогда и только тогда, когда x предшествует y в любом линейном продолжении реализации.
В интернете можно найти альтернативное определение: «Наименьшее число линейных порядков, дающих в пересечении данное частично упорядоченное множество, называется его (порядковой размерностью)», например в лекциях Гурова С.И.[10] или Кузнецова С.О.[11].
Последовательно-параллельные частичные порядки имеют размерность, не превосходящую двух. Если P и Q имеют реализаторы {L1, L2} и {L3, L4} соответственно, то {L1L3, L2L4} является реализатором последовательного соединения P; Q, а {L1L3, L4L2} является реализатором параллельного соединения P || Q[2][3]. Частичный порядок является последовательно-параллельным тогда и только тогда, когда он имеет реализатор, в котором одна из двух перестановок идентична, а вторая является отделимой.
Известно, что частичный порядок P имеет порядковую размерность два тогда и только тогда, когда существует сопряжённый порядок Q на тех же элементах со свойством, что любые два различных элементах x и y сравнимы в точности в одном из этих порядков. В случае серийно-параллельных частичных порядков сопряжённый порядок, являющийся сам по себе является последовательно-параллельным, может быть получен путём осуществления последовательности операций соединения в том же порядке, как и для P на тех же элементах, но вместо последовательного соединения в P используется параллельное соединение и наоборот. Более строго, хотя частичный порядок может иметь различные сопряжённые порядки, любой сопряжённый порядок последовательно-параллельного частичного порядка должен также быть последовательно-параллельным[2].
Связь с теорией графов
Любой частичный порядок может быть представлен (обычно не однозначно) направленным ациклическим графом, в котором имеется путь от x к y для всех элементов x и y частичного порядка, для которых выполняетсяx ≤ y. Графы, которые представляют последовательно-параллельные частичные порядки описанным образом, называются вершинными последовательно-параллельными графами и их транзитивные сокращения (графы отношений покрытия частичного порядка) называются минимальными вершинными последовательно-параллельными графами[3]. Ориентированные деревья и (с одной терминальной парой) параллельно-последовательные графы являются примерами минимальных последовательно-параллельных графов. Таким образом, последовательно-параллельные частичные порядки могут быть использованы для представления отношения достижимости в ориентированных деревьях и параллельных графах[2][3].
Граф сравнимости частичного порядка является неориентированным графом с вершинами для каждого элемента и неориентированным ребром для каждой пары различных элементов x, y, если x ≤ y или y ≤ x. То есть он образован из минимального последовательно-параллельного графа путём избавления от ориентации рёбер. Граф сравнимости последовательно-параллельного порядка является кографом — последовательные и параллельные операции соединения параллельного порядка дают операции на графе сравнимости, которые образуют несвязное объединение двух подграфов или соединяют два подграфа всеми возможными рёбрами. Эти две операции являются базовыми операциями в определении кографов. Обратно, любой кограф является графом сравнимости последовательно-параллельного частичного порядка. Если частичный порядок имеет кограф в качестве графа сравнимости, то он должен быть последовательно-параллельным частичным порядком, поскольку любой другой вид частичного порядка имеет N-подпорядок, который должен соответствовать порождённым путём с четырьмя вершинами в его графе сравнимости, а такие пути запрещены в кографах[2][4].
Вычислительная сложность
Можно использовать описание запрещёнными подпорядками последовательно-параллельных частичных порядков как базис для алгоритма, который проверяет за время, линейно зависящее от числа пар в соотношении, является ли заданное бинарное отношение последовательно-параллельным частичным порядком[2][3]. Альтернативно, если частичный порядок описывается как порядок достижимости направленного ациклического графа, возможно проверить, является ли он последовательно-параллельным частичным порядком, и если является, вычислить его транзитивное замыкание за время, пропорциональное числу вершин и рёбер в транзитивном замыкании. Остаётся открытым вопрос, можно ли улучшить время распознавания последовательно-параллельных порядков достижимости до линейного от размера входного графа[12].
Если последовательно-параллельный частичный порядок представлен как дерево выражений, описывающее выполнение последовательных и параллельных операций, то элементы частичного порядка могут быть представлены листьями дерева выражений. Сравнение двух любых элементов может быть осуществлено алгоритмически путём поиска наименьшего общего предка соответствующих двух листьев. Если этот предок является параллельным соединением, два элемента несравнимы, в противном случае порядок последовательных соединений операндов определяет порядок элементов. Таким способом последовательно-параллельный частичный порядок из n элементов может быть представлен в пространстве O(n) для определения любого сравниваемого значения с временем O(1)[2].
Задача проверки для двух заданных последовательно-параллельных частичных порядков P и Q, что P содержит сужение, изоморфное Q, является NP-полной[3].
Хотя задача подсчёта числа линейных продолжений произвольного частичного порядка является #P-полной[13], можно показать, что она может быть решена за полиномиальное время для последовательно-параллельных частичных порядков. А именно, если L(P) обозначает число линейных продолжений частичного порядка P, то L(P; Q)=L(P)L(Q) и
- [2].
Приложения
Маннила и Миик[14] использовали последовательно-параллельные частичные порядки в качестве модели последовательности событий в данных временного ряда. Они описали алгоритмы машинного обучения для моделей логического вывода для этого типа и продемонстрировали эффективность алгоритмов на выработке обязательных требований курса, исходя из регистрационных данных студентов, а также на моделировании шаблонов использования браузеров[6].
Амер с соавторами[15] утверждает, что последовательно-параллельные частичные порядки удобны для моделирования запросов последовательности передачи мультимедиа презентаций. Они использовали формулу для вычисления числа линейных продолжений последовательно-параллельного частичного порядка в качестве базиса анализа алгоритмов передачи мультимедиа[7].
Чаудхари с соавторами[16] использовал последовательно-параллельные частичные порядки для моделирования зависимостей задач в потоке данных массовой обработки данных для компьютерного зрения. Они показали, что при использовании последовательно-параллельных порядков для этой задачи можно эффективно построить оптимальное расписание, назначающее различные задачи различным процессорам параллельной вычислительной системы с целью оптимизировать пропускную способность системы[8].
Класс упорядочений, несколько более общий понятию последовательно-параллельных частичных порядков, задаётся PQ-деревьями, структурами данных, применяемых в алгоритмах для проверки, является ли граф планарным, и распознавания интервальных графов[17]. Узел P PQ-дерева допускает все возможные упорядочения его наследников подобно параллельному соединению в частичных порядках, в то время как узел Q требует следования наследников в фиксированном линейном порядке подобно последовательным частичным порядкам. Однако, в отличие от последовательно-параллельных частичных порядков, PQ-деревья позволяют обратить линейный порядок в любом узле Q.
Примечания
- Bechet, De Groote, Retoré, 1997, с. 230–240.
- Möhring, 1989, с. 105–194.
- Valdes, Tarjan, Lawler, 1982, с. 298–313.
- Jung, 1978, с. 125–133.
- Lawler, 1978, с. 75–90.
- Mannila, Meek, 2000, с. 161–168.
- Amer, Chassot, Connolly и др., 1994, с. 440–456.
- Choudhary, Narahari, Nicol, Simha, 1994, с. 439–445.
- Furnas, Zacks, 1994, с. 330–336.
- Гуров, 2012, с. 111 Определение 3.14.
- Кузнецов.
- Ma, Spinrad, 1991, с. 175–183.
- Brightwell, Winkler, 1991, с. 225–242.
- Mannila, Meek, 2000.
- Amer, Chassot, Connolly и др., 1994.
- Choudhary, Narahari, Nicol, Simha, 1994.
- Booth, Lueker, 1976, с. 335–379.
Литература
- Bechet D., De Groote P., Retoré C. A complete axiomatisation for the inclusion of series-parallel partial orders // Rewriting Techniques and Applications. — Springer-Verlag, 1997. — Т. 1232. — С. 230–240. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-62950-5_74.
- Möhring R. H. Computationally tractable classes of ordered sets // Algorithms and Order: Proceedings of the NATO Advanced Study Institute on Algorithms and Order, Ottawa, Canada, May 31-June 13, 1987. — Springer-Verlag, 1989. — Т. 255. — С. 105–194. — (NATO Science Series C). — ISBN 978-0-7923-0007-6.
- Valdes J., Tarjan R. E., Lawler E. L. The recognition of series parallel digraphs // SIAM Journal on Computing. — 1982. — Т. 11, вып. 2. — С. 298–313. — doi:10.1137/0211023.
- Lawler E. L. Sequencing jobs to minimize total weighted completion time subject to precedence constraints // Annals of Discrete Mathematics. — 1978. — Т. 2. — С. 75–90. — doi:10.1016/S0167-5060(08)70323-6.
- Jung H. A. On a class of posets and the corresponding comparability graphs // Journal of Combinatorial Theory, Series B. — 1978. — Т. 24, вып. 2. — С. 125–133. — doi:10.1016/0095-8956(78)90013-8.
- Furnas G. W., Zacks J. Multitrees: enriching and reusing hierarchical structure // Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94). — 1994. — С. 330–336. — doi:10.1145/191666.191778.
- Ma T.-H., Spinrad J. Transitive closure for restricted classes of partial orders // Order. — 1991. — Т. 8, вып. 2. — С. 175–183. — doi:10.1007/BF00383402.
- Brightwell G. R., Winkler P. Counting linear extensions // Order. — 1991. — Т. 8, вып. 3. — С. 225–242. — doi:10.1007/BF00383444.
- Amer P. D., Chassot C., Connolly T. J., Diaz M., Conrad P. Partial-order transport service for multimedia and other applications // IEEE/ACM Transactions on Networking. — 1994. — Т. 2, вып. 5. — С. 440–456. — doi:10.1109/90.336326.
- Choudhary A. N., Narahari B., Nicol D. M., Simha R. Optimal processor assignment for a class of pipelined computations // IEEE Transactions on Parallel and Distributed Systems. — 1994. — Т. 5, вып. 4. — С. 439–445. — doi:10.1109/71.273050.
- Booth K. S., Lueker G. S. Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms // Journal of Computer and System Sciences. — 1976. — Т. 13, вып. 3. — С. 335–379. — doi:10.1016/S0022-0000(76)80045-1.
- Mannila H. Meek C. Global partial orders from sequential data // Proc. 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2000). — 2000. — С. 161–168. — doi:10.1145/347090.347122.
- Кузнецов С.О. Теория решёток для интеллектуального анализа данных. (недоступная ссылка)
- Гуров С.И. Булевы алгебры, упорядоченные множества, решётки: определения, свойства, примеры. — М.: КРАСАНД, 2012. — ISBN 978-5-396-00456-6.