Транзитивное сокращение

В теории графов любое бинарное отношение R на X можно понимать как ориентированный граф (V, A), где V = X — это вершины и A = R — дуги графа. Транзитивное сокращение графа иногда называют минимальным представлением. Следующие рисунки представляют нетранзитивное отношение (слева) и его транзитивное сокращение (справа).

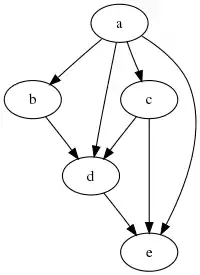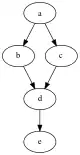Транзитивное сокращение конечного ориентированного ацикличного графа единственно.

Транзитивное сокращение ${\displaystyle R^{-}}$ отношения без циклов ${\displaystyle R}$ можно найти используя его транзитивное замыкание ${\displaystyle R^{+}}$:

${\displaystyle R^{-}=R-(R\circ R^{+})}$

Здесь ${\displaystyle \circ }$ означает композицию отношений.

Ахо, Гарей и Ульман (1972), введшие в обиход термин «транзитивное сокращение» в описываемом здесь смысле, установили также связь между транзитивным замыканием и сокращением:

• для определения транзитивного сокращения они расширили нахождение транзитивного замыкания обработкой циклов;
• они показали, как из транзитивного сокращения получить транзитивное замыкание;
• они показали, что нахождение транзитивного сокращения и замыкания имеют одну и ту же вычислительную сложность.

Утилита tred в Graphviz[1] осуществляет транзитивное сокращение графа, используя поиск в глубину.

Одной из самых хорошо изученных проблем в вычислительной теории графов является хранение последовательной истории транзитивных замыканий графа при вставке или удалении вершин и дуг. В 1987-м году Потре (J. A. La Poutré) и Жан ван Льювен (Jan van Leeuwen) описали в своем часто цитируемом труде Maintenance Of Transitive Closures And Transitive Reductions Of Graphs («Управление транзитивными замыканиями и сокращениями графа») алгоритм хранения истории как для замыкания, так и для сокращения графа.[2]

Алгоритм использует

O(|E_new||V|)

время для последовательной вставки дуг и

O(|E_old||V|+|E_old|²)

для последовательного удаления, где E_old — набор дуг перед вставкой или удалением и E_new — после. Для графов, в которых отсутствуют циклы, удаление требует только

O(|E_old||V|)

времени.

• Транзитивность

• A. Aho, M. Garey, J. Ullman. The Transitive Reduction of a Directed Graph (англ.) // SIAM Journal on Computing : journal. — 1972. — June (vol. 1, no. 2). — P. 131—137. — doi:10.1137/0201008.

• Mathworld: Transitive reduction
• Э.Рейнгольд, Ю.Нивергельт, Н.Део КОМБИНАТОРНЫЕ АЛГОРИТМЫ. ТЕОРИЯ И ПРАКТИКА М.: Мир, 1980, 476 стр.