Полная раскраска
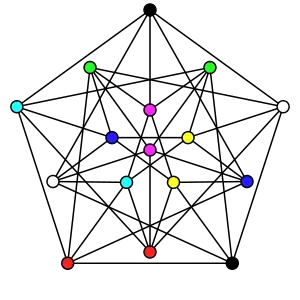
В теории графов полная раскраска — это противоположность гармонической раскраске в том смысле, что это раскраска вершин, в которой каждая пара цветов встречается по меньшей мере на одной паре смежных вершин. Эквивалентно, полная раскраска — это минимальная раскраска, в том смысле, что её нельзя преобразовать в правильную раскраску с меньшим числом цветов путём слияния двух цветов. Ахроматическое число ψ(G) графа G — это максимальное число цветов среди всех полных раскрасок графа G.
Теория сложности
Нахождение ψ(G) является задачей оптимизации. Проблема разрешимости для полной раскраски может быть сформулирована как:
- ДАНО: Граф и положительное целое число
- ВОПРОС: Существует ли разбиение множества вершин на или более непересекающихся множеств таких, что каждое является независимым множеством для и таких, что для каждой пары различных множеств независимым множеством не является.
Определение ахроматического числа является NP-трудной. Определение, не будет ли ахроматическое число больше заданного числа является NP-полной, как показали Янакакис и Гаврил (Yannakakis, Gavril) в 1978 году путём преобразования из задачи поиска минимального наибольшего паросочетания[1].
Заметим, что любая раскраска графа с минимальным числом цветов должна быть полной раскраской, так что минимизация числа цветов полной раскраски является просто переформулировкой стандартной задачи раскраски графа.
Алгоритм
Оптимизационная задача допускает аппроксимацию с гарантированной эффективностью [2].
Специальные случаи графов
Задача определения ахроматического числа остаётся NP-полной также для некоторых специальных классов графов: двудольные графы[3], дополнения двудольных графов (то есть, графы, не имеющие независимого множества с более чем двумя вершинами)[1], кографы, интервальные графы[4] и даже деревья[5].
Для дополнений деревьев ахроматическое число может быть вычислено за полиномиальное время[6]. Для деревьев можно задачу аппроксимировать с постоянным коэффициентом[2].
Известно, что ахроматическое число n-мерного графа гиперкуба пропорционально , но точная константа пропорциональности не известна[7].
Примечания
- Michael R. Garey and David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W. H. Freeman, 1979. — ISBN 0-7167-1045-5. A1.1: GT5, pg. 191.
- Amitabh Chaudhary, Sundar Vishwanathan. Approximation algorithms for the achromatic number // Journal of Algorithms. — 2001. — Т. 41, вып. 2. — С. 404—416. — doi:10.1006/jagm.2001.1192..
- M. Farber, G. Hahn, P. Hell, D. J. Miller. Concerning the achromatic number of graphs // Journal of Combinatorial Theory, Series B. — 1986. — Т. 40, вып. 1. — С. 21—39. — doi:10.1016/0095-8956(86)90062-6..
- H. Bodlaender. Achromatic number is NP-complete for cographs and interval graphs // Inform. Proc. Lett.. — 1989. — Т. 31, вып. 3. — С. 135—138. — doi:10.1016/0020-0190(89)90221-4..
- D. Manlove, C. McDiarmid. The complexity of harmonious coloring for trees // Discrete Applied Mathematics. — 1995. — Т. 57, вып. 2-3. — С. 133—144. — doi:10.1016/0166-218X(94)00100-R..
- M. Yannakakis, F. Gavril. Edge dominating sets in graphs // SIAM Journal on Applied Mathematics. — Т. 38, вып. 3. — С. 364—372. — doi:10.1137/0138030..
- Y. Roichman. On the Achromatic Number of Hypercubes // Journal of Combinatorial Theory, Series B. — 2000. — Т. 79, вып. 2. — С. 177—182. — doi:10.1006/jctb.2000.1955..
