Поверхности постоянной средней кривизны
Поверхности постоянной средней кривизны — класс поверхностей моделирующий поверхности мыльных плёнок разделяющие области с фиксированной разницей давлений. В частном случае, если давление с обеих сторон равно, модель определяет минимальные поверхности.
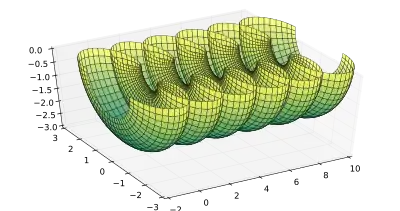
Нодоид, поверхность с постоянной средней кривизной
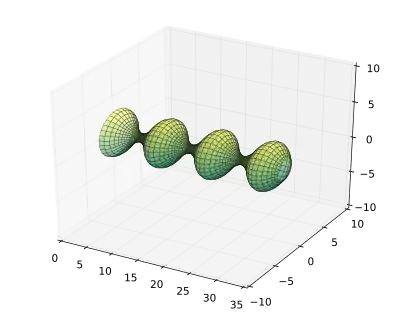
Ундулоид, поверхность с постоянной средней кривизной
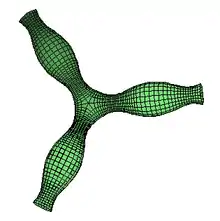
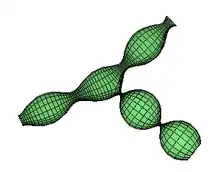
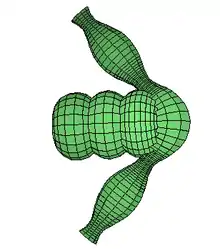
Определяются как гладкие поверхности с постоянной средней кривизной.
История исследования
- В 1841 году Шарль-Эжен Делоне доказал, что единственными поверхностями вращения с постоянной средней кривизной были поверхности, полученные вращением кривых получаемых качением коник. Таковыми являются плоскость, цилиндр, сфера, катеноид, ундулоид и нодоид.[1]
- В 1853 году Дж. Джелле показал, что если компактная звёздчатая поверхность в с постоянной средней кривизной, то это стандартная сфера.[2] Впоследствии Александр Данилович Александров доказал, что компактная вложенная поверхность в с постоянной средней кривизной должна быть сфера.[3]
- На основании этого Хайнц Хопф в 1956 году предположил, что любая погружённая компактная ориентируемая гиперповерхность постоянной средней кривизны в должна быть круглой сферой.
- Это предположение было опровергнуто в 1982 году Ву-И Сяном с использованием контрпримера в .
- В 1984 году Генри К. Венте построил так называемый тор Венте — погружение в тора постоянной средней кривизны.[4]
Приложения
Помимо мыльных плёнок, поверхности постоянной средней кривизны появляются как границы раздела газ-жидкость на супергидрофобной поверхности.[11]
В архитектуре поверхности постоянной средней кривизны используются в конструкциях с воздушной опорой, таких, как надувные купола и ограждения, а также в качестве источника плавных органических форм.[12]
Примечания
- C. Delaunay, Sur la surface de révolution dont la courbure moyenne est constante, J. Math. Pures Appl., 6 (1841), 309—320.
- J. H. Jellet, Sur la Surface dont la Courbure Moyenne est Constant, J. Math. Pures Appl., 18 (1853), 163—167
- A. D. Alexandrov, Uniqueness theorem for surfaces in the large, V. Vestnik, Leningrad Univ. 13, 19 (1958), 5-8, Amer. Math. Soc. Trans. (Series 2) 21, 412—416.
- Wente, Henry C. (1986), Counterexample to a conjecture of H. Hopf., Pacific Journal of Mathematics Т. 121: 193–243, doi:10.2140/pjm.1986.121.193, <http://projecteuclid.org/euclid.pjm/1102702809>.
- Karsten Grosse-Brauckmann, Robert B. Kusner, John M. Sullivan. Coplanar constant mean curvature surfaces. Comm. Anal. Geom. 15:5 (2008) pp. 985—1023. ArXiv math.DG/0509210.
- N. Kapouleas. Complete constant mean curvature surfaces in Euclidean three space, Ann. of. Math. (2) 131 (1990), 239—330
- Rafe Mazzeo, Daniel Pollack, Gluing and Moduli for Noncompact Geometric Problems. 1996 arXiv: dg-ga/9601008
- I. Sterling and H. C. Wente, Existence and classification of constant mean curvature multibubbletons of finite and infinite type, Indiana Univ. Math. J. 42 (1993), no. 4, 1239—1266.
- Meeks W. H., The topology and geometry of embedded surfaces of constant mean curvature, J. Diff. Geom. 27 (1988) 539—552.
- Korevaar N., Kusner R., Solomon B., The structure of complete embedded surfaces with constant mean curvature, J. Diff. Geom. 30 (1989) 465—503.
- E.J. Lobaton, T.R. Salamon. Computation of constant mean curvature surfaces: Application to the gas-liquid interface of a pressurized fluid on a superhydrophobic surface. Journal of Colloid and Interface Science. Volume 314, Issue 1, 1 October 2007, Pages 184—198
- Helmut Pottmann, Yang Liu, Johannes Wallner, Alexander Bobenko, Wenping Wang. Geometry of Multi-layer Freeform Structures for Architecture. ACM Transactions on Graphics — Proceedings of ACM SIGGRAPH 2007 Volume 26 Issue 3, July 2007 Article No. 65
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.