Нодоид

Нодоид — пример поверхности постоянной средней кривизны. Является также поверхностью вращения.

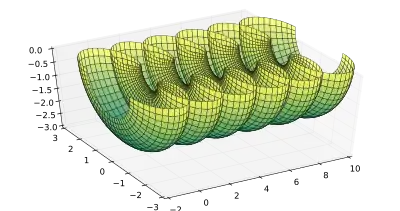
Половинка нодоида.

В 1841 году Шарль Делоне доказал, что единственными вращающимися поверхностями с постоянной средней кривизной были поверхности, полученные вращением коник. Это плоскость, цилиндр, сфера, катеноид, ундулоид и нодоид.[1]

Построение

Сначала строится кривая путем катания гиперболы по оси и отслеживания её фокуса. Далее берётся поверхностью вращения полученной кривой вокруг оси.[2]

Примечания

C. Delaunay, Sur la surface de révolution dont la courbure moyenne est constante, J. Math. Pures Appl., 6 (1841), 309–320.
Oprea, John (2007), Differential Geometry and its Applications (2nd ed.), Classroom Resource Materials Series, Washington, DC: Mathematical Association of America, с. 147–148, ISBN 978-0-88385-748-9.

Ссылки

Нодоид // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] C. Delaunay, Sur la surface de révolution dont la courbure moyenne est constante, J. Math. Pures Appl., 6 (1841), 309–320.

[2] Oprea, John (2007), Differential Geometry and its Applications (2nd ed.), Classroom Resource Materials Series, Washington, DC: Mathematical Association of America, с. 147–148, ISBN 978-0-88385-748-9.