Парадокс Линдли

Частотный подход проверки ${\displaystyle H_{0}}$ заключается в вычислении p-значения, вероятности наблюдения доли мальчиков не менее ${\displaystyle x}$ в предположении, что гипотеза ${\displaystyle H_{0}}$ верна. Поскольку число рождений большое, мы можем использовать нормальную аппроксимацию для доли рождения мальчиков ${\displaystyle X\sim N(\mu ,\sigma ^{2})}$, с ${\displaystyle \mu =np=n\theta =98451\times 0,5=49225,5}$ и ${\displaystyle \sigma ^{2}=n\theta (1-\theta )=98451\times 0,5\times 0,5=24612,75}$ для вычисления

${\displaystyle {\begin{aligned}P(X\geq x\mid \mu =49225,5)=\int _{x=49581}^{98451}{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-({\frac {u-\mu }{\sigma }})^{2}/2}du\\=\int _{x=49581}^{98451}{\frac {1}{\sqrt {2\pi (24612,75)}}}e^{-{\frac {(u-49225,5)^{2}}{24612,75}}/2}du\approx 0,0117.\end{aligned}}}$

Мы также будем удивлены, если рассмотрим рождение 48870 девочек, то есть ${\displaystyle x\approx 0,4964}$, так что частотный тест обычно осуществаляет двухстороннюю проверку, для которой p-значение было бы ${\displaystyle p\approx 2\times 0,0117=0,0235}$. В обоих случаях p-значение меньше уровня значимости ${\displaystyle \alpha }$ в 5%, так что частотный подход отвергает гипотезу ${\displaystyle H_{0}}$ как несогласующуюся с наблюдаемыми данными.

Предполагая, что нет причин для предпочтения одной гипотезы другой, байесовский подход заключается в назначении априорных вероятностей ${\displaystyle \pi (H_{0})=\pi (H_{1})=0,5}$, однородного распределения для ${\displaystyle \theta }$ для гипотезы ${\displaystyle H_{1}}$ и, затем, вычисления апостериорной вероятности для ${\displaystyle H_{0}}$ с помощью теоремы Байеса,

${\displaystyle P(H_{0}\mid k)={\frac {P(k\mid H_{0})\pi (H_{0})}{P(k\mid H_{0})\pi (H_{0})+P(k\mid H_{1})\pi (H_{1})}}.}$

После наблюдения рождения ${\displaystyle k=49581}$ мальчиков из ${\displaystyle n=98451}$ новорождённых мы можем вычислить апостериорную вероятность каждой гипотезы с помощью функции распределения масс для биномиальной переменной,

${\displaystyle {\begin{aligned}P(k\mid H_{0})&={n \choose k}(0,5)^{k}(1-0,5)^{n-k}\approx 1,95\times 10^{-4}\\P(k\mid H_{1})&=\int _{0}^{1}{n \choose k}\theta ^{k}(1-\theta )^{n-k}d\theta ={n \choose k}\mathrm {\mathrm {B} } (k+1,n-k+1)=1/(n+1)\approx 1,02\times 10^{-5}\end{aligned}}}$

где ${\displaystyle \mathrm {\mathrm {B} } (a,b)}$ является бета-функцией.

Из этих значений мы находим апостериорную вероятность ${\displaystyle P(H_{0}\mid k)\approx 0,95}$, которая строго предпочитает ${\displaystyle H_{0}}$ перед ${\displaystyle H_{1}}$.

Два подхода, частотный и байесовский, оказываются в конфликте, а это и есть «парадокс».

Однако, по меньшей мере, в примере Линдли, если мы возьмём последовательность уровней значимости ${\displaystyle \alpha _{n}}$, таких, что ${\displaystyle \alpha _{n}=n^{-k}}$ с ${\displaystyle k>{\tfrac {1}{2}}}$, то апостериорная вероятность нулевой гипотезы стремится к 0, что согласуется с отказом от нулевой гипотезы[3]. В нашем числовом примере, если принять ${\displaystyle k>{\tfrac {1}{2}}}$, в результате получим уровень значимости 0,00318, так что частотный подход не будет отбрасывать нулевую гипотезу, которая в общих чертах согласуется с байесовским подходом.

Распределение p при нулевой гипотезе и апостериорное распределение p.

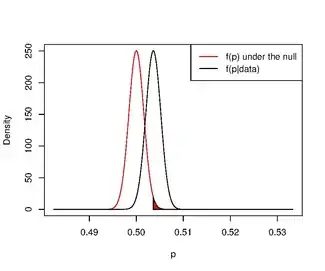
Если используется информативное априорное распределение и проверка гипотезы, более похожей на гипотезу в частотном подходе, парадокс исчезает.

Например, если мы вычисляем апостериорное распределение ${\displaystyle P(\theta \mid x,n)}$, используя однородное априорное распределение с ${\displaystyle \theta }$ (то есть ${\displaystyle \pi (\theta \in [0,1])=1}$), мы получим

${\displaystyle P(\theta \mid k,n)=\mathrm {\mathrm {B} } (k+1,n-k+1).}$

Если мы используем это для проверки вероятности, что новорождённый более вероятно будет мальчиком, чем девочкой, то есть ${\displaystyle P(\theta >0,5\mid k,n)}$, мы получим:

${\displaystyle \int _{0,5}^{1}\mathrm {\mathrm {B} } (49582,48871)\approx 0,983.}$

Другими словами, очень похоже, что пропорция рождения мальчиков выше 0,5.

Ни один из анализов не даёт оценку величины эффекта прямо, но оба могут быть использованы для определения, например, является ли доля рождений мальчиков выше некоторого определённого порога.

Явное расхождение между двумя подходами вызвано комбинацией факторов. Во-первых, частотный подход проверяет ${\displaystyle H_{0}}$ выше без учёта ${\displaystyle H_{1}}$. Байесовский подход вычисляет ${\displaystyle H_{0}}$ как альтернативу к ${\displaystyle H_{1}}$ и находит, что первая гипотеза больше согласуется с наблюдениями. Это потому, что последняя гипотеза существенно более размыта, так как значение ${\displaystyle \theta }$ может быть любым в интервале ${\displaystyle [0,1]}$, что приводит к очень низкой апостериорной вероятности. Чтобы понять, почему, полезно рассмотреть две гипотезы как генераторы наблюдений:

• В гипотезе ${\displaystyle H_{0}}$ мы выбираем ${\displaystyle \theta \approx 0,500}$ и задаём вопрос, насколько правдоподобно видеть 49581 мальчика при 98451 новорождённом.
• В гипотезе ${\displaystyle H_{1}}$ мы выбираем ${\displaystyle \theta }$ случайно между 0 и 1 и задаём тот же вопрос.

Большинство возможных значений для ${\displaystyle \theta }$ при гипотезе ${\displaystyle H_{1}}$ очень плохо поддерживаются наблюдениями. По существу, явное несогласие между методами вообще не является несогласием, а являются двумя различными утверждениями относительно данных:

• Частотный подход находит, что ${\displaystyle H_{0}}$ плохо объясняется наблюдениями.
• Байесовский подход находит, что гипотеза ${\displaystyle H_{0}}$ существенно лучше объясняется наблюдениями, чем гипотеза ${\displaystyle H_{1}}$.

Отношение пола новорождённых в 50/50 (мальчиков/девочек) согласно частотному тесту неправдоподобно. Всё же отношение 50/50 является лучшим приближением, чем большинство, но не все другие отношения. Гипотеза ${\displaystyle \theta \approx 0,504}$ подходила бы наблюдениям много лучше, чем все другие отношения, включая ${\displaystyle \theta \approx 0,500}$.

Например[5], из этого выбора гипотезы и априорной вероятности следует утверждение: «Если ${\displaystyle \theta }$ > 0,49 и ${\displaystyle \theta }$ < 0,51, то априорная вероятность ${\displaystyle \theta }$ быть ровно 0,5 равна 0,50/0,51 ${\displaystyle \approx }$ 98 %». Если дано такое сильное предпочтение для ${\displaystyle \theta =0,5}$, легко видеть, что байесовский подход высказывается в пользу ${\displaystyle H_{0}}$, учитывая, что ${\displaystyle x\approx 0,5036}$, даже когда наблюдаемое значение ${\displaystyle x}$ лежит в ${\displaystyle 2,28\sigma }$ от 0,5. Отклонение более ${\displaystyle 2\sigma }$ от ${\displaystyle H_{0}}$ считается значимым в частотном подходе, но значимость отклоняется априорной вероятностью в байесовском подходе.

Если смотреть в другую сторону, мы можем видеть, что априорное распределение существенно плоским с дельта-функцией в точке ${\displaystyle \theta =0,5}$. Ясно, что является сомнительным. Фактически, если вы попробуете нарисовать вещественные числа как непрерывные, будет логично предположить, что невозможно для заданного параметра ${\displaystyle P(\theta =0,5)=0}$.

Более реалистичное распределение для ${\displaystyle \theta }$ на альтернативной гипотезе даёт менее удивительные результаты для апостериорной вероятности гипотезы ${\displaystyle H_{0}}$. Например, если мы заменим ${\displaystyle H_{1}}$ на ${\displaystyle H_{2}:\theta =x}$, то есть оценку максимального правдоподобия для ${\displaystyle \theta }$, апостериорная вероятность гипотезы ${\displaystyle H_{0}}$ будет только 0,07 по сравнению с 0,93 для гипотезы ${\displaystyle H_{2}}$ (конечно, нельзя использовать в действительности оценку максимального правдоподобия как часть априорного распределения).