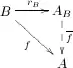Отражающая подкатегория

В математике, подкатегория A категории B называется отражающей, если функтор вложения A в B имеет левый сопряженный. Этот сопряженный функтор часто называют отражателем. Двойственное определение — A ко-отражающая , если функтор вложения имеет правый сопряженный.

Явное определение

Подкатегория A категории B называется отражающей в B, если для каждого объекта B категории B существует объект $A_{B}$ категории A и B-морфизм $r_{B}\colon B\to A_{B}$ , такой что для любого B-морфизма $f\colon B\to A$ существует единственный A-морфизм ${\overline {f}}\colon A_{B}\to A$ , такой что ${\overline {f}}\circ r_{B}=f$ :

Пара $(A_{B},r_{B})$ называется A-отражателем B. Морфизм $r_{B}$ называется A-отражающей стрелкой.

Примеры

Алгебра

Категория абелевых групп Ab — отражающая подкатегория категории групп Grp. Отражатель — функтор, отправляющий каждую группу в её абелианизацию. В свою очередь, категория групп — отражающая подкатегория категории полугрупп с делением.
Категория полей — отражающая подкатегория категории целостных колец (с инъективными гомоморфизмами колец). Отражатель — функтор, отправляющий кольцо в его поле частных.
Категория абелевых групп кручения — ко-отражающая подкатегория категории абелевых групп. Отражатель отправляет абелеву группу в её подгруппу кручения.
Категория векторных пространств над данным полем k — это отражающая подкатегория категории множеств. Отражатель — функтор, отправляющий множество B в свободное векторное пространство, порожденное элементами B над k.

Топология

Колмогоровские пространства (T₀-пространства) — отражающая подкатегория Top, категории топологических пространств, и колмогоровский фактор является отражателем.
Категория компактных хаусдорфовых — отражающая подкатегория топологических пространств с аксиомой Тихонова. Отражатель — Компактификация Стоуна — Чеха.
Категория полных метрических пространствs c равномерно непрерывными отображениями — отражающая полная подкатегория категории метрических пространств. Отражатель — пополнение метрического пространства.

Функциональный анализ

Категория банаховых пространств — отражающая полная подкатегория категории нормированных пространств и ограниченных линейных операторов. Отражатель — пополнение по норме.

Примечания

Adámek, Jiří; Horst Herrlich, George E. Strecker. Abstract and Concrete Categories (неопр.). — New York: John Wiley & Sons, 1990.
Peter Freyd, Andre Scedrov. Categories, Allegories (неопр.). — North-Holland, 1990. — (Mathematical Library Vol 39). — ISBN 978-0-444-70368-2.
Herrlich, Horst. Topologische Reflexionen und Coreflexionen (неопр.). — Berlin: Springer, 1968.
Mark V. Lawson. Inverse semigroups: the theory of partial symmetries (англ.). — World Scientific, 1998. — ISBN 978-981-02-3316-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.