Многочлены Бернулли
В математике Многочле́ны Берну́лли — многочлены, названные в честь Якоба Бернулли, возникающие при изучении многих специальных функций, в частности ζ-функции Римана и ζ-функции Гурвица, также являются частным случаем последовательности Аппеля. В отличие от ортогональных многочленов, многочлены Бернулли замечательны тем, что число корней в интервале не увеличивается с увеличением степени многочлена. При неограниченном увеличении степени многочлены Бернулли приближаются к тригонометрическим функциям.
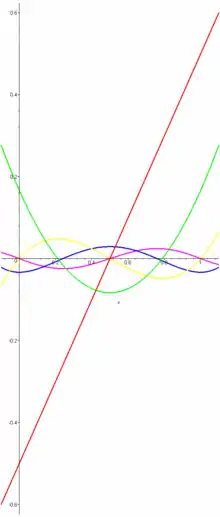
Определение
Многочлены Бернулли можно определить различными способами. Выбор определения зависит от удобства в том или ином случае.
Представление дифференциальным оператором
Явное выражение для небольших степеней
Несколькими первыми многочленами Бернулли являются:
Свойства
Начальные значения
начальные значения многочленов Бернулли при равны соответствующим числам Бернулли:
- .
Дифференцирование и интегрирование
Вычисляя производную от производящей функции:
- .
Левая часть отличается от производящей функции только множителем , поэтому
- .
Сравнивая коэффициенты при одинаковых степенях , получаем:
- , откуда
- . (функции, удовлетворяющие подобному свойству называются последовательностью Аппеля).
Из последнего равенства следует правило интегрирования многочленов Бернулли:
- .
Также бывает полезно свойство сбалансированности:
- (при )
Теорема об умножении аргумента
Пусть m — произвольное натуральное число, тогда
Из построенных разложений следует теорема об умножении аргумента:
- .