Метод Хука — Дживса
Метод Хука — Дживса (англ. Hooke — Jeeves, Pattern search), также известный как метод конфигураций — как и алгоритм Нелдера — Мида, служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две фазы: исследующий поиск и поиск по образцу.
На начальном этапе задаётся стартовая точка (обозначим её 1) и шаги hi по координатам. Затем замораживаем значения всех координат кроме 1-й, вычисляем значения функции в точках x0+h0 и x0-h0 (где x0 — первая координата точки, а h0 — соответственно значение шага по этой координате) и переходим в точку с наименьшим значением функции. В этой точке замораживаем значения всех координат кроме 2-й, вычисляем значения функции в точках x1+h1 и x1-h1, переходим в точку с наименьшим значением функции и т. д. для всех координат. В случае, если для какой-нибудь координаты значение в исходной точке меньше, чем значения для обоих направлений шага, то шаг по этой координате уменьшается. Когда шаги по всем координатам hi станут меньше соответствующих значений ei, алгоритм завершается, и точка 1 признаётся точкой минимума.
Иллюстрация первого этапа для двух координат:
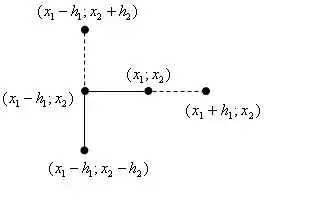
Таким образом, проведя исследующий поиск по всем координатам, мы получим новую точку с наименьшим значением функции в окрестности (обозначим её 2). Теперь можно осуществлять переход ко 2 фазе алгоритма.
На этапе поиска по образцу откладывается точка 3 в направлении от 1 к 2 на том же расстоянии. Её координаты получаются по формуле , где xi — точка с номером i, λ — параметр алгоритма, обычно выбирающийся равным 2. Затем в новой точке 3 проводится исследующий поиск, как на 1 фазе алгоритма, за исключением того, что шаг на этой фазе не уменьшается. Если на этой фазе в результате исследующего поиска удалось получить точку 4, отличную от точки 3, то точку 2 переобозначим на 1, а 4 на 2 и повторим поиск по образцу. В случае если не удаётся найти точку 4, отличную от точки 3, то точку 2 переобозначим на точку 1 и повторим 1-ю фазу алгоритма — исследующий поиск.
Иллюстрация второго этапа для двух координат:
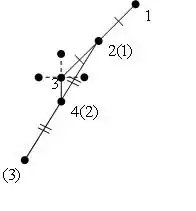
В скобках отмечены имена точек после переобозначения. На иллюстрации хорошо заметно, как алгоритм корректирует своё направление в зависимости от найденных значений функции.
Литература
- Р. Хук , Т. А. Дживс «Прямой поиск решения для числовых и статических проблем», 212—219 с., 1961.
- C. T. Kelley. Iterative methods for optimization, 180 p
Ссылки
- https://web.archive.org/web/20120905151449/http://www.theweman.info/topics/t4r5part1.html
- Методы многомерное оптимизации в Интуит.ру.
- А.В. Аттетков, С.В. Галкин, В.С. Зарубин. Метод Хука - Дживса // Методы оптимизации. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. — С. 285. — 440 с. — (Математика в техническом университете; Вып. XIV). (недоступная ссылка)