Лемма Веррьера
Лемма Веррьера — теорема в геометрии треугольника, связанная со свойствами описанной и полувписанной окружностей треугольника.
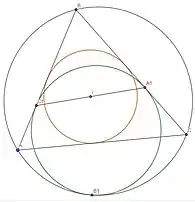
Формулировка
Если окружность ω касается сторон AB,BC и дуги AC описанной окружности треугольника ABC, соответственно в точках C1,A1,B1, то точки C1,I,A1,где I — инцентр треугольника ABC, коллинеарны.
Доказательство
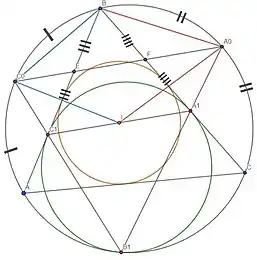
Заметим, что по лемме Архимеда прямая B1A1 проходит через середину дуги BC описанной окружности, не содержащей точку A . Аналогично, прямая B1C1 проходит через середину дуги AB, не содержащей вершину C. Обозначим середины этих дуг через A0, C0 соответственно. Из той же леммы Архимеда следует, что A0B2 = A0A1 · A0B. Следовательно, степень точки A0 одинакова относительно окружности ω и точки B. Аналогичное утверждение верно и для точки C0. Из этого следует, что прямая A0C0 — радикальная ось точки B и окружности ω. Поэтому прямая A0C0 проходит через середины отрезков BA1,BC1. Значит, прямая A0C0 содержит среднюю линию FE треугольника C1BA1. Следовательно, образ точки B, при отражении точки B относительно прямой A0C0, лежит на прямой A1C1.
С другой стороны, по лемме о трезубце IC0 = BC0 и IA0 = BA0. Поэтому точка B при отражении относительно прямой A0C0 переходит в точку I. Откуда и следует, что точка I лежит на прямой A1C1.
Замечание
Окружность ω называют полувписанной окружностью треугольника ABC
Примечания
- П. А. Кожевников «Полувписанная» окружность https://geometry.ru/persons/kozhevnikov/poluvpis.pdf
- Экзаменационная работа А. Гаркового по геометрии на тему «Полувписанная окружность» https://www.mccme.ru/circles/oim/mmks/works/garkavyi.pdf
