Криптография на решётках
Криптография на решётках — подход к построению алгоритмов асимметричного шифрования с использованием задач теории решёток, то есть задач оптимизации на дискретных аддитивных подгруппах, заданных на множестве .
Наряду с другими методами постквантовой криптографии, считается перспективным в связи с возможностями квантового компьютера взламывать широко используемые асимметричные системы шифрования, основанные на двух типах задач теории чисел: задачах факторизации целых чисел и задачах дискретного логарифмирования. Сложность взлома алгоритмов, построенных на решётках, крайне велика, самые лучшие алгоритмы могут решить эту задачу с трудом за экспоненциальное время. По состоянию на середину 2010-х годов неизвестно ни одного квантового алгоритма, способного справиться лучше обычного компьютера.
Предпосылки создания
В 1995 году Питер Шор продемонстрировал полиномиальный алгоритм для взлома криптографических систем с открытым ключом при использовании квантового компьютера, тем самым определив период существования данных систем до возникновения квантовых вычислителей достаточной размерности.
В 1996 году Лов Гровер продемонстрировал общий метод поиска в базе данных позволяющий производить расшифровку симметричных алгоритмов шифрования, эквивалентную двукратному уменьшению ключа шифра.
В 2001 году группа специалистов IBM продемонстрировала выполнение алгоритма факторизации Шора для числа 15. Число было разложено на множители 3 и 5 при помощи квантового компьютера с 7 кубитами, построенного из 1810 молекул, состоящих из пяти атомов фтора и двух атомов углерода, с записью информации посредством радиосигналов и считыванием методами ядерного магнитного резонанса[1].
Начиная со второй половины 1990-х годов возникла необходимость поиска криптостойких к квантовым компьютерам задач для постквантовой эпохи шифрования, в качестве одного из подходов было предложено использовать решётки в — дискретные подгруппы вещественного векторного пространства, линейные оболочки которых совпадают с ним:
Вычислительно сложные задачи
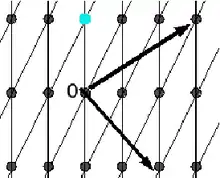
Задача нахождения кратчайшего вектора (SVP, англ. Shortest Vector Problem) — найти в заданном базисе решётки ненулевой вектор по отношению к определённой нормали[2].
Задача нахождения (приблизительно) идеального кратчайшего вектора (ISVP, англ. (approximate) ideal shortest vector problem) не считается NP-сложной. Однако, нет известных решёток, основанных на методе редукции, значительно более эффективных на идеальных структурах, чем на общих[3].
Ещё одна задача — нахождение (приблизительно) кратчайшего независимого вектора (SIVP, англ. (approximate) shortest independent vectors problem), в которой дан базис решётки и требуется найти линейно независимых векторов[4].
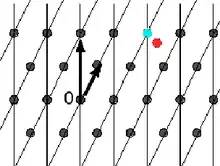
Задача нахождения ближайшего вектора (CVP, англ. Closest Vector Problem) — нахождение вектора в решётке по заданному базису и некоторому вектору, не принадлежащему решётке, при этом максимально схожего по длине с заданным вектором.
LLL-алгоритм
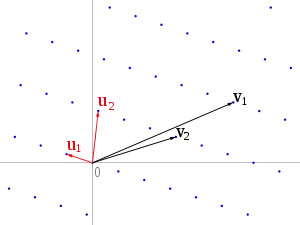
Все эти задачи разрешимы за полиномиальное время с помощью известного LLL-алгоритма изобретённого в 1982 году Арьеном Ленстрой, Хендриком Ленстрой и Ласло Ловасом[5].
В заданном базисе , с n-мерными целыми координатами, в решётке из , где , LLL-алгоритм находит более короткий (промерно[уточнить]) ортогональный базис за время:
- ,
где — это максимальная длина вектора в этом пространстве.
Основные криптографические конструкции и их стойкость
Шифрование
GGH — криптосистема основанная на CVP, а именно на односторонней функции с потайным входом опирающуюся на сложность редукции решётки. Была опубликована в 1997 году. Зная базис, можно сгенерировать вектор близкий к заданной точке, но зная это вектор нам необходим исходный базис, чтобы найти исходную точку. Алгоритм был проверен в 1999 году.
Реализация GGH
GGH состоит из открытого и секретного ключа.
Секретный ключ — это базис решётки и унимодулярная матрица .
Открытый ключ — некоторый базис в решётке в виде .
Для некоторого , пространство сообщения состоит из вектора , где .
Шифрование
Задано сообщение , искажение , открытый ключ :
В матричном виде:
- .
состоит из целых значений, точка решётки, и v также точка решётки. Тогда шифротекст:
Расшифрование
Для расшифрования необходимо вычислить:
Часть убирается, из соображений приближения. Сообщение:
Пример
Выберем решётку с базисом :
- and
где
- и
В результате:
Пусть сообщение и вектор ошибки . Тогда шифротекст:
- .
Для расшифровки необходимо вычислить:
- .
Округление даёт , восстановим сообщение:
- .
NTRUEncrypt — криптосистема основанная на SVP, является альтернативой RSA и ECC. В вычислении используется кольцо многочленов.
Подпись
Схема подписи GGH впервые предложена 1995 году и опубликована в 1997 году Голдрихом, основана на сложности нахождения ближайшего вектора. Идея заключалась в использовании решёток, для которых «плохой» базис, векторы длинные и почти параллельные, является открытым и «хороший» базис с короткими и почти ортогональными векторами, является закрытым. По их методу, сообщение необходимо хешировать в пространство, натянутое на решётку, а подпись для данного хэша в этом пространстве является ближайшим узлом решётки. Схема не имела формального доказательства безопасности, и её базовый вариант был взломан в 1999 году Нгуэном (Nguyen). В 2006 году модифицированная версия была снова взломана Нгуэном и Реджевом (Regev).
NTRUSign — специальная, более эффективная версия подписи GGH, отличающаяся меньшим ключом и размером подписи. Она использует только решётки подмножества множества всех решёток, связанных с некоторыми полиномиальными кольцами. NTRUSign была предложена на рассмотрение в качестве стандарта IEEE P1363.1.
Примечания
- Vandersypen, Lieven M. K.; Steffen, Matthias; Breyta, Gregory & Yannoni, Costantino S. (2001), Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance, Nature Т. 414 (6866): 883–887, PMID 11780055, doi:10.1038/414883a, <http://cryptome.org/shor-nature.pdf>
- [www.cs.elte.hu/~lovasz/scans/lll.pdf Factoring polynomials with rational coefficients], <www.cs.elte.hu/~lovasz/scans/lll.pdf>
- Generalized compact knapsacks are collision resistant. In:International colloquium on automata, languages and programming, <https://link.springer.com/content/pdf/10.1007/11787006.pdf>
- Complexity of lattice problems: a cryptographic perspective. The Kluwer international series in engineering and computer science, <http://cseweb.ucsd.edu/~daniele/papers/book.bib>
- Lenstra, A. K.; Lenstra, H. W., Jr.; Lovász, L. Factoring polynomials with rational coefficients (неопр.) // Mathematische Annalen. — 1982. — Т. 261, № 4. — С. 515—534. — doi:10.1007/BF01457454.