Кривая Евдокса
Кривая Евдокса (греческий: καμπύλη [γραμμή], что переводится как «кривая [линия]») — это кривая с уравнением в декартовых координатах
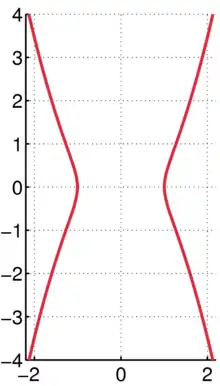
График кривой Евдокса с a = 1
из которого исключается решение x = y = 0.
Альтернативные параметризации
В полярной системе координат кривая Евдокса имеет уравнение
Эквивалентно, кривая имеет параметрическое представление
История
Эту кривую четвёртой степени изучал греческий астроном и математик Евдокс Книдский (408—347 до нашей эры) в связи с классической задачей удвоения куба.
Свойства
Кривая Евдокса симметрична как относительно оси x, так и оси y. Она пересекает ось x в точках (±a,0). Кривая имеет точки перегиба
(четыре точки перегиба, по одной в каждом квадранте). Верхняя половина кривой асимптотически приближается к при , и, фактически, можно записать
где
является -м числом Каталана.
Примечания
Литература
- J. Dennis Lawrence. A catalog of special plane curves. — Dover Publications, 1972. — С. 141–142. — ISBN 0-486-60288-5.
Ссылки
- O'Connor, John J.; Robertson, Edmund F., "Kampyle of Eudoxus", MacTutor History of Mathematics archive, University of St Andrews.
- Weisstein, Eric W. Kampyle of Eudoxus (англ.) на сайте Wolfram MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.