Координаты Эддингтона — Финкельштейна

Решение Шварцшильда в координатах Шварцшильда с подавленными двумя пространственными измерениями, то есть в зависимости только от времени t и расстояния от центра r. Красным цветом показаны направленные внутрь нулевые геодезические, синим — уходяие на бесконечность нулевые геодезические, зелёным (для двух других координат) — световые конусы, по которым движется свет, а массивные объекты движутся внутри конусов.

Координатами Шварцшильда называют координаты ${\displaystyle (t,r,\theta ,\varphi )}$, такие, что в этих координатах метрика Шварцшильда записывается в виде:

${\displaystyle ds^{2}=-\left(1-{\frac {2GM}{r}}\right)\,dt^{2}+\left(1-{\frac {2GM}{r}}\right)^{-1}\,dr^{2}+r^{2}d\Omega ^{2}}$

где

${\displaystyle d\Omega ^{2}\equiv d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}}$

стандартная риманова метрика двумерной сферы.

Здесь используются следующие условные обозначения: сигнатура метрики (− + + +) и натуральные единицы, где c = 1 — безразмерная скорость света, G — гравитационная постоянная, а M — характеристическая масса геометрии Шварцшильда.

Координаты Эддингтона — Финкельштейна основаны на черепашьей координате[4], которая происходит от одного из парадоксов Зенона Элейского о воображаемой гонке между «быстроногими» Ахиллесом и черепахой.

Черепашья координата ${\displaystyle r^{*}}$ определяется так[4]:

${\displaystyle r^{*}=r+2GM\ln \left|{\frac {r}{2GM}}-1\right|\,,}$

которая удовлетворяет:

${\displaystyle {\frac {dr^{*}}{dr}}=\left(1-{\frac {2GM}{r}}\right)^{-1}\,.}$

Черепашья координата ${\displaystyle r^{*}}$ приближается к ${\displaystyle -\infty }$, когда ${\displaystyle r}$ приближается к радиусу Шварцшильда ${\displaystyle 2GM}$.

Когда какой-либо зонд (например, световой луч или наблюдатель) приближается к горизонту событий чёрной дыры, его временная координата Шварцшильда увеличивается до бесконечности. Уходящие на бесконечность нулевые геодехические в этой системе координат имеют бесконечное изменение t при выходе за горизонт. Черепашья координата бесконечно растёт с соответствующей скоростью и нивелирует сингулярное поведение в системах координат, построенных на её основе.

Увеличение временной координаты до бесконечности по мере приближения к горизонту событий является причиной того, почему информацию от любого зонда, отправленного через такой горизонт событий, нельзя получить обратно. И это несмотря на то, что сам зонд, тем не менее, может перемещаться за горизонт. Это также является причиной того, что пространственно-временная метрика чёрной дыры, выраженная в координатах Шварцшильда, становится сингулярной на горизонте — и, таким образом, не может использоваться для полного (во всей области пространства) изображения траектории падающего зонда.

Сжимающаяся система координат Эддингтона — Финкельштейна получаются заменой координаты t новой координатой ${\displaystyle v=t+r^{*}}$. В этих координатах метрику Шварцшильда можно записать как[5]

${\displaystyle ds^{2}=-\left(1-{\frac {2GM}{r}}\right)dv^{2}+2\,dv\,dr+r^{2}d\Omega ^{2}\,,}$

где принимается, что

${\displaystyle d\Omega ^{2}=d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}}$

стандартная риманова метрика на двумерной сфере единичного радиуса.

Аналогично, расширяющаяся система координат Эддингтона — Финкельштейна получаются заменой t на новую координату ${\displaystyle u=t-r^{*}}$. Тогда метрика даётся выражением[6]

${\displaystyle ds^{2}=-\left(1-{\frac {2GM}{r}}\right)du^{2}-2\,du\,dr+r^{2}d\Omega ^{2}\,.}$

В обеих этих системах координат метрика явно не имеет особенности на радиусе Шварцшильда (даже если одна компонента обращается в нуль на этом радиусе, определитель метрики по-прежнему не обращается в нуль, и обратная метрика также не имеет расходящихся членов в этой точке). Расширяющаяся система координат описывает выброс частиц из центра за пределы гравитационного радиуса, но при попытки использовать её для падающих частиц внутри гравитационного радиуса возникает сингулярность аналогичная шварцшильдовской. Для сжимающейся системы координат падающие частицы внутри гравитационного радиуса не имеют особенности, но сингулярность возникает при попытке описать выходящие частицы за пределом гравитационного радиуса. Сжимающаяся система коорлинат используется для описания гравитационного коллапса[7].

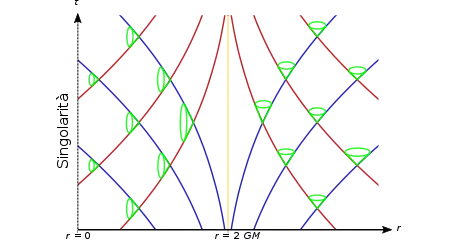
Для нулевых поверхностей v=const или ${\displaystyle v-2r^{*}}$=const или эквивалентно ${\displaystyle u+2r^{*}}$=const или u=const, полуается, что dv/dr и du/dr приближаются к 0 и ± 2 при больших r, а не к ± 1, как можно было бы ожидать, если считать u или v «временем». При построении диаграмм Эддингтона — Финкельштейна поверхности с постоянными u или v обычно рисуются в виде конусов, а постоянные линии u или v рисуются как наклонные под углом 45 градусов, а не как плоскости[8]. Некоторые источники вместо этого используют замену ${\displaystyle t'=t\pm (r^{*}-r)\,}$, что соответствует плоскостям на таких диаграммах. В этих координатах (для ${\displaystyle t'}$) метрика становится

${\displaystyle ds^{2}=-\left(1-{\frac {2GM}{r}}\right)dt'^{2}\pm {\frac {4GM}{r}}\,dt'\,dr+\left(1+{\frac {2GM}{r}}\right)\,dr^{2}+r^{2}d\Omega ^{2}=(-dt'^{2}+dr^{2}+r^{2}d\Omega ^{2})+{\frac {2GM}{r}}(dt'\pm dr)^{2}}$

что становится минковской при больших r. Эти временные координаты и метрики представили Эддингтон и Финкельштейн в своих статьях.

Это график световых конусов в координатах v-r, где ось v является прямой линией, наклонённой вверх влево. Синяя линия - пример одной из постоянных линий v=const. На графике показаны световые конусы при различных значениях r. Зелёные линии представляют собой различные постоянные линии u=const. Они приближаются к r = 2GM асимптотически. В этих координатах горизонт — это горизонт чёрной дыры (ничто не может его покинуть). Диаграмма для координат u-r — это та же но перевёрнутая диаграмма, с заменой местами u и v. В этом случае горизонт представляется белой дырой, то есть горизонт, из которого могут исходить материя и свет, но ничто не может войти внутрь.

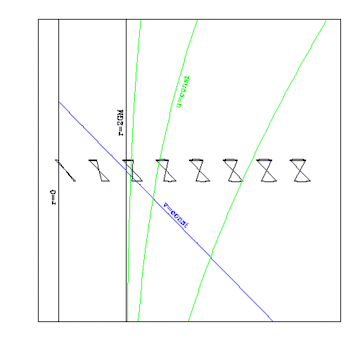
Координаты Эддингтона — Финкельштейна всё ещё неполны и могут быть расширены. Например, движущиеся на бесконечность времениподобная геодезические, определяемые (с собственным временем ${\displaystyle \tau }$)

${\displaystyle r(\tau )={\sqrt {2GM\tau }}}$

${\displaystyle {\begin{aligned}v(\tau )&=\int {\frac {r(\tau )}{r(\tau )-2GM}}\,d\tau \\&=C+\tau +2{\sqrt {2GM\tau }}+4GM\ln \left({\sqrt {\frac {\tau }{2GM}}}-1\right)\end{aligned}}}$

имеют v(τ) → −∞ по мере того, как τ → 2GM. То есть, эта времениподобная геодезическая имеет конечную собственную длину в прошлое, где она выходит из горизонта (r = 2GM), когда v стремится к ${\displaystyle -\infty }$. Области для конечных v и r < 2GM отличаются от конечных u и r < 2GM. Горизонт r = 2GM и конечный v (горизонт чёрной дыры) отличаются от горизонта с r = 2GM и конечным u (горизонт белой дыры).

Метрика в координатах Крускала — Секереша охватывает всё расширенное пространство-время Шварцшильда в единой системе координат. Его главный недостаток состоит в том, что в этих координатах метрика зависит как от временных, так и от пространственных координат. В системе координат Эддингтона — Финкельштейна, как и в координатах Шварцшильда, метрика не зависит от «времени» (либо t в Шварцшильде, либо u или v в различных системах координат Эддингтона — Финкельштейна), но ни одна из них не покрывает всё пространство-время[7].

Координаты Эддингтона — Финкельштейна имеют некоторое сходство с координатами Гуллстранда–Пенлеве в том, что обе они не зависят от времени и проникают (регулярны) либо в будущие (чёрная дыра), либо в прошлые (белая дыра) горизонты. Обе метрики не диагональны (гиперповерхности постоянного «времени» не ортогональны гиперповерхностям постоянного r). Последние имеют плоскую пространственную метрику, в то время как пространственные (постоянная «времени») гиперповерхности первых равны нулю и имеют ту же метрику, что и у светового конуса в пространстве Минковского (${\displaystyle t=\pm r}$ в плоском пространстве-времени).

• Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 3. — 510 с.