Класс PSPACE

Если для данной машины Тьюринга верно, что существует полином p(n), такой что на любом входе размера n она посетит не более p(n) клеток, то такая машина называется машиной Тьюринга с полиномиальным ограничением пространства.

Можно показать, что:

1. Если машина Тьюринга с пространством, полиномиально ограниченным p(n), то существует константа c, при которой эта машина допускает свой вход длины n не более, чем за ${\displaystyle c^{1+p(n)}}$ шагов.

Отсюда следует, что все языки машин Тьюринга с полиномиальным ограничением пространства — рекурсивные.

Класс языков PSPACE — множество языков, допустимых детерминированной машиной Тьюринга с полиномиальным ограничением пространства.

Класс языков NPSPACE — множество языков, допустимых недетерминированной машиной Тьюринга с полиномиальным ограничением пространства.

Для классов языков PSPACE и NPSPACE верны следующие утверждения:

1. PSPACE = NPSPACE (этот факт доказывается теоремой Сэвича)

2. Контекстно-зависимые языки являются подмножеством PSPACE

3. ${\displaystyle {\mbox{NL}}\subseteq {\mbox{P}}\subseteq {\mbox{NP}}\subseteq {\mbox{PSPACE}}\subseteq {\mbox{EXPTIME}}}$

4. ${\displaystyle {\mbox{NL}}\subsetneq {\mbox{PSPACE}}\subsetneq {\mbox{EXPSPACE}}}$

5. Если язык принадлежит PSPACE, то существует машина Тьюринга с полиномиальным ограничением пространства, такая что она остановится за ${\displaystyle c^{p(n)}}$ шагов для некоторого c и полинома p(n).

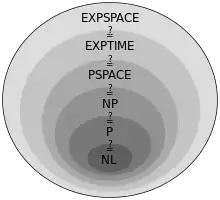
Известно, что хотя бы один из трёх символов включения ${\displaystyle \subseteq }$ в утверждении ${\displaystyle {\mbox{NL}}\subseteq {\mbox{P}}\subseteq {\mbox{NP}}\subseteq {\mbox{PSPACE}}}$ должен быть строгим ${\displaystyle (\subsetneq )}$ (то есть исключать равенство множеств, отношение между которыми он описывает), но неизвестно, который из них. Также хотя бы одно подмножество в утверждении ${\displaystyle {\mbox{P}}\subseteq {\mbox{NP}}\subseteq {\mbox{PSPACE}}\subseteq {\mbox{EXPTIME}}}$ должно быть собственным (то есть хотя бы один символ включения должен быть строгим). Есть предположение, что все эти включения строгие ${\displaystyle (\subsetneq )}$.

PSPACE-полная задача — это такая задача ${\displaystyle {\mbox{L}}\in {\mbox{PSPACE}},}$ к которой могут быть сведены по Карпу все проблемы класса PSPACE за полиномиальное время.

Про PSPACE-полную задачу известны следующие факты:

Если ${\displaystyle {\mbox{L}}}$ является PSPACE-полной задачей, то

1.${\displaystyle {\mbox{L}}\in {\mbox{P}}\Rightarrow {\mbox{P}}={\mbox{PSPACE}};}$

2.${\displaystyle {\mbox{L}}\in {\mbox{NP}}\Rightarrow {\mbox{NP}}={\mbox{PSPACE}}.}$

Пример PSPACE-полной задачи: нахождение истинных булевых формул с кванторами.

• Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман. Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: «Вильямс», 2002. — 528 с. — ISBN 0-201-44124-1.

• Hopcroft, Motwani, Ullman: «Introduction to Automata Theory, Languages, and Computation»