Классификации кубик Ньютона

Ньютон сделал по крайней мере три попытки исследовать кубики и получил две классификации кубик. Первая попытка была сделана в самом конце 1667 либо в начале 1668 года. Она завершилась написанием работы[1].

Первая классификация кубик была опубликована Ньютоном в 1704 году в работе[2]. Он описал 72 кубики. Позже Дж. Стирлинг[3] добавил 4 кубики, затем Ф. Николь[4] добавил ещё 2 кубики. Рисунки добавленных кубик можно найти в статье[5]. Эта классификация Ньютона получила широкую известность[6]. Подробное обсуждение классификации можно найти в обзорной статье[7].

В работе[2] Ньютон указал, что для любой кубики можно так подобрать систему координат, что она будет иметь одно из следующих четырёх уравнений:

• ${\displaystyle xy^{2}+ey=ax^{3}+bx^{2}+cx+d;}$
• ${\displaystyle xy=ax^{3}+bx^{2}+cx+d;}$
• ${\displaystyle y^{2}=ax^{3}+bx^{2}+cx+d;}$
• ${\displaystyle y=ax^{3}+bx^{2}+cx+d.}$

Ньютон исследовал эти уравнения, изучая условия, накладываемые на их коэффициенты. В результате кубики были подразделены на 14 родов и на 78 типов. Он различал кубики с разным расположением компонент кривой относительно её асимптот (если кривая их имеет). Ньютон не определил классы эквивалентности кубик, и в этом смысле его классификация не является строгой. Если продолжить идею Ньютона и классифицировать кубики вместе с её асимптотами, определив класс эквивалентности по правилу: две кубики эквивалентны, если их объединения с их асимптотами изотопны, и при изотопии сохраняется расположение точек перегиба кубики, то получится полная классификация, содержащая 99 типов (недостающие 21 типов описаны в приложении обзорной статьи[5]).

Вторая классификация была получена Ньютоном в его неопубликованной рукописи[8]. Эта классификация является классификацией сечений кубических конусов. Она содержит 59 сечений.

Рис. A: Взаимное расположение стандартных кубик с горизонталями

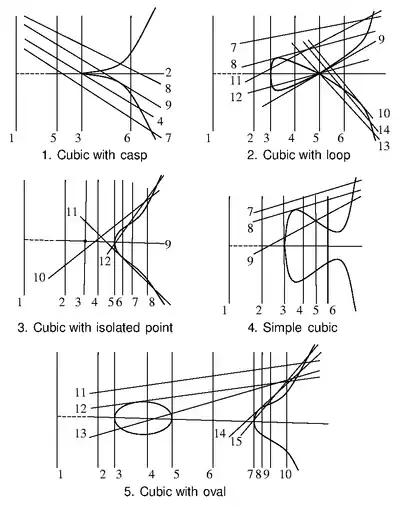
Ньютон начинает с пяти стандартных кубик:

1. кубика с точкой возврата — ${\displaystyle y^{2}=x^{3}}$;
2. кубика с петлёй — ${\displaystyle y^{2}=x^{2}(x+1)}$;
3. кубика с изолированной точкой — ${\displaystyle y^{2}=x^{2}(x-1)}$;
4. простая кубика — ${\displaystyle y^{2}=x[(x-1)^{2}+1]}$;
5. кубика с овалом — ${\displaystyle y^{2}=x(x+1)(x+2)}$.

Для каждой из этих пяти кубик он описывает её взаимные расположения с прямыми линиями, которые он называет горизонталями, см. рис. A.

Рис. B: Пять стандартных конусов третьей степени

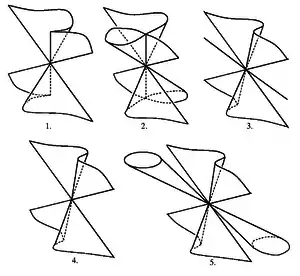
Затем Ньютон рассматривает пять кубических конусов, направляющими которых являются эти стандартные кубики, см. рис. B.

Далее для каждой выбранной горизонтали он рассматривает вспомогательную плоскость, проходящую через эту горизонталь и вершину конуса. Наконец, он проводит произвольную плоскость, параллельную вспомогательной плоскости, которая пересекает конус вдоль искомого сечения. При проектировании этого сечения из вершины конуса горизонталь отображается на бесконечно удалённую прямую плоскости сечения. Это означает, что выбор горизонтали эквивалентен выбору бесконечно удалённой прямой. На рис. A сохранена ньютонова нумерация горизонталей. Заметим, что, во-первых, на всех рисунках A.1 — A.5 горизонталь с номером 1 является бесконечно удалённой прямой для нарисованной аффинной плоскости, во-вторых, на рис. A.3, A.4 и A.5 горизонтали с номерами соответственно 7, 5 и 9 пересекают кубику в трёх точках перегиба (одна из них — бесконечно удалённая).

В результате этих построений Ньютон получает:

9 сечений из кубики с точкой возврата;

14 сечений из кубики с петлёй,

12 сечений из кубики с изолированной точкой,

9 сечений из простой кубики,

15 сечений из кубики с овалом.

Всего 59 сечений.

• 
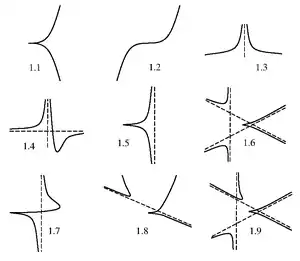  Рис. 1: Ньютоновы сечения, полученные из кубики с точкой возврата
• 
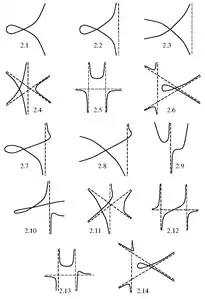  Рис. 2: Ньютоновы сечения, полученные из кубики с петлёй
• 
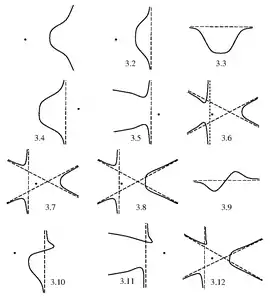  Рис. 3: Ньютоновы сечения, полученные из кубики с изолированной точкой
• 
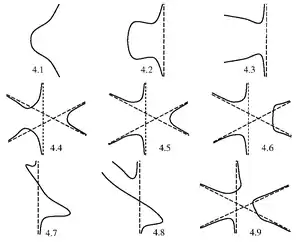  Рис. 4: Ньютоновы сечения, полученные из простой кубики
• 
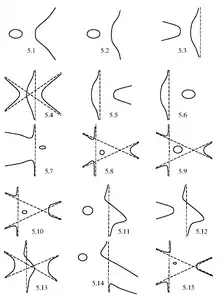  Рис. 5: Ньютоновы сечения, полученные из кубики с овалом

Из текста рукописи Ньютона следует, что описанные им классы эквивалентности подчиняются следующему современному определению.

Пусть ${\displaystyle \mathbb {R} ^{2}=\mathbb {R} P^{2}\setminus L}$ — аффинная карта проективной плоскости, для которой прямая ${\displaystyle L}$ выбрана в качестве бесконечно удалённой прямой, пусть ${\displaystyle C_{0},C_{1}\subset \mathbb {R} ^{2}}$ — аффинные кубики. Говорят, что кубики ${\displaystyle C_{0},C_{1}}$ реализуют одно и тот же кубическое сечение, если существует изотопия троек ${\displaystyle F_{t}:(\mathbb {R} P^{2},C_{0}\cup L,L)\to (\mathbb {R} P^{2},C_{1}\cup L,L)}$, такая что

1. для любого ${\displaystyle t\in [0,1]}$ образ сокращения ${\displaystyle F_{t}{\big |}_{C_{0}\cup L}}$ является объединением нераспадающейся кубики и прямой;
2. если ${\displaystyle x\in C_{0}}$ является либо регулярной точкой кубики ${\displaystyle C_{0}}$, либо её точкой перегиба, либо её особой точкой, то каждая точка пути ${\displaystyle F_{t}{\big |}_{x}}$ является соответственно такой же точкой кубики ${\displaystyle C_{t}}$.

В рукописи[8] Ньютон описал эти классы словесно. Рисунки кубических сечений были, по-видимому, впервые опубликованы в обзорной статье[5]. Они приведены здесь в новой редакции.

Используя ньютонову классификацию кубических сечений, А. Б. Корчагин[9] получил аффинную классификацию кубик.