Аффинная классификация кубик

Исаак Ньютон получил две классификации кубик[1] [2]. Основываясь на второй классификации[2] была получена аффинная классификация кубик[3]. Эта классификация описана в следующей теореме.

Теорема. Существуют 59 семейств аффинных классов эквивалентности неприводимых кубик: 15 классов модальности 0;  23 семейства (классов) модальности 1;  16 семейств модальности 2;  5 семейств модальности 3;  эти семейства представлены в следующем списке канонических уравнений.

Порядок перечисления семейств аффинных классов принадлежит Ньютону, для удобства он сохранён в этом списке. В каждом пункте списка указана размерность множества кубик, принадлежащих этому семейству аффинных классов. Например, каждая кубика аффинного класса с номером 1.1 аффинно эквивалентна кубике   ${\displaystyle y^{2}=x^{3}}$,   множество кубик этого класса в пространстве   ${\displaystyle \mathbb {R} P^{9}}$   всех кубик имеет размерность   ${\displaystyle \dim =5}$,   а каждая кубика семейства аффинных классов с номером 1.7 аффинно эквивалентна одной из кубик однопараметрического семейства   ${\displaystyle (x-1)y^{2}-ax^{2}y+x^{3}=0}$, где   ${\displaystyle 0<a<2}$,   множество кубик этого семейства в пространстве   ${\displaystyle \mathbb {R} P^{9}}$   всех кубик имеет размерность   ${\displaystyle \dim =7}$.

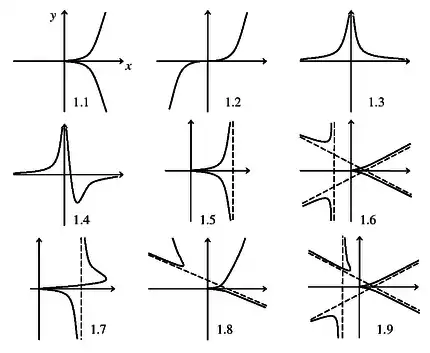
Классы, полученные из кубики с точкой возврата, см. рис. 1.

1.1.   ${\displaystyle y^{2}=x^{3}}$;  ${\displaystyle \dim =5}$.

1.2.   ${\displaystyle y=x^{3}}$;  ${\displaystyle \dim =5}$.

1.3.   ${\displaystyle x^{2}y=1}$;  ${\displaystyle \dim =6}$.

1.4.   ${\displaystyle x^{2}y=1-x}$;  ${\displaystyle \dim =6}$.

1.5.   ${\displaystyle (x-1)y^{2}+x^{3}=0}$;  ${\displaystyle \dim =6}$.

1.6.   ${\displaystyle (x+1)y^{2}=x^{3}}$;  ${\displaystyle \dim =6}$.

1.7.   ${\displaystyle (x-1)y^{2}-ax^{2}y+x^{3}=0}$,   где ${\displaystyle 0<a<2}$;  ${\displaystyle \dim =7}$.

1.8.   ${\displaystyle y^{2}-x^{2}y-x^{3}=0}$;  ${\displaystyle \dim =6}$.

1.9.   ${\displaystyle (x+1)y^{2}-ax^{2}y+x^{3}=0}$,   где ${\displaystyle a>0}$;  ${\displaystyle \dim =7}$.

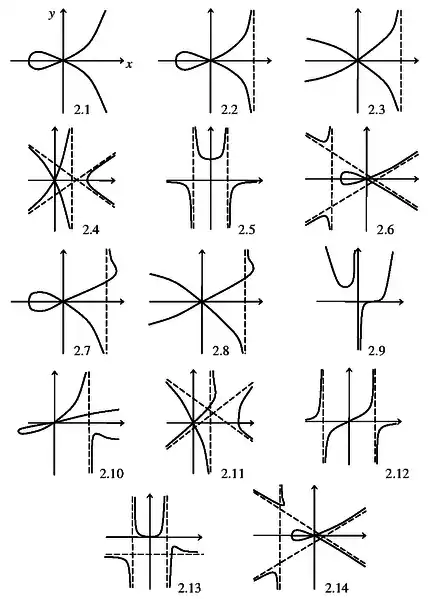
Классы, полученные из кубики с петлёй, см. рис. 2.

2.1.   ${\displaystyle y^{2}=x^{2}(x+1)}$;   ${\displaystyle \dim =6}$.

2.2.   ${\displaystyle \left(1-{\frac {x}{a}}\right)y^{2}=x^{2}\left(x+1\right)}$,  где ${\displaystyle a>0}$;  ${\displaystyle \dim =7}$.

2.3.   ${\displaystyle \left(1-x\right)y^{2}=x^{2}}$;  ${\displaystyle \dim =6}$.

2.4.   ${\displaystyle \left(1-{\frac {x}{a}}\right)y^{2}=x^{2}\left(1-x\right)}$,  где ${\displaystyle 0<a<1}$;  ${\displaystyle \dim =6}$.

2.5.   ${\displaystyle (x+1)(x-1)y+1=0}$;  ${\displaystyle \dim =6}$.

2.6.   ${\displaystyle \left({\frac {x}{a}}+1\right)y^{2}=x^{2}\left(x+1\right)}$,  где ${\displaystyle a>1}$;  ${\displaystyle \dim =7}$.

2.7.   ${\displaystyle \left(x-1\right)y^{2}=bx(x+a)(y-x)}$,  где ${\displaystyle a>0}$  и  ${\displaystyle 0\leq b<4}$;  ${\displaystyle \dim =8}$.

2.8.   ${\displaystyle (x-1)y^{2}=ax(y-x)}$,  где ${\displaystyle a>0}$;  ${\displaystyle \dim =7}$.

2.9.   ${\displaystyle xy=(x-1)^{3}}$;  ${\displaystyle \dim =6}$.

2.10.   ${\displaystyle (x-1)y^{2}=ax(y-x)}$,  где ${\displaystyle a<-4}$;  ${\displaystyle \dim =7}$.

2.11.   ${\displaystyle \left(1-x\right)y^{2}=bx\left(x-a\right)\left(y-x\right)}$,  где ${\displaystyle a>1}$  и  ${\displaystyle b>0}$;  ${\displaystyle \dim =8}$.

2.12.   ${\displaystyle (x+1)(x-a)y+x=0}$,  где ${\displaystyle a>0}$;  ${\displaystyle \dim =7}$.

2.13.   ${\displaystyle (x+1)(x-a)y+x^{2}=0}$,  где ${\displaystyle a>0}$  и  ${\displaystyle a\neq 1}$;  ${\displaystyle \dim =7}$.

2.14.   ${\displaystyle \left({\frac {x}{a}}+1\right)y^{2}-bx^{2}y=x^{2}\left(x+1\right)}$,  где ${\displaystyle a>0}$  и  ${\displaystyle b>0}$;  ${\displaystyle \dim =8}$.

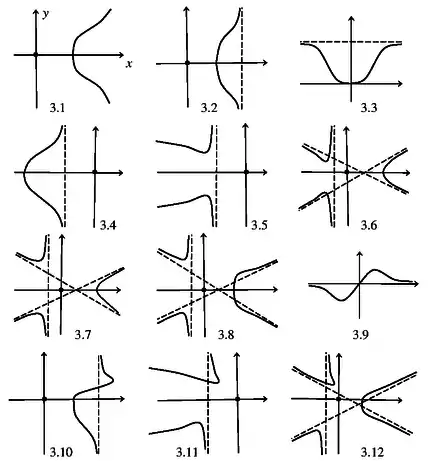
Классы, полученные из кубики с изолированной точкой, см. рис. 3, где кубики семейств с номерами 3.1, 3.2, 3.4 - 3.8, 3.10 - 3.12 имеют изолированную точку в начале координат ${\displaystyle O=(0,0)}$, а кубики семейств с номерами 3.3 и 3.9 имеют изолированную тоску в точке пересечения прямой ${\displaystyle x=0}$ и бесконечно удалённой прямой ${\displaystyle z=0}$, т.е. в точке с проективными координатами ${\displaystyle (0:1:0)}$.

3.1.   ${\displaystyle y^{2}=x^{2}(x-1)}$;  ${\displaystyle \dim =6}$.

3.2.   ${\displaystyle \left(1-{\frac {x}{a}}\right)y^{2}=x^{2}\left(x-1\right)}$,  где ${\displaystyle a>1}$;  ${\displaystyle \dim =7}$.

3.3.   ${\displaystyle (x^{2}+1)y=x^{2}}$;  ${\displaystyle \dim =6}$.

3.4.   ${\displaystyle \left({\frac {x}{a}}+1\right)y^{2}=-x^{2}\left(x+1\right)}$,  где ${\displaystyle 0<a<1}$;  ${\displaystyle \dim =7}$.

3.5.   ${\displaystyle \left(x+1\right)y^{2}=-x^{2}}$;  ${\displaystyle \dim =6}$.

3.6.   ${\displaystyle \left({\frac {x}{a}}+1\right)y^{2}=x^{2}\left(x-1\right)}$,  где ${\displaystyle 0<a<{\frac {1}{3}}}$;  ${\displaystyle \dim =7}$.

3.7.   ${\displaystyle \left(3x+1\right)y^{2}=x^{2}\left(x-1\right)}$;  ${\displaystyle \dim =6}$.

3.8.   ${\displaystyle \left({\frac {x}{a}}+1\right)y^{2}=x^{2}\left(x-1\right)}$,  где ${\displaystyle a>{\frac {1}{3}}}$;  ${\displaystyle \dim =7}$.

3.9.   ${\displaystyle y(x^{2}+ax+1)=x}$,  где ${\displaystyle 0\leq a<2}$;  ${\displaystyle \dim =7}$.

3.10.     ${\displaystyle (1-x)y^{2}+bx(x-a)(y-x)=0}$,  где ${\displaystyle 0<a<1}$  и   ${\displaystyle 0<b<4}$;  ${\displaystyle \dim =8}$.

3.11.   ${\displaystyle (x+1)y^{2}+ax(y+x)=0}$,  где ${\displaystyle 0<a<4}$;  ${\displaystyle \dim =7}$.

3.12.   ${\displaystyle \left(x+1\right)y^{2}-bx(x-a)(y+x)=0}$,  где ${\displaystyle a>0}$,  ${\displaystyle b>0}$  и  ${\displaystyle a<{\frac {(a+1)(b+2-{\sqrt {b^{2}+4b}})}{2(b+4)-(a+1)\left(b+2+{\sqrt {b^{2}+4b}}\right)}}}$;  ${\displaystyle \dim =8}$.

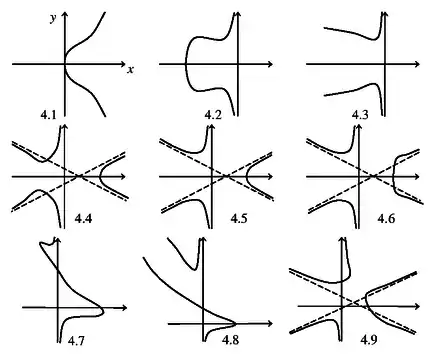
Классы, полученные из простой кубики, см. рис. 4.

4.1.   ${\displaystyle y^{2}=x\left[\left(x-a\right)^{2}+1\right]}$,  где ${\displaystyle a\in \mathbb {R} }$;  ${\displaystyle \dim =7}$.

4.2.   ${\displaystyle xy^{2}=-(x+a)\left[\left(x-b\right)^{2}+1\right]}$,  где ${\displaystyle a>0}$  и  ${\displaystyle b\in \mathbb {R} }$;  ${\displaystyle \dim =8}$.

4.3.   ${\displaystyle xy^{2}=-\left[\left(x-a\right)^{2}+1\right]}$, где ${\displaystyle a\in \mathbb {R} }$;  ${\displaystyle \dim =7}$.

4.4.   ${\displaystyle xy^{2}=-(x-a)\left[\left(x-b\right)^{2}+1\right]}$, где ${\displaystyle a>0}$ и ${\displaystyle b<{\frac {a^{2}-4}{4a}}}$;  ${\displaystyle \dim =8}$.

4.5.   ${\displaystyle xy^{2}=-(x-a)\left[\left(x-{\frac {a^{2}-4}{4a}}\right)^{2}+1\right]}$,  где ${\displaystyle a>0}$;  ${\displaystyle \dim =7}$.

4.6.   ${\displaystyle xy^{2}=-(x-a)\left[\left(x-b\right)^{2}+1\right]}$, где ${\displaystyle a>0}$ и ${\displaystyle b>{\frac {a^{2}-4}{4a}}}$;  ${\displaystyle \dim =8}$.

4.7.   ${\displaystyle xy^{2}=c[(x-a)^{2}+1](y+x-b)}$,  где ${\displaystyle a\in \mathbb {R} }$,  ${\displaystyle b\geq 0}$  и  ${\displaystyle -4<c<0}$;  ${\displaystyle \dim =9}$.

4.8.   ${\displaystyle xy^{2}=-4[(x-a)^{2}+1](y+x-b)}$,  где ${\displaystyle a\in \mathbb {R} }$,  ${\displaystyle b\geq 0}$  и  ${\displaystyle b\neq 2a}$;  ${\displaystyle \dim =8}$.

4.9.   ${\displaystyle xy^{2}=c[(x-a)^{2}+1](y+x-b)}$,  где ${\displaystyle a\in \mathbb {R} }$,  ${\displaystyle b\geq 0}$,  ${\displaystyle {\sqrt {c(c+4)(a^{2}+1)}}<ac-2b}$,  ${\displaystyle 0<c<2\left[a^{2}-ab+1+{\sqrt {(a^{2}-ab+1)^{2}+b^{2}}}\right]}$,  ${\displaystyle {\frac {ac+2b+{\sqrt {(ac+2b)^{2}-c(c+4)(a^{2}+1)}}}{c+4}}<{\frac {(c+4)(a^{2}+1)(\beta -b)}{(2a-b)^{2}-(c+4)(a^{2}+1)(\alpha +1)}}}$,  ${\displaystyle {\sqrt {c(c+4)(a^{2}+1)}}<ac+2b}$,  ${\displaystyle \alpha ={\frac {c-{\sqrt {c^{2}+4c}}}{2}}}$  и   ${\displaystyle \beta =-c\left[a-{\frac {a(c+2)+b}{\sqrt {c^{2}+4c}}}\right]}$;  ${\displaystyle \dim =9}$.

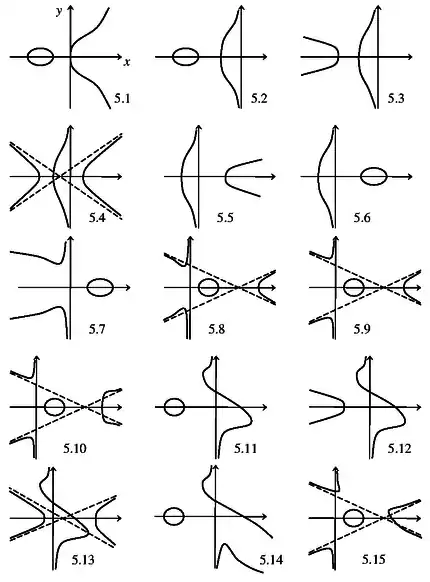
Классы, полученные из кубики с овалом, см. рис. 5.

5.1.   ${\displaystyle y^{2}=x(x+1)(x+a)}$,  где ${\displaystyle a>1}$;  ${\displaystyle \dim =7}$.

5.2.   ${\displaystyle xy^{2}=-(x+1)(x+a)(x+b)}$,  где ${\displaystyle 1<a<b}$;  ${\displaystyle \dim =8}$.

5.3.   ${\displaystyle xy^{2}=-(x+1)(x+a)}$,  где ${\displaystyle a>1}$;  ${\displaystyle \dim =7}$.

5.4.   ${\displaystyle xy^{2}=-(x+a)(x+1)(x-b)}$,  где ${\displaystyle a>1}$  и  ${\displaystyle b>0}$;  ${\displaystyle \dim =8}$.

5.5.   ${\displaystyle xy^{2}=(x+1)(x-a)}$,  где ${\displaystyle a>0}$;  ${\displaystyle \dim =7}$.

5.6.   ${\displaystyle xy^{2}=-(x+1)(x-a)(x-b)}$, где ${\displaystyle 0<a<b}$; ${\displaystyle \dim =8}$.

5.7.   ${\displaystyle xy^{2}=-(x-1)(x-a)}$,  где ${\displaystyle a>1}$;   ${\displaystyle \dim =7}$.

5.8.   ${\displaystyle xy^{2}=(x-a)(x-1)(x-b)}$,  где ${\displaystyle 0<a<1<b}$ и ${\displaystyle b>({\sqrt {a}}+1)^{2}}$;  ${\displaystyle \dim =8}$.

5.9.   ${\displaystyle xy^{2}=(x-a)(x-1)[x-({\sqrt {a}}+1)^{2}]}$,  где ${\displaystyle 0<a<1}$;  ${\displaystyle \dim =7}$.

5.10.   ${\displaystyle xy^{2}=(x-a)(x-1)(x-b)}$,  где ${\displaystyle 0<a<1<b}$  и  ${\displaystyle b<({\sqrt {a}}+1)^{2}}$;  ${\displaystyle \dim =8}$.

5.11.   ${\displaystyle xy^{2}=c(x+1)(x+a)(x+y-b)}$,  где ${\displaystyle a>1}$,  ${\displaystyle b>-1}$  и  ${\displaystyle -4<c<0}$;  ${\displaystyle \dim =9}$.

5.12.   ${\displaystyle xy^{2}=b(x+1)(x+y-a)}$,  где ${\displaystyle a>-1}$  и  ${\displaystyle b\in \mathbb {R} }$;  ${\displaystyle \dim =8}$.

5.13.   ${\displaystyle xy^{2}=c(x+1)(x-a)(x+y-b)}$,  где ${\displaystyle a>0}$,  ${\displaystyle -1<b<a}$  и  ${\displaystyle c>0}$;  ${\displaystyle \dim =9}$.

5.14.   ${\displaystyle xy^{2}=-4(x+1)(x+a)(x+y-b)}$,  где ${\displaystyle a>1}$  и  ${\displaystyle b>-1}$;  ${\displaystyle \dim =8}$.

5.15.   ${\displaystyle xy^{2}=c(x-a)(x-1)(x+y-b)}$,   где ${\displaystyle 0<a<1<b}$,  ${\displaystyle c>0}$,  ${\displaystyle {\frac {ac\left(\beta -b\right)}{\beta ^{2}-c\left[a\left(\alpha +1\right)-(a+1)\left(\beta -b\right)\right]}}>{\frac {c(a+1)+4b+{\sqrt {\mathcal {D}}}}{2(c+4)}}}$,  ${\displaystyle {\mathcal {D}}=[c(a-1)+4b]^{2}+16c(b-a)}$,   ${\displaystyle \alpha ={\frac {c-{\sqrt {c^{2}+4c}}}{2}}}$,  ${\displaystyle \beta ={\frac {c\left[b+(a+1)\left(\alpha +1\right)\right]}{c-2\alpha }}}$;  ${\displaystyle \dim =9}$.