Категория запятой

В теории категорий, категория запятой — специальная конструкция, предоставляющая способ изучения морфизмов не как соотнесений объектов категории друг с другом, а как самостоятельных объектов. Название «категория запятой» появилось из-за первоначального (придуманного Ловером) обозначения, которое включало в себя знак запятой. Впоследствии стандартное обозначение изменилось из соображений удобства.

Определение

Общий случай

Пусть ${\mathcal {A}},{\mathcal {B}}$ и ${\mathcal {C}}$ — категории, а $S$ и $T$ — функторы

{\mathcal {A}}{\xrightarrow {\;\;S\;\;}}{\mathcal {C}}{\xleftarrow {\;\;T\;\;}}{\mathcal {B}}

Категорию запятой $(S\downarrow T)$ можно построить следующим образом:

Объекты — все тройки вида $(\alpha ,\beta ,f)$ , где $\alpha$ — объект ${\mathcal {A}}$ , $\beta$ — объект ${\mathcal {B}}$ , и $f:S(\alpha )\rightarrow T(\beta )$ — морфизм в ${\mathcal {C}}$ .
Морфизмы из $(\alpha ,\beta ,f)$ в $(\alpha ',\beta ',f')$ — все пары $(g,h)$ , где $g:\alpha \rightarrow \alpha '$ , $h:\beta \rightarrow \beta '$ — морфизмы в ${\mathcal {A}}$ и ${\mathcal {B}}$ соответственно, такие что следующая диаграмма коммутирует:

${\begin{matrix}S(\alpha )&{\xrightarrow {S(g)}}&S(\alpha ')\\f{\Bigg \downarrow }&&{\Bigg \downarrow }f'\\T(\beta )&{\xrightarrow[{T(h)}]{}}&T(\beta ')\end{matrix}}$

Композиция морфизмов $(g,h)\circ (g',h')$ берется как $(g\circ g',h\circ h')$ , если последнее выражение определено. Тождественный морфизм объекта $(\alpha ,\beta ,f)$ — это $(\mathrm {id} _{\alpha },\mathrm {id} _{\beta })$ .

Два частных случая

Рассмотрим два частных случая, которые более просты и встречаются очень часто.

Первый случай — категория объектов над $A$ . Пусть в предыдущем определении ${\mathcal {A}}={\mathcal {C}}$ , $S$ — тождественный функтор и ${\mathcal {B}}={\textbf {1}}$ (категория с одним объектом $*$ и одним морфизмом). Тогда $T(*)=A$ для некоторого объекта $A$ категории ${\mathcal {C}}$ . В этом случае используют обозначение $({\mathcal {C}}\downarrow A)$ . Объекты вида $(\alpha ,*,f)$ — это просто пары $(\alpha ,f)$ , где $f:\alpha \rightarrow A$ . Иногда в этой ситуации $f$ обозначают как $\pi _{\alpha }$ . Морфизм из $(B,\pi _{B})$ в $(B',\pi _{B'})$ — это морфизм $g:B\rightarrow B'$ , замыкающий следующую диаграмму до коммутативной:

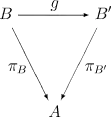
Двойственный случай — категория объектов под $A$ . Здесь $S$ — функтор из 1 и $T$ — тождественный функтор. В этом случае используют обозначение $(A\downarrow {\mathcal {C}})$ , где $A$ — объект ${\mathcal {C}}$ , в который отображает $S$ . Объекты — пары $(B,i_{B})$ , где $i_{B}:A\rightarrow B$ . Морфизм между $(B,i_{B})$ и $(B',i_{B'})$ — отображение $h:B\rightarrow B'$ , замыкающее следующую диаграмму до коммутативной:

Категория стрелок

Ещё один частный случай — когда $S$ и $T$ — тождественные функторы в ${\mathcal {C}}$ (так что ${\mathcal {A}}={\mathcal {B}}={\mathcal {C}}$ ). В этом случае категория запятой называется категорией стрелок ${\mathcal {C}}^{\rightarrow }$ . Её объекты — морфизмы ${\mathcal {C}}$ , а её морфизмы — коммутативные квадраты в ${\mathcal {C}}$ .[1]

Свойства

Для любой категории стрелок определены два забывающих функтора из неё:

Функтор прообраза $S\downarrow T\to {\mathcal {A}}$ $\text{[math]}$ , который отображает:
- объекты: $(\alpha ,\beta ,f)\mapsto \alpha$ ;
- морфизмы: $(g,h)\mapsto g$ ;
Функтор образа, $S\downarrow T\to {\mathcal {B}}$ $\text{[math]}$ , который отображает:
- объекты: $(\alpha ,\beta ,f)\mapsto \beta$ ;
- морфизмы: $(g,h)\mapsto h$ .

Примеры

Категория множеств с отмеченной точкой — это категория запятой $\scriptstyle {(\bullet \downarrow \mathbf {Set} )}$ , где $\scriptstyle {\bullet }$ — функтор, выбирающий некоторый синглетон и $\scriptstyle {\mathbf {Set} }$ — тождественный функтор в категории множеств. Сходным образом можно образовать категорию топологических пространств с отмеченной точкой $\scriptstyle {(\bullet \downarrow \mathbf {Top} )}$ .
Категория графов — это категория запятой $\scriptstyle {(\mathbf {Set} \downarrow D)}$ , где $\scriptstyle {D:\mathbf {Set} \rightarrow \mathbf {Set} }$ — функтор, отправляющий $s$ в $s\times s$ . Объекты вида $(a,b,f)$ состоят из двух множеств и функции; $a$ — индексирующее множество для ребер, $b$ — множество вершин, тогда $f:a\rightarrow (b\times b)$ выбирает пару элементов $b$ для каждого $a$ , то есть $f$ выбирает определенное ребро из множества возможных ребер $b\times b$ . Морфизмы в этой категории — функции на индексирующем множестве и множестве вершин, такие что образы вершин, соответствовавших данному ребру, будут соответствовать его образу.

Сопряжения

Функторы $F:{\mathcal {C}}\rightarrow {\mathcal {D}}$ и $G:{\mathcal {D}}\rightarrow {\mathcal {C}}$ сопряжены тогда и только тогда, когда категории запятой $(F\downarrow id_{\mathcal {D}})$ и $(id_{\mathcal {C}}\downarrow G)$ изоморфны, причем эквивалентные элементы проектируются на один и тот же элемент ${\mathcal {C}}\times {\mathcal {D}}$ . Это позволяет описать сопряженные функторы, не используя множества, и это было главной причиной появления конструкции категорий запятой.

Естественные преобразования

Если образы $S,T$ совпадают, то диаграмма, определяющая морфизм в $S\downarrow T$ с $\alpha =\beta ,\alpha '=\beta ',g=h$ совпадает с диаграммой, определяющей естественное преобразование $S\to T$ . Различие между двумя определениями состоит в том, что естественное преобразование — это определенный класс морфизмов вида $S(\alpha )\to T(\alpha )$ , тогда как объекты категории запятой — это все морфизмы такого вида. Функтор в категорию запятой может выбрать конкретное семейство морфизмов. И действительно, естественному преобразованию $\eta :S\to T$ , где $S,T:{\mathcal {A}}\to {\mathcal {C}}$ соответствует функтор ${\mathcal {A}}\to (S\downarrow T)$ который отображает объект $\alpha$ в $(\alpha ,\alpha ,\eta _{\alpha })$ и морфизмы $g$ в $(g,g)$ . Это задает биекцию между естественными преобразованиями $S\to T$ и функторами ${\mathcal {A}}\to (S\downarrow T)$ , которые являются левыми обратными обоих забывающих функторов из $S\downarrow T$ .

Примечания

Adámek, Jiří; Horst Herrlich, and George E. Strecker. Abstract and Concrete Categories (неопр.). — John Wiley & Sons, 1990. — ISBN 0-471-60922-6.

Литература

С. Маклейн Категории для работающего математика, — М.: ФИЗМАТЛИТ, 2004. — 352 с. — ISBN 5-9221-0400-4.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[joy-1] Adámek, Jiří; Horst Herrlich, and George E. Strecker. Abstract and Concrete Categories (неопр.). — John Wiley & Sons, 1990. — ISBN 0-471-60922-6.