Дерево Калкина — Уилфа
Дерево Ка́лкина — Уи́лфа (англ. Calkin—Wilf tree) — ориентированное двоичное дерево, в вершинах которого расположены положительные рациональные дроби согласно следующему правилу:
- корень дерева — дробь ;
- вершина с дробью имеет двух потомков: (левый) и (правый).
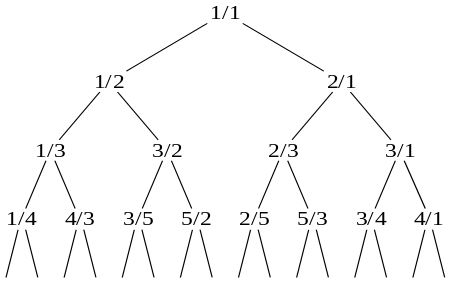
Дерево описано Нейлом Калкином и Гербертом С. Уилфом (2000[1]) в связи с задачей явного пересчёта[2] множества рациональных чисел.
Свойства дерева Калкина — Уилфа
Основные свойства
- Все дроби, расположенные в вершинах дерева, несократимы;
- Любая несократимая рациональная дробь встречается в дереве в точности один раз.
Последовательность Калкина — Уилфа
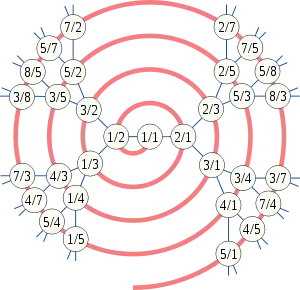
Из приведенных выше свойств следует, что последовательность положительных рациональных чисел, получаемая в результате обхода «в ширину»[3] (англ. breadth-first traversal) дерева Калкина — Уилфа (называемая также последовательностью Калкина — Уилфа; см. иллюстрацию),
определяет взаимно однозначное соответствие между множеством натуральных чисел и множеством положительных рациональных чисел.
Данная последовательность может быть задана рекуррентным соотношением[4]
где и обозначают соответственно целую и дробную части числа .
В последовательности Калкина — Уилфа знаменатель каждой дроби равен числителю следующей.
Функция fusc
В 1976 году Э. Дейкстра определил на множестве натуральных чисел целочисленную функцию fusc(n) следующими рекуррентными соотношениями[5]:
- ;
- ;
- .
Последовательность значений совпадает с последовательностью числителей дробей в последовательности Калкина — Уилфа, то есть последовательностью
- 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, …
Таким образом (поскольку знаменатель каждой дроби в последовательности Калкина — Уилфа равен числителю следующей), -й член последовательности Калкина — Уилфа равен , а соответствие
является взаимно однозначным соответствием между множеством натуральных чисел и множеством положительных рациональных чисел.
Функция может быть, помимо указанных выше рекуррентных соотношений, определена следующим образом.
- Значение равно количеству гипердвоичных (англ. hyperbinary) представлений числа , то есть представлений в виде суммы неотрицательных степеней двойки, где каждая степень встречается не более двух раз[6]. Например, число 6 представляется тремя такими способами:
- 6 = 4 + 2 = 4 + 1 + 1 = 2 + 2 + 1 + 1, поэтому .
- Значение равно числу всех нечётных биномиальных коэффициентов вида , где [7].
В оригинальной статье Калкина и Уилфа функция не упоминается, но рассматривается целочисленная функция , определённая для , равная количеству гипердвоичных представлений числа , и доказывается, что соответствие
является взаимно однозначным соответствием между множеством неотрицательных целых чисел и множеством рациональных чисел. Таким образом, для имеют место соотношения
См. также
Примечания
- См. статью Calkin, Wilf (2000) в списке литературы.
- То есть явного задания взаимно однозначного соответствия между множеством натуральных чисел и множества (положительных) рациональных чисел. Стандартные доказательства счётности множества рациональных чисел обычно не используют явное задание указанного соответствия.
- В данном случае обход «в ширину» соответствует последовательному обходу каждого уровня (начиная с верхнего) дерева Калкина — Уилфа слева направо (см. первую иллюстрацию).
- Найдено Моше Ньюменом (Moshe Newman); см. книгу Айгнера и Циглера в списке литературы, с. 108.
- Документ EWD 570: An exercise for Dr. R. M. Burstall; воспроизведен в книге Dijkstra (1982) (см. список литературы), pp. 215—216.
- При этом считается, что число 0 обладает единственным («пустым») гипердвоичным представлением 0 = 0, поэтому .
- См. Carlitz, L. A problem in partitions related to the Stirling numbers // Bulletin of the American Mathematical Society. — 1964. — Vol. 70, № 2. — P. 275—278. В этой статье определяется функция , которая оказывается связанной с функцией fusc соотношением .
Литература
- Calkin, N., Wilf H. S. Recounting the Rationals // The American Mathematical Monthly. — 2000. — Vol. 107, № 4. — P. 360—363. (JSTOR 2589182)
- Айгнер М., Циглер Г. Доказательства из Книги. Лучшие доказательства со времён Евклида до наших дней (пер. с англ.). — М.: Мир, 2006. — С. 105—109. — 256 с. — ISBN 5-03-003690-3. (NB: в данном переводе фамилия Wilf транскрибируется как «Вилф».)
- Dijkstra, E. W. Selected Writings on Computing: A Personal Perspective. — Springer-Verlag, 1982. — ISBN 0-387-90652-5. (См. документы EWD 570 и EWD 578, воспроизведенные в этой книге.)
- Stern M. Über eine zahlentheoretische Funktion // Journal für die reine und angewandte Mathematik. — 1858. — Т. 55. — С. 193—220.
- Щетников А. И. Алгоритм разворачивания всех числовых отношений из отношения равенства и идеальные числа Платона // ΣΧΟΛΗ. — 2008. — Т. 2. — С. 55—74. — ISSN 1995-4328.
