Двойной маятник
В физике и математике, в отрасли динамических систем, двойной маятник — это маятник с другим маятником, прикреплённым к его концу. Двойной маятник является простой физической системой, которая проявляет разнообразное динамическое поведение со значительной зависимостью от начальных условий[1]. Движение маятника руководствуется связанными обыкновенными дифференциальными уравнениями. Для некоторых энергий его движение является хаотическим.

Анализ
Можно рассматривать несколько вариантов двойных маятников: два звена могут быть одинаковыми или иметь разную длину и вес; они могут быть простыми маятниками или физическими маятниками; движение может происходить в трёх измерениях или быть ограничено вертикальной плоскостью. В следующем анализе звенья избраны как одинаковые физические маятники длины и массы , и их движение ограничено двумя измерениями.
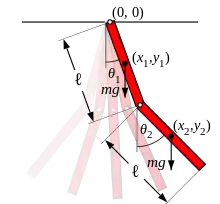
У физического маятника масса распределена вдоль всей его длины. Если масса распределена равномерно, тогда центр масс каждого звена совпадает с его геометрическим центром, и звено имеет такой момент инерции относительно этой точки.
Удобно использовать углы между каждым звеном и вертикалью как обобщённые координаты, определяя пространство конфигураций системы. Если положить начало координат декартовой системы координат в точке подвешивания первого маятника, тогда центр масс этого маятника находится в:
и центр масс другого в
Этой информации достаточно для того чтобы записать Лагранжиан.
Лагранжиан
Лагранжиан является разницей между кинетической энергией и потенциальной энергией:
Первое слагаемое это линейная кинетическая энергия центра масс тел, второе слагаемое это вращательная кинетическая энергия центров масс каждого из стержней. Последнее слагаемое это потенциальная энергия тел в однородном гравитационном поле.
Подставив координаты и перегруппируя уравнения имеем



Обобщенные импульсы можно записать как
Эти выражения можно преобразовать, чтобы получить
Уравнения движения, получаемые из уравнений Эйлера — Лагранжа, можно записать как
Последние четыре уравнения являются явными формулами для временной эволюций системы с заданным текущим состоянием. Невозможно продвинуться дальше и интегрировать эти уравнения аналитически, чтобы получить формулы для θ1 и θ2 как функции от времени. Однако возможно выполнить численное интегрирование, используя метод Рунге — Кутты или подобную технику.
Примечания
- Levien RB and Tan SM. Double Pendulum : An experiment in chaos.American Journal of Physics 1993; 61 (11) : 1038