Гекс
Гекс — математическая игра на ромбической доске, имеющей гексагональную сетку.
| Гекс | |
|---|---|
 Игра гекс, выпускаемая фирмой «Паркер бразерс» в 1950-х годах | |
| Игроков | 2 |
| Возраст | 4+ |
| Подготовка к игре | 1 мин |
| Длительность партии | 15 мин (для доски 11×11) |
| Сложность правил | низкая |
| Уровень стратегии | высокий |
| Влияние случайности | нет |
| Развивает навыки | тактика, стратегия |
История игры
История создания игры интересна: её придумали независимо друг от друга 2 человека, правда с разрывом в несколько лет — Пит Хейн в Дании (1942) и Джон Нэш в США (1948)[1][2].
В 1942 году Пит Хейн размышлял над проблемой четырёх красок и ему пришла в голову идея игры в гекс. Идея игры так его увлекла, что Пит Хейн рассказал о ней своим слушателям во время лекции. Игра заинтересовала не только автора, и вскоре её правила опубликовала газета «Политикен».
Постепенно гекс стал очень популярным в Дании. Гекс в то время называли «Многоугольники» и играли в эту игру ещё не на досках, а на бумаге. Для того чтобы облегчить создание игрового поля, многие фирмы стали изготавливать специальные блокноты для игры с заранее напечатанными изображениями досок и продавать их любителям игры. Кроме того стали появляться специальные задачи, посвящённые игре, в том числе этюды, похожие на шахматные. Задачи регулярно публиковали в газете «Политикен», лучшие решения премировались. В 1950-х годах эту игру стала выпускать фирма «Паркер бразерс» (англ. Parker Brothers), тогда же игра получила своё нынешнее название — гекс[2].
Правила игры
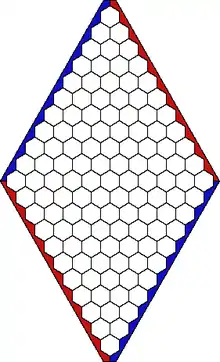
- В гекс играют на специальной доске, которая состоит из шестиугольных полей. Доска может быть любого размера и различных форм, но традиционно используют доску в форме ромба размера n×n, чаще всего 11×11; другие популярные размеры доски 14×14 и 19×19. Джон Нэш, один из изобретателей игры, согласно биографической книге «Игры разума» Сильвии Назар, считал оптимальным размер доски 14×14. На ромбической доске каждое поле в центре доски граничит с шестью соседними полями, поля на сторонах доски имеют четверых соседей, угловые поля граничат с 2 или 3 полями (см. рисунок).
- Один из игроков играет красными фишками (или по-другому камнями), другой — синими (другие варианты раскраски фишек — чёрные и белые, синие и жёлтые, и т. д.). Каждый игрок поочерёдно ставит фишку своего цвета на любое свободное поле. Начинают синие.
- Две противоположные стороны доски окрашены в красный и синий цвета, и называются соответственно красной и синей сторонами. Поля на углах доски относятся к обеим сторонам. Для того чтобы выиграть, игрок должен выстроить цепь из своих фишек, соединив ею стороны своего цвета, то есть красные стремятся построить цепь из красных фишек между двумя красными сторонами доски, а синие — цепь из синих фишек между синими сторонами.
У первого игрока всегда есть победная стратегия, так как лишний ход не может помешать построить цепь[1][2][3]. Для уравнивания шансов используется «Правило пирога», которое позволяет второму игроку сменить цвет сразу после того, как первый игрок делает свой первый ход. При игре с «правилом пирога» выигрышная стратегия есть у второго игрока.
Нетрудно заметить, что игра никогда не кончается вничью, а цели игроков взаимоисключают друг друга.
Варианты
Игра Y
Y (англ. Y (game)) является одним из обобщений игры Гекс, в которой используется треугольная доска. Целью игры является построение цепочки из своих камней, соединяющей три стороны. Также, как и в Гексе, в игре Y не существует ничейных ситуаций.
Гаванна
Игра Гаванна, придумана Кристианом Фрилингом (Christian Freeling) в 1976 г., относится к тому же классу игр, что и Гекс, однако в Гаванне используется шестиугольная доска и существует несколько выигрышных формирований: кольцо (замкнутая цепочка из камней своего цвета), мост (цепочка, соединяющая две любые угловые клетки доски) или вилка (цепочка, соединяющая три стороны доски).
Пекс
Игра Пекс практически идентична Гексу. Главное (и единственное) отличие заключается в том, что вместо доски, разбитой на шестиугольники, в Пексе используется доска, разбитая на пятиугольники неправильной формы. Примечательное качество подобной доски заключается в том, что одна половина клеток имеет по пять «соседей» а другая — семь «соседей». Это качество используется в уникальных тактических ходах, не существующих в Гексе[4].
Атолл
Атолл является ещё одним из обобщений игры Гекс, в которой используется доска специальной формы. В отличие от доски Гекса, периметр которой включает в себя четыре «острова» (два красных и два синих), периметр доски, используемой в игре Атолл, разбит на большее количество «островов». Цель игры Атолл совпадает с целью игры Гекс — построить цепочку из камней своего цвета, соединяющую два противоположных «острова» того же цвета. В отличие от Гекса, выигрышная цепочка может состоять из нескольких частей, соединяющих каждый из противоположных «островов» с промежуточными «островами»[5].
Некс
В игре Некс помимо камней красного и синего цвета используются также камни нейтрального цвета (то есть не принадлежащего ни одному из игроков). Существует два варианта хода: положить один камень своего цвета и один камень нейтрального цвета или заменить два нейтральных камня на доске на свои камни и заменить один из своих камней на нейтральный камень[6].
См. также
Примечания
- Дэвид А. Кларнер. Математический цветник. Сборник статей и задач = The Mathematical Gardner / Пер. с англ. Ю. А. Данилова; под ред., с предисл. и прилож. И. М. Яглома. — М.: Мир, 1983. — С. 41—44. — 494 с.
- Мартин Гарднер. Математические головоломки и развлечения = Mathematical Puzzles and Diversions / Пер. Ю. А. Данилова, под ред. Я. А. Смородинского. — 2-е. — М.: Мир, 1999. — С. 66—73. — 447 с. — ISBN 5-03-003340-8.
- Winning Ways III, 2003, pp. 743-744.
- История и правила игры Пекс с иллюстрацией, показывающей форму доски
- Правила игры Атолл с иллюстрацией, показывающей форму доски
- Правила игры Некс
Литература
- Elwyn R. Berlekamp, John H. Conway, Richard K. Guy. Winning Ways for Your Mathematical Plays (англ.). — 2nd ed. — A K Peters, 2003. — Vol. 3. — ISBN 1-56881-143-8.
