Вероятность безотказной работы

Среднее время безотказной работы (средняя наработка на отказ) ${\displaystyle T_{0}}$ — для невосстанавливаемых (неремонтируемых) систем — это математическое ожидание времени работы системы до отказа:

${\displaystyle T_{0}=M=\int \limits _{0}^{\mathcal {\infty }}t\cdot f(t)dt=-\int \limits _{0}^{\mathcal {\infty }}tdP(t)}$

Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным; ${\displaystyle f(t)}$ — есть плотность вероятности возникновения отказов системы или её невосстанавливаемого элемента. ${\displaystyle P(T)}$ — есть вероятность безотказной работы в интервале времени ${\displaystyle 0<t<T}$. В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность ${\displaystyle P(T)}$ равна нулю. Вероятность ${\displaystyle P(T)}$ связана с плотностью вероятности возникновения отказов системы или её невосстанавливаемого элемента следующим образом:

${\displaystyle f(t)=-{\frac {dP(t)}{dt}}}$.

Проинтегрировав выражение для ${\displaystyle T_{0}}$ по частям, получим:

${\displaystyle T_{0}=\int \limits _{0}^{\mathcal {\infty }}P(t)dt}$

Графически полученное выражение для ${\displaystyle T_{0}}$ представлено на рисунке как площадь под графиком вероятности безотказной работы Р(T) от времени T. В начальный момент вероятность Р(T) равна единице. В конце времени работы системы вероятность P(T) равна нулю.

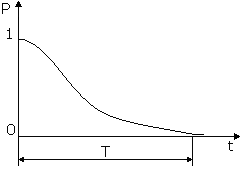
Здесь ${\displaystyle T\geq 0}$ — случайное время работы системы до отказа или наработка на отказ для невосстанавливаемого элемента или системы.

• Экспоненциальное распределение: ${\displaystyle f(t)=\lambda e^{-\lambda t}}$, ${\displaystyle \lambda >0}$, ${\displaystyle t\geqslant 0}$.
• Гамма-распределение: ${\displaystyle f(t)={\frac {\lambda (\lambda t)^{\alpha -1}e^{-\lambda t}}{\Gamma (\alpha )}}}$, ${\displaystyle \lambda ,\alpha >0}$, ${\displaystyle t\geqslant 0}$.
• Распределение Вейбулла: ${\displaystyle f(t)=\lambda \alpha t^{\alpha -1}e^{-\lambda t^{\alpha }}}$, ${\displaystyle \lambda ,\alpha >0}$, ${\displaystyle t\geqslant 0}$.
• Модифицированное распределение экстремального значения: ${\displaystyle f(t)={\frac {1}{\lambda }}\exp {\left[-{\frac {e^{t}-1}{\lambda }}+t\right]}}$, ${\displaystyle \lambda >0}$, ${\displaystyle t\geqslant 0}$.
• Усечённое нормальное распределение: ${\displaystyle f(t)={\frac {1}{a\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right]}}$, ${\displaystyle \sigma >0}$, ${\displaystyle -\infty <\mu <\infty }$, ${\displaystyle 0<t<\infty }$.
• Логарифмически-нормальное распределение: ${\displaystyle f(t)={\frac {1}{t\sigma {\sqrt {2\pi }}}}\exp {\left[-{\frac {(\lg {t}-\mu )^{2}}{2\sigma ^{2}}}\right]}}$, ${\displaystyle \sigma >0}$, ${\displaystyle -\infty <\mu <\infty }$, ${\displaystyle t\geqslant 0}$.

• Леликов О. П. Тема 2. Основные понятия и показатели надежности // Основы расчета и проектирования деталей и узлов машин. Конспект лекций по курсу "Детали машин". — М.: Машиностроение, 2002. — С. 8-9. — 440 с. — 2000 экз. — ISBN 5-217-03077-1.

• Расчёт надёжности
• ГОСТ 27.002—89 (В викитеке)
• Вероятность безотказной работы по ГОСТ 27.002-89