Быстрое преобразование Хафа

Быстрое преобразование Хафа (англ. Fast Hough Transform, сокр. БПХ) — модификация преобразования Хафа, позволяющая параметрически идентифицировать прямые (а также с дополнительной модификацией отрезки и четырехугольники) с меньшей вычислительной сложностью за счет использования факта самопересечения рассматриваемых дискретных прямых.

История

Алгоритм впервые был предложен М. Л. Брейди в 1992 году, [1] в дальнейшем переизобретался несколько раз различными авторами. [2][3]

Определение

БПХ-пирамида для изображения

16\times 16

. Для удобства отображения выполнена на примере преимущественно горизонтальной прямой

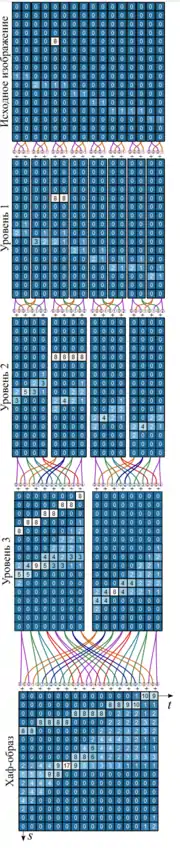
Пусть дано изображение размера $m\times n$ . Рассмотрим $m^{2}$ диадических прямых (прямых специального вида), состоящих из $n$ пикселей на изображении каждая (один пиксель в столбце).

Пусть $I^{(s,t)}(i)$ — интенсивность $i$ -го пикселя, принадлежащего диадической прямой, заданной параметрами $s,t$ ; $S^{(s,t)}$ — Хаф-образ этой диадической прямой.

Образ дискретного преобразование Хафа определяется следующей формулой:

S^{(s,t)}=\sum _{i=0}^{n-1}(I^{(s,t)}(i))

Прямое вычисление всех значений $S^{(s,t)}$ требует $O$ $\left(m^{2}n\right)$ операций: перебор по $m$ различных значений параметров $s$ , $t$ , перебор для каждой пары $n$ значений $i$ .

В свою очередь, алгоритм БПХ, основанный на учете пересечений отрезков друг с другом, требует $\Theta$ $\left(mn\log m\right)$ действий, на одну прямую необходимо $\Theta$ $\left({\frac {n\log m}{m}}\right)$ операций (для квадратных изображений $\Theta$ $\left(\log n\right)$ ). По теореме, сформулированной Т. М. Ханиповым, [4] невозможно сложить диадические прямые с асимптотически меньшей вычислительной сложностью.

Алгоритм

Алгоритм основан на принципе "разделяй и властвуй". Задача состоит в нахождении сумм значений пикселей вдоль отрезков, соединяющих "левый" и "правый" края изображения. Изображение делится пополам, в каждой части задача решается независимо. Для получения итоговой суммы на каждом из отрезков складываются ответы на "левой" и "правой" его половинах.

В алгоритме БПХ пиксели прямых произвольного вида дискретно приближаются диадическими прямыми. Пиксели диадического приближения прямой на изображении размера $n\times n$ удалены от исходной прямой не более, чем на $O$ $(\log n)$ пикселей.[5]

Отрезки параметризуются центрами соединяемых пикселей. Поэтому разбиение отрезка на подотрезки лишь приближенно составляет исходный отрезок. Ошибка аппроксимации с шагами рекурсии накапливается, однако не более чем на $O$ $(\log n)$ пикселей.[5] Построенная таким образом дискретизация отрезка до пикселей называется диадической аппроксимацией.

Порождающие диадические паттерны

Диадические паттерны длины 8 отклонения от 0 до 7. Построение паттернов рекурсивно, поэтому все части длины 2 или 4 совпадают между собой

Далее паттерном называется множество пикселей $p=\{(x_{i},i)\}_{i=0}^{2^{k}-1}$ , содержащее по элементу в каждой вертикали изображения. Отклонением паттерна будет называться значение $t(p)=x_{2^{k}-1}-x_{0}$ , а координатой — значение $s(p)=x_{0}$ . Сдвигом паттерна будет называться множество

p\nearrow (a,b)=\lbrace \left(x_{i}+a,y_{i}+b\right)\ |\ (x_{i},y_{i})\in p\rbrace

Порождающие диадические паттерны ширины $2^{k}$ и наклона $t<2^{k}$ определяются рекурсивно. При $k=t=0$ паттерн состоит из одного пикселя, а при $k>0$ выражается через $k-1$ .

$P_{t}^{k}={\begin{cases}\{(0,0)\}&,k=0\\\ P_{t/2}^{k-1}\ \ \ \cup \ P_{t/2}^{k-1}\ \ \ \ \nearrow (t/2,2^{k})&,k>0,\ \ t\equiv 0\ (mod2)\\P_{(t-1)/2}^{k-1}\cup \ P_{(t-1)/2}^{k-1}\nearrow ((t+1)/2,2^{k})&,k>0,\ \ t\equiv 1\ (mod2)\end{cases}}$

Диадические прямые

Преимущественно горизонтальные, направленные вверх, диадические прямые получаются из всех сдвинутых по вертикали порождающих паттернов $P_{s,t}^{k}=P_{t}^{k}\nearrow (s,0)$ , построенных со всеми возможными координатами на изображении $s\in \{0,...,2^{k}-1\},t\in \{0,...,2^{k}-1\}$ .

Для приближенного вычисления преобразования Хафа требуется найти суммы $S_{s,t}=\sum _{(x,y)\in P_{s,t}^{k}}I_{x,y}$ по всем диадическим прямым на изображении. В этой сумме $2^{k}\cdot 2^{k}$ прямых по $2^{k}$ точек каждая. За счет рекурсивного перехода это суммирование сводится к подсчету отдельно левых, отдельно правых половин, что позволяет свести вычисление к подсчету $2\cdot 2^{k}\cdot 2^{k-1}$ сумм по $2^{k-1}$ точек каждая.

Рассмотрим бинарные слова, состоящие из чисел 0 и 1. Множество диадических слов определяется рекурсивно. $w$ будет называться диадическим словом, если $w$ имеет вид $a0a$ или $a1a$ , где $a$ — пустое или диадическое слово. Все диадические слова длины не больше трех: 0, 1, 000, 010, 101, 111.

Для каждого диадического слова ${\overline {b_{1}b_{2}...b_{n}}}$ рассматривается кумулятивная сумма $\{a_{i}\}_{0}^{2^{k}-1},a_{i}=\sum _{0}^{i}b_{i}$ . Будем говорить, что последовательность пикселей $\{(a_{i},i)\}_{0}^{2^{k}-1}$ — диадическая прямая, соединяющая центры пикселей $(0,0)$ и $(a_{2^{k}-1},2^{k}-1)$ .

Существует ровно $2^{k}$ диадических прямых длины $2^{k}$ . По одной на каждую пару $(0,0)$ и $(h,2^{k}-1),0\leqslant h<2^{k}$ .

Формальное описание

Алгоритм БПХ устроен следующим образом:[6]

Исходное состояние матрицы — исходное изображение размера $2^{p}\times 2^{q}$ . Затем происходит вычисление на $q-1$ -их уровнях по очереди, начиная с первого: на $i$ -том уровне матрица в текущем состоянии делится на группы по принципу равенства целой части координаты второй оси после деления на $2^{i}$ ; получаются подматрицы $2^{p}\times 2^{i}$ ; объединим соседние в пары (без пересечений, это возможно, так как размер матрицы — степень двойки) и назовем в этой паре первой ту подматрицу, что расположена на меньших координатах по второй координате в матрице,а другую — второй; вместо первых в каждой паре записывается ее сумма с соответствующей ей второй, а вместо второй — сумму первой и второй с циклическим сдвигом на один влево. Таким образом считается Хаф-образ таких прямых, что для любой пары точек с координатами $(x_{1},y_{1}),(x_{2},y_{2})$ с этой прямой выполняется $(x_{1}\neq x_{2})\rightarrow ((y_{1}\neq y_{2})\wedge (x_{1}<x_{2}\Leftrightarrow y_{1}<y_{2}))$ , с помощью аппроксимации диадическими прямыми. Для того, чтобы посчитать образ для остальных прямых, достаточно поворачивать изображение и проводить ту же самую операцию, а полученные результаты сложить.

Полученные таким образом на каждом уровне матрицы являются элементами БПХ-пирамиды. Формальное описание БПХ-пирамиды: Нулевым уровнем БПХ-пирамиды является исходное изображение (размером $m\times n$ , а последним – Хаф-образ, содержащий суммы по диадическим прямым длины $n=2^{p}$ . Для описания $q$ -ого уровня пирамиды исходное изображение разбивается на горизонтальные полосы $[0,n-1]\times [k\cdot 2^{q},(k+1)\cdot 2^{q}-1]$ , где $k$ - номер полосы, $k\in [0,2^{p-q}-1]$ . Для каждой полосы в $q$ -ом уровне БПХ-пирамиды хранятся суммы по всевозможным паттернам полосы, имеющим длину $2^{q}$ и параметры $s\in [0,n-1],t\in [0,2^{q}-1]$ . Количество таких паттернов для полосы – $n\cdot 2^{q}$ , поэтому $q$ -й уровень пирамиды занимает столько же памяти, сколько исходное изображение.

Инвариантность количества затрачиваемой памяти и возможность хранить каждый уровень в матрице того же размера, что оригинальное изображение, без потери интерпретируемости дает следующее свойство: можно хранить БПХ-пирамиду в форме матрицы с размерностью, на одну большую, чем размерность исходного изображения (по одной оси - количество уровней, $\log _{2}n$ ), по остальным - размер изображения).[7]

Программные реализации

Пример реализации на языке python:

import numpy as np
W = 2**5
H = 2**5
img = np.random.random([H, W])

def calc_sums(img, xmin, xmax):
    res = np.zeros([W, xmax-xmin])
    if xmax - xmin == 1:
        res[:, 0] = img[:, xmin]
    else:
        mid = (xmin + xmax) // 2
        ans1 = calc_sums(img, xmin, mid)
        ans2 = calc_sums(img, mid, xmax)
        for x in range(W):
            for shift in range(xmax-xmin):
                res[x, shift] = ans1[x, shift//2] + ans2[(x + shift//2 + shift%2) % W, shift//2]
    return res
res = calc_sums(img, 0, W)

Алгоритм реализован в библиотеке opencv[8] и может быть использован, например, для быстрого нахождения точки схода.[9]

Обобщения на трехмерный случай

БПХ для плоскостей

Решение этой задачи подразумевает использование алгоритма для двумерного случая.

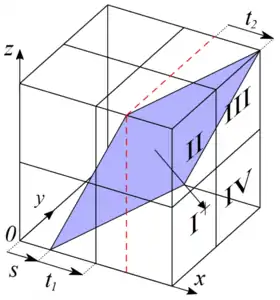
Типизация плоскостей в пространстве

Хаф-образ плоскостей будет так же трехмерным (плоскость задается через три координаты вектора, перпендикулярного ей). Пусть он будет задан параметризацией $s,t,t_{2}$ , где $s$ — координата $x$ пересечения плоскости с границей изображения на луче $Ox$ , $s+t$ — координата $x$ точки пересечения с границей изображения, параллельной лучу $Ox$ в плоскости $xOz$ , $t_{2}$ — разница координат $x$ второй и первой точки пересечения плоскости с границами изображения. Первая точка находится в пересечении содержащих границу изображения плоскостей $xOz$ и плоскости, параллельной $xOy$ . Вторая точка - в пересечении содержащих границу изображения плоскостей, параллельных $xOy$ и $xOz$ .

Будем называть плоскость преимущественно-перпендикулярной к оси координат, если нормаль к ней образует с данной осью меньший угол, чем с двумя другими. Будем рассматривать только плоскости, преимущественно-перпендикулярные к оси y. Они разделяются на 4 типа наклонов, как это показано на рисунке 4. Без ограничения общности будем считать, что рассматриваемые плоскости имеют тип I.

Построение Хаф-образа методом перебора плоскостей имеет асимптотическую сложность $O$ $\left(mnk\cdot (mn+nk+mk)\right)$ (количество плоскостей, умноженное на количество операций для суммирования одной плоскости), где m, n, k — размеры изображения в каждой размерности.

Быстрым преобразованием Хафа в данном случае будет следующий алгоритм:

Для каждой плоскости перпендикулярной оси $Oz$ с координатой $z$ по этой оси считается быстрое преобразование Хафа, а результат кладется в трехмерное пространство по координатам $s,t,z$ .
Для каждой плоскости в получившемся трехмерном пространстве перпендикулярной оси $Ot$ с координатой $t$ по этой оси считается быстрое преобразование Хафа, а результат кладется в куб по координатам $s,t,t_{2}$ .

Сложность такого преобразования складывается из сложности первого шага ( $\Theta$ $\left(k\cdot mn\log m\right)$ ) и сложности второго шага ( $\Theta$ $\left(n\cdot mk\log m\right)$ ), которые считаются, как произведение количества рассматриваемых плоскостей и количества операций на одну плоскость. Итого, $\Theta$ $\left(mnk\log m\right)$ , в пересчете на одну плоскость $\Theta$ $(\log m)$ .

БПХ для трехмерных прямых

Хаф-образ трехмерной прямой будет четырехмерным (по два параметра на каждую из двух точек на прямой). Пусть он будет задан параметризацией $s,t,s_{2},t_{2}$ . $s,s_{2}$ — координаты x, y точки на плоскости $xOy$ , $s+t,s_{2}+t_{2}$ — координаты x, y точки пересечения прямой с границей изображения, параллельной плоскости $xOy$ .

Построение Хаф-образа методом перебора трехмерных прямых имеет асимптотическую сложность $O$ $\left((mn)^{2}\cdot k\right)$ (количество прямых умноженное на количество операций для суммирования одной прямой), где m, n, k — размеры изображения в каждой размерности.

Быстрое преобразование Хафа для такого случая формулируется подобно определению для двумерного случая. В двумерном случае возможность сдвига была только вдоль одной оси, теперь же сдвиг будет вдоль одной оси, вдоль второй оси и вдоль двух осей одновременно.

Подсчет паттернов длины два требует ${\frac {k}{2}}$ (количество групп суммируемых плоскостей), умноженное на $4mn$ (сложность проводимых сложений для каждой группы), операций. Подсчет паттернов длины 4 требует ${\frac {k}{4}}\cdot 16mn$ операций. Длины паттернов $d$ — ${\frac {k}{d}}\cdot d^{2}mn=mnkd=mnk\cdot 2^{i}$ , где $i$ определяется, как $\log _{2}(d)$ , то есть номер рассматриваемой длины паттерна. Суммируя $\log _{2}(k)$ слагаемых (количество возможных для рассматриваемого изображения длин паттернов) с использованием формулы суммы геометрической прогрессии, получается сложность алгоритма $\Theta$ $\left(\sum _{i=1}^{\log _{2}k}mnk\cdot 2^{i}\right)\equiv$ $\Theta$ $\left({\frac {2mnk\cdot (2^{\log _{2}k}-1)}{2-1}}\right)\equiv$ $\Theta$ $\left(mnk^{2}\right)$ , а сложность на одну прямую $\Theta$ $\left({\frac {k^{2}}{mn}}\right)$ . При $m=n=k$ сложность будет константной.

Сочетание БПХ и принципа четырех русских

Несмотря на то, что количество операций на одну прямую константное при равном размере изображения в каждой размерности, для всех прямых надо потратить $n^{4}$ . Но если не нужны все прямые,а нужна только часть их, то можно совершить предпосчет первых $x$ шагов [10] , сохранить их в память, а затем посчитать суммы только для тех прямых, которые нужны.

Этот концепт был закреплен в методе четырех русских. Метод назван в честь первоткрывателей В. Арлазаров, М. Кронрод, Е. Диниц, И. Фараджев.

В оригинальном алгоритме БПХ для трехмерных прямых совершается на каждом из $\log _{2}k$ уровней подсчет для прямых определенной длины. С другой стороны можно сделать предпосчет только для первых $x$ шагов, а затем производить подсчет для нужных прямых.

Для того, чтобы определить оптимальное количество шагов предпосчета, необходимо решить такое уравнение ( $a$ — количество прямых, которое необходимо найти алгоритму):

$\Theta \left(mnk2^{x}\right)=\Theta \left(a2^{\log _{2}k-x}\right)$

Слева — количество операций для выполнения предпосчета. Справа — количество операций на нахождение сумм вдоль запрошенных прямых. Пусть необходимо найти все прямые, тогда $a=mnk$ , тогда решением уравнения будет $x={\frac {1}{2}}\log _{2}k=\log _{2}{\sqrt {k}}$ , а левая и правая части равны $\Theta \left(mnk{\sqrt {k}}\right)$ , что в ${\sqrt {k}}$ меньше, чем без предпосчета. Тем не менее за уменьшение количества операций необходимо заплатить памятью в том же размере, что занимает Хаф-образ (свойство инвариантности занимаемой памяти на каждом уровне подсчета алгоритмом БПХ).

Вычисление суммы по отрезку на изображении

Принцип вычисления основан на использовании значений не только последнего уровня БПХ-пирамиды (то есть непосредственно самого Хаф-образа), но и других уровней БПХ-пирамиды.

Задача делится на две подзадачи:

Найти диадическую прямую проходящую через два заданных пикселя
Из суммы значений вдоль этой прямой выделить ту часть суммы, которая относится к паттерну между заданными пикселями

Поиск диадической прямой проходящей через два заданных пикселя

Без ограничения общности считаем, что $y_{2}\geq y_{1}$ . Здесь будут рассмотрены только преимущественно вертикальные паттерны с наклоном вправо, то есть $x_{2}\geq x_{1}$ и $y_{2}-y_{1}\geq x_{2}-x_{1}$ . Также используется $(s,t)$ -параметризация и значение $p$ равное $\log _{2}n$ , где $n$ - размер изображения по оси $y$ .

Пусть двоичное разложение параметра $t$ диадической прямой выглядит как $t=\sum _{i=0}^{p-1}t_{i}2^{i}$ Тогда паттерн может быть записан так ( $\left[\cdot \right]$ - округление до ближайшего целого.):

$x=s+\sum _{r=0}^{p-1}t_{r}\left[{\frac {s^{r}y}{2^{p}-1}}\right]$

$\Delta x=x_{2}-x_{1}$ считается из данных задачи. $\delta _{r}^{y_{1},y_{2}}=\left(D_{r}(y_{2})-D_{r}(y_{1})\right)$ - число сдвигов рассматриваемого паттерна в полосе $(y_{1},y_{2})$ , которое также известно. Таким образом необходимо только восстановить биты $t_{0},t_{1},\ldots ,t_{p-1}$ .

Для восстановления используется "жадный" алгоритм: Все биты $t_{r}$ сначала равны нулю. Так как $i>j\rightarrow \delta _{i}^{y_{1},y_{2}}\geq \delta _{j}^{y_{1},y_{2}}$ , поэтому перебор ведется от большего числа сдвигов к меньшему, от уровня $p-1$ до уровня 0. Если $\Delta y\geq \delta _{r}^{y_{1},y_{2}}$ , то соответствующий этому уровню бит устанавливается в 1, а $\Delta y$ уменьшается на $\delta _{r}^{y_{1},y_{2}}$ . Шаг повторяется, пока $\Delta y$ не обратится в 0.

По $t_{i}$ вычисляется значение параметра $t$ . Через этот параметр вычисляется параметр $s$ по следующей формуле:

$s=D(y_{1},t)-\sum _{r=0}^{p-1}t_{r}D_{r}(y_{1})$

$\#\lbrace \delta _{r}^{y_{1},y_{2}}\rbrace =p=\log _{2}n$ , поэтому сложность алгоритма $\Theta$ $(\log n)$ .[7]

Способ 1

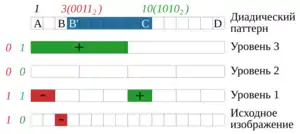
Пример получения произвольного отрезка диадической прямой

Обращаясь к рисунку, можно увидеть, что произвольный отрезок на прямой длины $n$ вычисляется, нахождением минимального количества диадических паттернов, в которых содержатся части от начала прямой до конца заданного отрезка включительно, и минимальное количество паттернов, которые содержат отрезок от начала прямой до начала заданного отрезка, исключая первый пиксель исходного отрезка. То есть нужно найти суммы для двух отрезков с началом на границе изображения и разными координатами конца.

Для подсчета суммы по такого типа отрезка длины $l$ (его двоичное разложение $\sum _{j=0}^{p}\left(l_{j}\cdot 2^{j}\right)$ ) $\sum _{q=0}^{p}\left[l_{q}\cdot H^{s,t}\left(q,\sum _{j=q+1}^{p}l_{j}\cdot 2^{j-q}\right)\right]$ , где $H^{s,t}\left(q,k\right)$ - сумма по паттерну $2^{q}$ в $k$ -ой полосе $q$ -ого уровня БПХ=пирамиды для прямой с параметрами $(s,t)$ .

Внутренняя сумма не требует полного вычисления на каждом шаге, поскольку получается из предыдущей за константное время. Таким образом, трудоемкость алгоритма пропорциональна числу слагаемых во внешней сумме, т.е. составляет $\Theta$ $(\log n)$ . Так как результат вычисляется для двух отрезков этого типа, то результирующая сложность алгоритма так же $\Theta$ $(\log n)$ . Причем стоит заметить, что пиксель может быть многоканальным.[7]

Способ 2

Отрезок может быть составлен из минимального количества паттернов внутри отрезка. Для поиска таких паттернов нужно смотреть уровни БПХ-пирамиды, начиная с последних и заканчивая первыми. Сразу можно отсеять те паттерны, которые не входят в отрезок. Если попадается паттерн полностью лежащий внутри отрезка, то его сумма включается в искомую сумму, а его разбиения на следующих уровнях не рассматриваются. Этот способ более вычислительно сложный, чем первый, так как требует перебора всех паттернов, которых более $n$ .

Вычисление суммы по четырехугольнику на изображении

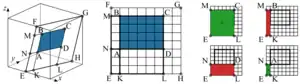
Пример получения дискретного четырехугольника произвольного положения

Аналогично вычислению суммы по отрезку для вычисления суммы по четырехугольнику из промежуточных вычислений Хаф-образа для плоскостей, иначе говоря БПХ-пирамидой для случая плоскостей.

Предполагая, что параметры $(s,t,t_{2})$ плоскости на которой находится заданный четырехугольник известны, искомая сумма вычисляется по формуле включения-исключения беря сумму по четырем прямоугольникам, одна вершина которых — угловая вершина диадической плоскости (обозначим ее буквой $E$ , а сегменты с этой вершиной угловыми сегментами). Обозначим координаты точек ближней и дальней от $E$ вершин заданного четырехугольника через $(i_{1},j_{1})$ и $(i_{2},j_{2})$ соответственно. Суммы обозначенных угловых сегментов с вершинами в $(i_{1}-1,j_{1}-1)$ и $(i_{2},j_{2})$ берутся со знаком плюс, а суммы тех, что с вершинами в $(i_{1}-1,j_{2})$ и $(i_{2},j_{1}-1)$ , берутся со знаком минус.

Чтобы найти сумму по произвольному угловому сегменту, необходимо разбить его на сегменты, присутствующие в БПХ-пирамиде. Необходимо рассмотреть двоичные разложения ширины и высоты сегмента. Аналогично одномерному случаю сегмент разбивается по горизонтали на $\log _{2}n$ вертикальных полос и по вертикали не более чем на $\log _{2}n$ горизонтальных полос. Их пересечение даст не более чем $\log _{2}n$ сегментов, присутствующих в трехмерной БПХ-пирамиде. Таким образом, сложность вычисления суммы по произвольному сегменту составляет $\Theta$ $(\log n)$ операций.[7]

Применения алгоритма БПХ

Хотя у апроксимации прямой диадическим паттерном есть некоторая ошибка, впрочем эксперименты показывают, что это ошибка достаточно незначительна для того, чтобы в решениях задач можно было заменить традиционный алгоритм преобразования Хафа на алгоритм БПХ.[11]

Робастное решение задачи линейной регрессии путем вычисления M-оценок с помощью БПХ

Применяя М-оценки к задаче линейной регрессии, можно получить радиально-базисные функции. Они составляют "непрерывное" изображение, которое в свою очередь дискретизуется в двумерную гистограмму.

Далее выполняеncя свёртка изображения с дискретизованным ядром $K$ , соответствующим выбранной М-оценке. На основе полученного вычисляется Хаф-образ с помощью БПХ. Координата максимума в пространстве параметров - и будет являться искомой М-оценкой.

Быстрая линейная бинарная кластеризация

Задача формулируется следующим образом: необходимо найти гиперплоскость, которая разделяет изображение на 2 класса. Изображение представляется в виде нормированной гистограммы изображения $P$ .

$L$ — искомая гиперплоскость, делящая изображения на два класса $A_{L},B_{L}$ , $\Omega$ — класс всех элементов гистограмммы.

Используемые аддитивные статистики $X\subset \Omega$ ( $x_{i}$ - $i$ -ая координата $x$ ):

$D^{0}(X)=\sum _{x\in X}P(x)$
$D_{i}^{1}(X)=\sum _{x\in X}x_{i}P(x)$
$D_{ij}^{2}(X)=\sum _{x\in X}x_{i}x_{j}P(x)$

Существует ряд функционалов, подходящих для задач разделения кластеров с разными априорно известными свойствами, и при этом вычислимых через аддитивные статистики. Стоит еще раз упомянуть, что эти функционалы в общем случае не выпуклы и единственным надежным способом отыскания их оптимального значения является полный перебор на сетке в пространстве параметров разделяющих поверхностей.

Наивный алгоритм: Существует $O(n^{2})$ дискретных прямых, пересекающих гистограмму с линейным размером $n$ . Для каждой из них требуется выполнить $O(n^{2})$ операций по вычислению весов, матриц ковариации и, наконец, значений критерия. Таким образом, вычислительная сложность наивного алгоритма составляет $O(n^{4})$ операций. Аналогично можно показать, что для трехмерного случая вычислительная сложность алгоритма будет составлять $O(n^{6})$ .

На этом этапе применяется кумулятивное суммирование: в элемент слоя с номером $i$ выходного изображения записывается сумма соответствующих элементов всех слоев входного изображения с индексом, не превосходящим $i$ .

Сумма значений пикселей по любой строке выходного изображения равна сумме по той части исходного изображения, что располагается не ниже этой строки. Более того, сумма вдоль любой преимущественно горизонтальной прямой на выходном изображении равна сумме по ограничиваемой ею верхней полуплоскости на исходном изображении. Для аналогичного выражения сумм по левым полуплоскостям через преимущественно вертикальные прямые нужно вместо вертикальной выполнить горизонтальную кумулятивную сумму изображения.

Алгоритм:

вычислим набор изображений, содержащих значения необходимых аддитивных статистик для каждого из элементов входной гистограммы ( $D^{0},D_{i}^{1},D_{ij}^{2}$ ) (6 в двумерном случае, 10 в трехмерном)
вычисление кумулятивной суммы вдоль каждой из осей, получим кортеж изображений. Для любого изображения этого кортежа, относящегося к размерности $d$ , сумма по любой гиперплоскости, преимущественно перпендикулярной оси с индексом $d$ , равна соответствующей аддитивной статистике, вычисленной по полупространству, включающему начало координат и ограниченному выбранной гиперплоскостью. Зная значение аддитивной статистики для одного полупространства, легко получить значение той же статистики и для второго – вычитанием из статистики, посчитанной по всему изображению.
теперь, вычислив аддитивные статистики по всем разделениям гиперплоскостей, можно считать значения критерия для выбора оптимальной кластеризации.

Если просто суммировать по всем гиперплоскостям то в двумерном случае сложность $O(mn^{3})$ , в трехмерном $O(mn^{5})$ . (В $k$ -мерном $O(mn^{2k-1})$ )

Суммирование по гиперплоскостям (прямым в двумерном случае, плоскостям в трехмерном…) можно сделать с помощью БПХ. Это помогает снизить сложность с $O(n^{2k-1})$ до $O(n^{k}\log {\left(n\right)})$ для каждого из $m$ изображений. Т.е. теперь сложность в двумерном случае $O(mn^{2}\log {\left(n\right)})$ , в трехмерном $O(mn^{3}\log {\left(n\right)})$ .

Таким образом, финальный алгоритм:

Кумулятивная суммация
Подсчет аддитивных статистик
БПХ
Поиск максимума в пространстве Хафа

Сложность: время $O(mn^{k}\log {\left(n\right)})$ , память $O(mn^{k})$ .

В двумерном случае более подробно:

Кумулятивная суммация: $O(n^{2})$
Подготовка к вычислению аддитивных статистик: $O(n^{2})$
БПХ: $O\left(n^{2}\log {\left(n\right)}\right)$
Поиск максимума в пространстве Хафа: $O(n^{2})$

Итоговая сложность: $O(n^{2}\log {\left(n\right)})$

В трехмерном случае более подробно:

Кумулятивная суммация: $O(n^{3})$
Подготовка к вычислению аддитивных статистик: $O(n^{3})$
БПХ: $O\left(n^{3}\log {\left(n\right)}\right)$
Поиск максимума в пространстве Хафа: $O(n^{3})$

Итоговая сложность: $O(n^{3}\log {\left(n\right)})$

Другие применения

Далее представлены только некоторые задачи, которые могут быть решены с использованием преобразования Хафа.

Отслеживание равномерно движущихся объектов, используя покадровую разность изображений. Эти объекты на своих треках оставляют выраженные прямые линии.[12][13]
Детекция точки схода на изображении. Точка схода – это точка на плоскости изображения в которой пересекаются проекции параллельных в трехмерной сцене прямых.[14][15]
Томографическое восстановление. Процедуру формирования проекций изображения анализируемого объекта с использованием рентгеновских лучей принято моделировать преобразованиями Хафа и Радона, а получение трехмерной структуры исследуемого объекта часто сводится к решению обратного преобразования Хафа или Радона.[16]
Анализ медицинских изображений.[17]
В реализации алгоритмов слепой калибровки радиальной дисторсии при условии нахождения прямолинейных объектов на сцене. Через оптимизацию нового функционала Хаф-образа подбираются параметры компенсации радиальной дисторсии.[18]
Определение степени сбития камеры. Основано на подсчете БПХ от эпиполярной картины и поиске прямой, на которой лежат точки интересующих прямых на эпиполярной картине.
Распознавание рукописного текста.[19]
Определение наклона шрифта. Основано на том, что в шрифте есть символы состоящие из прямых отрезков, находящихся под одним углом, вдоль такого угла Хаф-образ будет большее значение.[20]
Распознавание штрих-кодов.[21][22]
Определение степени сходства форм.[23]
Векторизации трехмерных изображения.[24]
Детекция треков спутников по изображениям с длинной выдержкой.[25]
Обнаружение радиолокационных целей.[26][27]
Анализа деформаций подземного профиля.[28]
Анализ структуры топологии микросхем по фотографиям.[29]
Подсчет количества осей транспортного средства по трекам детектора колес изображений, полученных с камеры, снятой сбоку.[30]
Трехмерная реконструкции плоских граней прозрачных минералов по набору изображений.[31]
Анализ SAR снимков.[32]

Примечания

Martin L. Brady, Whanki Yong. Fast Parallel Discrete Approximation Algorithms for the Radon Transform // Proceedings of the Fourth Annual ACM Symposium on Parallel Algorithms and Architectures. — New York, NY, USA: ACM, 1992. — С. 91–99. — ISBN 9780897914833. — doi:10.1145/140901.140911.
J.E. Vuillemin. Fast linear Hough transform // International Conference on Application-Specific Systems, Architectures and Processors, Proceedings. — IEEE, 1994. — ISBN 0-8186-6517-3. — ISSN 1063-6862. — doi:10.1109/ASAP.1994.331821.
С.М. Карпенко , Д.П. Николаев , П.П. Николаев , В.В. Постников. Быстрое преобразование Хафа с управляемой робастностью // Искусственные интеллектуальные системы и Интеллектуальные САПР. Труды международной конференции IEEE AIS"04 и CAD-2004. — Физматлит, 2004. — Т. 2, вып. 2. — С. 303-309.
Timur M. Khanipov. Computational complexity lower bounds of certain discrete Radon transform approximations (англ.). — 2018-01-03.
S. M. Karpenko, E. I. Ershov. Fast Hough Transform and approximation properties of dyadic patterns (англ.). — 2017-12-15.
E. I. Ershov, A. P. Terekhin, D. P. Nikolaev. Generalization of the Fast Hough Transform for Three-Dimensional Images (англ.) // Journal of Communications Technology and Electronics. — 2018-06-01. — Vol. 63, iss. 6. — P. 626–636. — ISSN 1555-6557. — doi:10.1134/S1064226918060074.
K.V. Soshin, D.P. Nikolaev, S.A. Gladilin, E.I. Ershov. Acceleration of Summation Over Segments Using the Fast Hough Transformation Pyramid (англ.) // South Ural State University Mathematical Modelling, Programming & Computer Software : Alevtina V. Keller, Natalia A. Manakova, Georgy A. Svirdyuk, Vladimir I. Zalyapin, Alena A. Zamyshlyaeva. — Chelyabinsk: South Ural State University, 2020. — Т. 13, вып. 1. — С. 129-140. — doi:10.14529/mmp200110.
OpenCV: opencv2/ximgproc/fast_hough_transform.hpp File Reference (неопр.). docs.opencv.org. Дата обращения: 9 мая 2019.
Alexander Krotov. OpenCV Fast Hough Transform example. — 2017-09-05.
Bulatov K. B., Chukalina M. V., Nikolaev D. P. Fast x-ray sum calculation algorithm for computed tomography (англ.) // ЮУрГУ ММП Вестник. — 2020. — Т. 13, вып. 1. — С. 95-106. — doi:10.14529/mmp200107.
Е.И. Ершов. Быстрое преобразование Хафа как инструмент анализа двумерных и трехмерных изображений в задачах поиска прямых и линейной кластеризации (рус.). — 2018.
A. E. Cowart, W. E. Snyder, W. H. Ruedger. The detection of unresolved targets using the Hough transform (рус.) // Computer Vision, Graphics, and Image Processing. — 1983. — Т. 21, вып. 2. — С. 222-238.
A. Mitiche, P. Bouthemy. Computation and analysis of image motion: A synopsis of current problems and methods (англ.) // International journal of computer vision. — 1996. — Vol. 19, iss. 1. — P. 29-55.
E. Lutton, H. Maitre, J. Lopez-Krahe. Contribution to the determination of vanishing points using Hough transform (англ.) // IEEE transactions on pattern analysis and machine intelligence. — 1994. — Vol. 16, iss. 4. — P. 430-438.
D. Nikolaev et al. Hough transform: underestimated tool in the computer vision field (англ.) // Proceedings of the 22th European Conference on Modelling and Simulation. — 2008. — P. 238-246.
V. Prun et al. Effective regularized algebraic reconstruction technique for computed tomography (англ.) // Crystallography Reports. — 2013. — Vol. 58, iss. 7. — P. 1063-1066.
Z.-H. Cho, J. P. Jones, M. Singh. Foundations of medical imaging (рус.). — Wiley New York, 1993.
I. A. Kunina, S. A. Gladilin, D. P. Nikolaev. Blind compensation of radial distortion in a single image using fast Hough transform (англ.) // Computer Optics. — 2016. — Vol. 40, iss. 3. — P. 395-403.
А. Мозговой. Преобразование Хафа в задачах автоматического распознавания рукописного текста (рус.). — 2012. — Вып. 9. — С. 62-64.
E. Limonova, P. Bezmaternykh, D. Nikolaev, V. Arlazarov. Slant Rectiﬁcation in Russian Passport OCR System Using Fast HoughTransform (англ.) // 9-th International Conference on Machine Vision, ICMV 2016. — SPIE, 2017. — P. 103410P. — doi:10.1117/12.2268725.
В. А. Фурсов, С. А. Бибиков, П. Ю. Якимов. Локализация контуров объектов на изображениях при вариациях масштаба с использованием преобразования Хафа (рус.) // Компьютерная оптика. — 2013. — Т. 37, вып. 4.
R. Muniz, L. Junco, A. Otero. A robust software barcode reader using the Hough transform (англ.) // International Conference on Information Intelligence and Systems, 1999. Proceedings.. — IEEE, 1999. — P. 313-319.
А. Рубис и др. Морфологическое сравнение по форме точечных паттернов и контурных изображений на основе преобразования Хафа и его модификаций (рус.) // Вестник компьютерных и информационных технологий. — 2011. — Вып. 7. — С. 9-16.
М. Кудрина [и др.] Векторизация растровых изображений с использованием преобразования Хафа (рус.) // Труды Международного симпозиума "Надежность и качество". — 2013. — Т. 1.
B. Vandame. Fast Hough transform for robust detection of satellite tracks (англ.) // Mining the Sky. — Springer, 2001. — P. 595-597.
А. Семенов. Обнаружение радиолокационных целей с помощью преобразования Хафа (рус.) // Наука и образование: научное издание МГТУ им. НЭ Баумана. — 2014. — Вып. 12.
B. Carlson, E. Evans, S. Wilson. Search radar detection and track with the Hough transform. III. Detection performance with binary integration (англ.) // IEEE transactions on Aerospace and Electronic Systems. — 1994. — Vol. 30, iss. 1. — P. 116-125.
А. Долгий, А. Хатламаджиян. Гибридная модель интерпретации деформаций в балластной призме и основной площадке земляного полотна на основе целевого преобразования Хафа и нейронной сети Кохонена (рус.) // Известия Южного федерального университета. Технические науки. — 2007. — Т. 77, вып. 2.
А. Дудкин, Д. Вершок, А. Селиханович. Выделение контуров на полутоновых изображениях топологических слоев интегральных микросхем (рус.) // Искусственный интеллект. — 2004. — Вып. 3. — С. 453-458.
А. Григорьев, Т. Ханипов, Д. Николаев. Определение количества осей транспортного средства по видеоряду проезда (рус.) // 54-й научной конференции МФТИ. — 2011. — Т. 10. — С. 31.
В. Гаганов, А. Игнатенко, М. Ломоносова. Трехмерная реконструкция плоских граней прозрачных минералов по набору изображений с микроскопа (рус.) // Труды конференции Графикон. — 2008. — С. 227-233.
J. Skingley, A. Rye. The Hough transform applied to SAR images for thin line detection (англ.) // Pattern Recognition Letters. — 1987. — Vol. 6, iss. 1. — P. 61–67.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Martin L. Brady, Whanki Yong. Fast Parallel Discrete Approximation Algorithms for the Radon Transform // Proceedings of the Fourth Annual ACM Symposium on Parallel Algorithms and Architectures. — New York, NY, USA: ACM, 1992. — С. 91–99. — ISBN 9780897914833. — doi:10.1145/140901.140911.

[2] J.E. Vuillemin. Fast linear Hough transform // International Conference on Application-Specific Systems, Architectures and Processors, Proceedings. — IEEE, 1994. — ISBN 0-8186-6517-3. — ISSN 1063-6862. — doi:10.1109/ASAP.1994.331821.

[3] С.М. Карпенко , Д.П. Николаев , П.П. Николаев , В.В. Постников. Быстрое преобразование Хафа с управляемой робастностью // Искусственные интеллектуальные системы и Интеллектуальные САПР. Труды международной конференции IEEE AIS"04 и CAD-2004. — Физматлит, 2004. — Т. 2, вып. 2. — С. 303-309.

[4] Timur M. Khanipov. Computational complexity lower bounds of certain discrete Radon transform approximations (англ.). — 2018-01-03.

[:0-5] S. M. Karpenko, E. I. Ershov. Fast Hough Transform and approximation properties of dyadic patterns (англ.). — 2017-12-15.

[6] E. I. Ershov, A. P. Terekhin, D. P. Nikolaev. Generalization of the Fast Hough Transform for Three-Dimensional Images (англ.) // Journal of Communications Technology and Electronics. — 2018-06-01. — Vol. 63, iss. 6. — P. 626–636. — ISSN 1555-6557. — doi:10.1134/S1064226918060074.

[SummationOverSegmentAcceleration-7] K.V. Soshin, D.P. Nikolaev, S.A. Gladilin, E.I. Ershov. Acceleration of Summation Over Segments Using the Fast Hough Transformation Pyramid (англ.) // South Ural State University Mathematical Modelling, Programming & Computer Software : Alevtina V. Keller, Natalia A. Manakova, Georgy A. Svirdyuk, Vladimir I. Zalyapin, Alena A. Zamyshlyaeva. — Chelyabinsk: South Ural State University, 2020. — Т. 13, вып. 1. — С. 129-140. — doi:10.14529/mmp200110.

[8] OpenCV: opencv2/ximgproc/fast_hough_transform.hpp File Reference (неопр.). docs.opencv.org. Дата обращения: 9 мая 2019.

[9] Alexander Krotov. OpenCV Fast Hough Transform example. — 2017-09-05.

[10] Bulatov K. B., Chukalina M. V., Nikolaev D. P. Fast x-ray sum calculation algorithm for computed tomography (англ.) // ЮУрГУ ММП Вестник. — 2020. — Т. 13, вып. 1. — С. 95-106. — doi:10.14529/mmp200107.

[11] Е.И. Ершов. Быстрое преобразование Хафа как инструмент анализа двумерных и трехмерных изображений в задачах поиска прямых и линейной кластеризации (рус.). — 2018.

[12] A. E. Cowart, W. E. Snyder, W. H. Ruedger. The detection of unresolved targets using the Hough transform (рус.) // Computer Vision, Graphics, and Image Processing. — 1983. — Т. 21, вып. 2. — С. 222-238.

[13] A. Mitiche, P. Bouthemy. Computation and analysis of image motion: A synopsis of current problems and methods (англ.) // International journal of computer vision. — 1996. — Vol. 19, iss. 1. — P. 29-55.

[14] E. Lutton, H. Maitre, J. Lopez-Krahe. Contribution to the determination of vanishing points using Hough transform (англ.) // IEEE transactions on pattern analysis and machine intelligence. — 1994. — Vol. 16, iss. 4. — P. 430-438.

[15] D. Nikolaev et al. Hough transform: underestimated tool in the computer vision field (англ.) // Proceedings of the 22th European Conference on Modelling and Simulation. — 2008. — P. 238-246.

[16] V. Prun et al. Effective regularized algebraic reconstruction technique for computed tomography (англ.) // Crystallography Reports. — 2013. — Vol. 58, iss. 7. — P. 1063-1066.

[17] Z.-H. Cho, J. P. Jones, M. Singh. Foundations of medical imaging (рус.). — Wiley New York, 1993.

[18] I. A. Kunina, S. A. Gladilin, D. P. Nikolaev. Blind compensation of radial distortion in a single image using fast Hough transform (англ.) // Computer Optics. — 2016. — Vol. 40, iss. 3. — P. 395-403.

[19] А. Мозговой. Преобразование Хафа в задачах автоматического распознавания рукописного текста (рус.). — 2012. — Вып. 9. — С. 62-64.

[20] E. Limonova, P. Bezmaternykh, D. Nikolaev, V. Arlazarov. Slant Rectiﬁcation in Russian Passport OCR System Using Fast HoughTransform (англ.) // 9-th International Conference on Machine Vision, ICMV 2016. — SPIE, 2017. — P. 103410P. — doi:10.1117/12.2268725.

[21] В. А. Фурсов, С. А. Бибиков, П. Ю. Якимов. Локализация контуров объектов на изображениях при вариациях масштаба с использованием преобразования Хафа (рус.) // Компьютерная оптика. — 2013. — Т. 37, вып. 4.

[22] R. Muniz, L. Junco, A. Otero. A robust software barcode reader using the Hough transform (англ.) // International Conference on Information Intelligence and Systems, 1999. Proceedings.. — IEEE, 1999. — P. 313-319.

[23] А. Рубис и др. Морфологическое сравнение по форме точечных паттернов и контурных изображений на основе преобразования Хафа и его модификаций (рус.) // Вестник компьютерных и информационных технологий. — 2011. — Вып. 7. — С. 9-16.

[24] М. Кудрина [и др.] Векторизация растровых изображений с использованием преобразования Хафа (рус.) // Труды Международного симпозиума "Надежность и качество". — 2013. — Т. 1.

[25] B. Vandame. Fast Hough transform for robust detection of satellite tracks (англ.) // Mining the Sky. — Springer, 2001. — P. 595-597.

[26] А. Семенов. Обнаружение радиолокационных целей с помощью преобразования Хафа (рус.) // Наука и образование: научное издание МГТУ им. НЭ Баумана. — 2014. — Вып. 12.

[27] B. Carlson, E. Evans, S. Wilson. Search radar detection and track with the Hough transform. III. Detection performance with binary integration (англ.) // IEEE transactions on Aerospace and Electronic Systems. — 1994. — Vol. 30, iss. 1. — P. 116-125.

[28] А. Долгий, А. Хатламаджиян. Гибридная модель интерпретации деформаций в балластной призме и основной площадке земляного полотна на основе целевого преобразования Хафа и нейронной сети Кохонена (рус.) // Известия Южного федерального университета. Технические науки. — 2007. — Т. 77, вып. 2.

[29] А. Дудкин, Д. Вершок, А. Селиханович. Выделение контуров на полутоновых изображениях топологических слоев интегральных микросхем (рус.) // Искусственный интеллект. — 2004. — Вып. 3. — С. 453-458.

[30] А. Григорьев, Т. Ханипов, Д. Николаев. Определение количества осей транспортного средства по видеоряду проезда (рус.) // 54-й научной конференции МФТИ. — 2011. — Т. 10. — С. 31.

[31] В. Гаганов, А. Игнатенко, М. Ломоносова. Трехмерная реконструкция плоских граней прозрачных минералов по набору изображений с микроскопа (рус.) // Труды конференции Графикон. — 2008. — С. 227-233.

[32] J. Skingley, A. Rye. The Hough transform applied to SAR images for thin line detection (англ.) // Pattern Recognition Letters. — 1987. — Vol. 6, iss. 1. — P. 61–67.