Байесовский подход в филогенетике

Теорема Байеса

Метафора, иллюстрирующая шаги метода MCMC

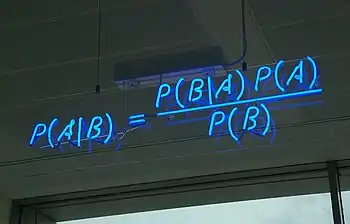
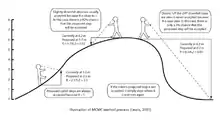
Байесовский подход является развитием вероятностного метода, разработанного английским математиком и священником Томасом Байесом на основе теоремы Байеса. Этот метод был опубликован в 1763 году[4], через два года после его смерти. Позднее современную формулировку теоремы вывел Пьер-Симон Лаплас[1] .

В 1953 году Николас Метрополис ввёл методы Монте-Карло для марковских цепей (MCMC, Markov chain Monte Carlo)[5]. Преимущества в скорости вычислений и возможность интеграции с методами MCMC позволили байесовскому подходу стать одним из самых популярных методов статистического вывода. Байесовский подход имеет множество применений в молекулярной филогенетике и систематике. По сравнению с другими методами построения филогенетических деревьев (метод максимальной экономии, метод максимального правдоподобия), он позволяет учитывать филогенетическую неопределенность, использовать априорную информацию и сложные модели эволюции, для которых традиционные методы имеют вычислительные ограничения.

Применение байесовского подхода в филогенетике состоит в следующем. Всё множество допустимых филогенетических деревьев ${\displaystyle T}$ описывается дискретными параметрами ${\displaystyle \tau }$ (топология деревьев) и непрерывными параметрами ${\displaystyle \alpha }$ (длины ветвей деревьев и параметры эволюционной модели замен). Чтобы вычислить значение апостериорной плотности распределения вероятностей ${\displaystyle f(T\mid B)}$ для дерева ${\displaystyle T}$ c топологией ${\displaystyle \tau _{0}}$ и параметрами ${\displaystyle \alpha _{0}}$, при заданных исходных данных ${\displaystyle B}$, применяется формула Байеса ${\displaystyle f(T(\tau _{0},\alpha _{0})\mid B)={\frac {f(B\mid T)f(T)}{P(B)}}}$, где ${\displaystyle f(B\mid T)}$ — условная плотность распределения вероятностей исходных данных ${\displaystyle B}$. Знаменатель в этой формуле вычисляется по формуле полной вероятности в виде суммы по ${\displaystyle \tau }$ интегралов от произведения ${\displaystyle f(T(\tau ,\alpha ))f(B\mid T(\tau ,\alpha ))}$ по ${\displaystyle \alpha }$, где ${\displaystyle f(T(\tau ,\alpha ))}$ — априорная плотность распределения для деревьев[6]. Явные аналитическое расчеты по этой формуле не всегда возможны, а численные — требуют большого количества вычислений при поиске максимума функции ${\displaystyle f(T\mid B)}$ по ${\displaystyle T}$. Применение метода статистических испытаний (который также называется методом Монте-Карло) на цепях Маркова позволяет получить приближенные значения апостериорных вероятностей и уменьшить вычислительную сложность алгоритма поиска наиболее вероятного дерева по критерию максимума апостериорной вероятности.

В методах MCMC апостериорная плотность вычисляется за счет имитации работы цепи Маркова, состояниями которой являются филогенетические деревья[2]. Расчет апостериорной плотности выполняется как частота посещения этих состояний в установившемся режиме. Наиболее вероятное дерево определяется по максимальной частоте того состояния, которое чаще всего посещается, или нескольких из них наиболее часто посещаемых. Методы MCMC можно описать двумя этапами: на первом применяется стохастический механизм для получения нового состояния цепи Маркова; на втором выполняется расчет вероятности перехода в это состояние и разыгрывается случайное событие смены состояния. Эта процедура повторяется тысячи или миллионы раз. Доля времени, в течение которого одиночное дерево посещается в процессе работы цепи Маркова, является достаточно точной аппроксимацией для его апостериорной вероятности. К числу наиболее часто применяемых алгоритмов, использующихся в методах MCMC, относятся алгоритм Метрополиса — Гастингса, алгоритм Метрополиса в сочетании с MCMC (MC³) и алгоритм LOCAL Ларгета и Симона.

Алгоритм Метрополиcа — Гастингса[7] является одним из наиболее распространенных методов MCMC и представляет собой модифицированную Гастингсом версию алгоритма Метрополиса[5]. Алгоритм Меторополиса — Гастингса строит случайную реализацию цепи Маркова, состояниями которой являются филогенетические деревья. При имитации изменения состояния на каждом шаге выполняется переход от одного дерева к другому за счет изменения топологии или параметров эволюционной модели по определённому правилу. Алгоритм состоит из следующих шагов[8]:

1. выбирается стартовое дерево ${\displaystyle Ti}$ со случайной топологией и параметрами модели и принимается как текущее;
2. строится дерево ${\displaystyle Tj}$ с новой топологией или новыми параметрами модели;
3. вычисляется отношение вероятностей (или функций плотности вероятности) нового дерева ${\displaystyle Tj}$ и старого дерева ${\displaystyle Ti}$: ${\displaystyle R={\frac {f(Tj)}{f(Ti)}}}$

(под ${\displaystyle f(T)}$ подразумевается условная вероятность или плотность распределения при заданных исходных данных ${\displaystyle B}$);

• если ${\displaystyle R\geqslant 1}$, то в качестве текущего дерева принимается новое дерево ${\displaystyle Tj}$;
• если ${\displaystyle R<1}$, то выбор дерева ${\displaystyle Tj}$ происходит с вероятностью ${\displaystyle R}$ (для этого генерируется случайное равномерно распределенное число в интервале ${\displaystyle (0,1)}$, и если это число меньше ${\displaystyle R}$, то в качестве текущего дерева принимается ${\displaystyle Tj}$, иначе остается ${\displaystyle Ti}$;

1. далее процесс повторяется с шага 2) n раз до тех пор, пока не достигнет равновесного распределения.

В оригинальном алгоритме Метрополиса предполагается, что вероятности переходов от дерева ${\displaystyle Tj}$ к дереву ${\displaystyle Ti}$ и обратно равны. Если это условие не выполняется, то применяются поправки Гастингса, состоящие в следующем: вероятность перехода вычисляется по формуле ${\displaystyle {\frac {f(Tj)}{f(Ti)}}{\frac {Q(Ti|Tj)}{Q(Tj|Ti)}}}$, где ${\displaystyle Q}$ — совместная функция распределения.

Алгоритм Метрополиса в сочетании с MCMC (Metropolis-coupled MCMC, MC³)[9], известный также как алгоритм параллельного отжига, является модифицированной версией алгоритма Метрополиса — Гастингса для марковских цепей со сложным и многомодальным распределением вероятностей состояний. Для этих случаев алгоритмы эвристического поиска деревьев критериями MP (метод максимальной экономии, maximum parsimony), ML (метод максимального правдоподобия) и ME (метод минимальной эволюции), а также МСМС могут выйти на локальный максимум, что приведёт к неверной аппроксимации апостериорной плотности распределения вероятностей. Алгоритм MC³ за счёт смешивания марковских цепей с разной температурой позволяет правильно аппроксимировать распределение апостериорных вероятностей и избегать попадания в локальные оптимумы.

Алгоритм параллельно запускает ${\displaystyle m}$ цепей, по ${\displaystyle n}$ итераций в каждой цепи с разными стационарными распределениями ${\displaystyle f_{j}(.)\ }$, ${\displaystyle j=1,2,\ldots ,m\ }$, где первое распределение с целевой плотностью ${\displaystyle f_{1}=f\ }$ называется холодной цепью, а другие цепи с распределениями ${\displaystyle f_{j}\ }$, ${\displaystyle j=2,3,\ldots ,m\ }$ называются разогретыми[10]. Плотности распределений разогретых цепей имеют вид:

${\displaystyle f_{j}(T)=f(T)^{1/[1+\lambda (j-1)]},\ \ \lambda >0,}$ где ${\displaystyle \lambda }$ — температурный фактор.

Возведение плотности ${\displaystyle f(.)}$ в степень ${\displaystyle 1/T\ }$ при ${\displaystyle T>1\ }$ имеет эффект уплощения распределения по аналогии с нагреванием металла. В таком распределении легче перемещаться между пиками, разделёнными долинами, чем в первоначальном распределении. После каждой итерации алгоритм предписывает выполнить обмен состояний между двумя случайно выбранными цепями с помощью предложенного Метрополисом шага. Обмен между состояниями ${\displaystyle i\ }$ и ${\displaystyle j\ }$ происходит с вероятностью:

${\displaystyle \alpha ={\frac {f_{i}(T^{(j)})f_{j}(T^{(i)})}{f_{i}(T^{(i)})f_{j}(T^{(j)})}}\ ,}$ где ${\displaystyle f^{(j)}\ }$ — текущее состояние в цепи с номером ${\displaystyle j\ }$, ${\displaystyle j=1,2,\ldots ,m\ }$[11].

Эвристически, разогретые цепи будут посещать локальные пики довольно легко, и обмен состояниями между цепями позволит холодной цепи иногда перепрыгивать через долины. Если ${\displaystyle f_{i}(T)/f_{j}(T)\ }$ слишком мало, обмен состояниями будет редко выполняться, поэтому в алгоритме используются несколько цепей с разными температурными факторами для улучшения смешивания[6].

Для получения стационарного распределения вероятностей используются только состояния из холодной цепи, а состояния из разогретых цепей отбрасываются.

Для генерации нового состояния марковской цепи существуют различные вероятностные способы модификации деревьев, например, бисекция с последующим переприсоединением, обмен ветвей, замена на ближнее соседнее дерево. Алгоритмы LOCAL[2] и GLOBAL[12] предлагают другой способ построения нового дерева по текущему за счёт изменения топологии и длин ветвей. Это приводит к значительному сокращению вычислений для больших деревьев по сравнению с алгоритмами бутстрэпа для методов максимального правдоподобия и максимальной экономии.

Общая идея заключается в том, что дерево представляется в виде следующих параметров: топология дерева и длина его ветвей, а также параметры модели замен. При изменении состояний марковской цепи выполняются последовательные шаги, в которых отдельно либо меняется топология дерева и длина его ветвей, либо меняются только параметры модели замен. Решение о переходе к новому дереву в качестве текущего состояния цепи Маркова принимается так же, как в алгоритме Метрополиса — Гастингса, но значение пороговой вероятности вычисляется с использованием параметров модифицированного дерева.

В алгоритме GLOBAL[12], представленном Мау, Ньютоном и Ларгетом в 1999 году, все длины ветвей дерева изменяются на небольшую величину в каждом цикле. Алгоритм Ларгета и Симона LOCAL[2] предполагает модификацию дерева в небольшой окрестности случайно выбранной внутренней ветви дерева.

Построение нового дерева в алгоритме LOCAL при модификации топологии и длин ветвей выполняется по следующему правилу: равновероятно выбирается произвольное внутреннее ребро дерева с вершинами ${\displaystyle u}$ и ${\displaystyle v}$. Вследствие того, что филогенетическое дерево должно быть бинарным, а ребро внутреннее, у каждой из вершин обязательно есть две смежные. Смежные вершины для ${\displaystyle u}$ произвольным образом обозначаются буквами ${\displaystyle a}$ и ${\displaystyle b}$, а смежные вершины для ${\displaystyle v}$ — буквами ${\displaystyle c}$ и ${\displaystyle d}$. Далее для вершин ${\displaystyle u}$ и ${\displaystyle v}$ равновероятно выбирается по одной смежной, например, ${\displaystyle a}$ и ${\displaystyle c}$, и рассматривается путь между вершинами ${\displaystyle a}$ и ${\displaystyle c}$, состоящий из трёх рёбер. Длины этих рёбер модифицируются пропорционально путём умножения на случайное число по правилу ${\displaystyle m^{\star }=m\exp(\lambda (U_{1}-0.5))\ }$, где ${\displaystyle m}$ — старая длина пути, ${\displaystyle m^{\star }}$ — новая длина пути, ${\displaystyle U_{1}\ }$ — это равномерно распредёленная случайная величина на отрезке ${\displaystyle (0,1)\ }$, а ${\displaystyle \lambda }$ — это положительный настраиваемый параметр. Следующий шаг модификации дерева состоит в отсоединении одной из вершин, ${\displaystyle u}$ или ${\displaystyle v}$, выбираемых равновероятно, и присоединения её в случайно выбранной по равномерному закону точке на пути от вершины ${\displaystyle a}$ до вершины ${\displaystyle c}$ вместе с её дочерней ветвью. При такой модификации возможно изменение топологии дерева, если порядок следования вершин ${\displaystyle u}$ и ${\displaystyle v}$ вдоль пути от ${\displaystyle a}$ к ${\displaystyle c}$ изменился, иначе — топология дерева не изменяется. Поправка Гастингса равна квадрату отношения длин нового и старого пути: ${\displaystyle (m^{\star }/m)^{2}}$.

При модификации параметров модели в алгоритме рассматриваются два варианта: в первом варианте, когда один параметр ограничен набором значений ${\displaystyle [0,M]}$, новое значение параметра вычисляется прибавлением равномерно распределённой случайной величины из интервала ${\displaystyle (-\delta ,\delta )}$. Если новое значение выходит за пределы допустимого диапазона ${\displaystyle [0,M]}$[2], то остаток отражается внутрь этого отрезка. Поправка Гастингса принимается равной 1. Второй вариант составляет случай, когда модифицируется множество параметров, сумма которых равна константе. В этом случае новое множество значений этих параметров выбирается из распределения Дирихле, центрированного по текущим значениям параметров. Поправка Гастингса вычисляется как отношение плотностей Дирихле с новыми и старыми параметрами.

• Значения бутстрэп против апостериорных вероятностей. Было показано, что значения бутстрэпа, вычисленные методами максимальной экономии или правдоподобия, обычно ниже, чем апостериорные вероятности, полученные байесовским методом[13]. Это приводит ряду вопросов, например: Приводят ли апостериорные вероятности к завышению вероятности результата? Являются ли значения бутстрэпа более устойчивыми по сравнению с апостериорными вероятностями?

• Выбор модели. Результаты Байесовского филогенетического анализа прямо коррелируют с выбранной моделью эволюции, поэтому важно выбрать модель, которая подходит наблюдаемым данным, иначе вывод о филогении может быть ошибочным. Многие ученые поднимали вопрос об интерпретации результатов байесовского анализа, когда модель неизвестна или неправильная. Например, слишком упрощенная модель может дать более высокие апостериорные вероятности[14][15] или простые модели связаны с большей неопределённостью, чем с той, которая вытекает из анализа бустрэпом.

MrBayes — это бесплатная программа, осуществляющая байесовский анализ филогении. Первоначально написана Джоном Хюльсенбеком и Фредериком Ронкустом в 2001 году[16]. Когда байесовские методы приобрели популярность, многие молекулярные филогенетики стали выбирать MrBayes. Программа использует стандартный алгоритм MCMC и алгоритм Метрополиса, связанный с MCMC.

MrBayes использует МСМС для приближённого вычисления апостериорных вероятностей деревьев[5]. Пользователь может поменять предположения о модели замен, априорных вероятностей и деталей МС анализа. Также программа позволяет удалять и добавлять таксоны и символы для анализа. В программе можно использовать широкий спектр моделей замен -- от стандартной модели подстановок DNA 4х4, также называемой JC69, в которой считается, что частоты оснований равны и все замены нуклеотидов происходят с равной вероятностью[17], до наиболее общей модели GTR, в которой различаются и частоты оснований, и вероятности замен. Также программа включает несколько 20х20 моделей замен аминокислот, кодоновые и дублетные модели замены ДНК. Программа предлагает различные методы для ослабления предположения о равных скоростях замен в нуклеотидных позициях[18]. MrBayes также может выводить наследственные состояния, содержащие неопределённость филогенетического дерева и параметров модели.

MrBayes 3[19] — это полностью реогранизованная и реконструированная версия первоначальной программы MrBayes. Главное новшество заключается в возможности программы приспосабливаться к неоднородности наборов данных. Такая структура позволяет пользователю смешивать модели и получать преимущество эффективности байесовского MCMC анализа, если он имеет дело с разными типами данных (например, белки, нуклеотиды, морфологические данные). По умолчанию программа использует алгоритм МСМС Метрополиса.

MrBayes 3.2 — это новая версия MrBayes, выпущенная в 2012 году[20]. Новая версия позволяет пользователю запускать несколько анализов параллельно. Также она обеспечивает более быстрое вычисление вероятностей и даёт возможность использования ресурсов графического процессора для выполнения этих вычислений. Версия 3.2 предоставляет больше опций для выходных данных, совместимых с программой FigTree и другими программами для просмотра деревьев.

Байесовский подход широко используется молекулярными филогенетиками для различных приложений:

• Вывод филогений[30][31]
• Вывод и оценка неопределенности филогений[32]
• Датирование с помощью молекулярного анализа[33]
• Вывод черт предковых форм[34][35]
• Вывод ареалов предковых форм[36]
• Модель динамики диверсификации и вымирания видов[37]
• Объяснение закономерностей распространения патогенных организмов[38]